7. Щелкните на кнопке ОК, чтобы открыть окно вывода.
3.5. Кластерный анализ (КА)
КА имеет определенное сходство с ДА; сходство заключается в том, что исследователь в обоих случаях ставит перед собой цель разделить совокупность объектов (а не переменных) на несколько более мелких групп. Тем не менее, процесс классификации в двух видах анализа принципиально различен. В КА объекты классифицируются на основе их различия без какой-либо предварительной информации о количестве и составе классов. В ДА количество и состав классов изначально задан, и основная задача заключается в определении того, насколько точно можно предсказать принадлежность объектов к классам при помощи данного набора дискриминантных переменных (предикторов).
Выделяют несколько этапов КА: 1) выбор переменных-критериев для кластеризации; 2) выбор способа измерения расстояния между объектами, или кластерами (изначально считается, что каждый объект соответствует одному кластеру); 3) формирование кластеров; 4) интерпретация результатов.
´Задача 3.6. Для решения требуется программа SPSS и файл данных KA . sav, который содержит данные о 16 подержанных кардиотренажерах «беговая дорожка» разных марок, выставленных на продажу. Провести КА объектов.
1. Откройте файл данных KA . sav.
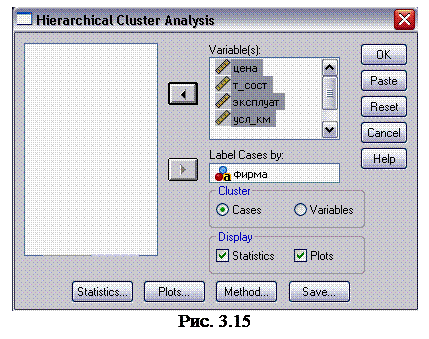
2. В меню Analyze (анализ) выберите команду Classify ► Hierarchical Cluster (Классификация ► иерархическая кластеризация). Откроется диалоговое окно Hierarchical Cluster Analysis (иерархический кластерный анализ) (рис. 3.15). Переменную фирма переместите в поле Label Cases by (Различать объекты по), а переменные цена – усл_км переместите в список Variable ( s ) (переменные).
3. Щелкните на кнопке Plots (диаграммы), чтобы открыть диалоговое окно Hierarchical Cluster Analysis : Plots (иерархический кластерный анализ: диаграммы) (рис. 3.16). Установите флажок Dendrogram (дендрограмма) и переключатель None (нет) в группе Icicle (диаграмма накопления). Щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Hierarchical Cluster Analysis (иерархический кластерный анализ).
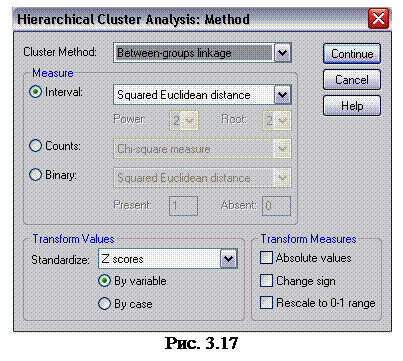4. Щелкните на кнопке Method (метод), чтобы открыть диалоговое окно Hierarchical Cluster Analysis : Method (иерархический кластерный анализ: метод) (рис. 3.17). В списке Cluster Method (метод кластеризации) оставьте выбранным пункт Between – groups linkage (межгрупповое связывание), в списке Standardize (стандартизация) выберите пункт Z score (z-шкала) и щелкните па кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Hierarchical Cluster Analysis (иерархический кластерный анализ).
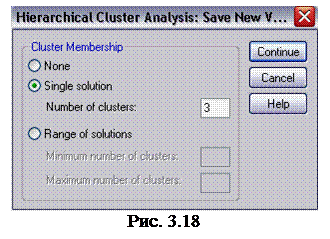
5. Щелкните па кнопке Save (сохранить), чтобы открыть диалоговое окно Hierarchical Cluster Analysis : Save New Variables (иерархический кластерный анализ: сохранение новых переменных) (рис.3.18). Установите переключатель Single Solution (заданное число кластеров), введите в расположенное рядом поле значение 3 и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Hierarchical Cluster Analysis (иерархический кластерный анализ).
6. Щелкните па кнопке ОК, чтобы открыть окно вывода.
Примечания: 1. В данном примере кластеризация осуществляется по следующим переменным: цена (стоимость), т_сост (экспертная оценка технического состояния по 10-балльной шкале), эксплуат (количество месяцев эксплуатации), усл_км (кол-во условных километров пробега с начала эксплуатации).
2. По умолчанию используется квадрат Евклидова расстояния, согласно которому расстояние между объектами равно сумме квадратов разностей между значениями одноименных переменных объектов. Предположим, что тренажер А имеет показатели технического состояния и эксплуатации 7 и 7, а тренажер В – 6 и 13. В этом случае расстояние между тренажерами вычисляется следующим образом: (7 – 6)2 + (7 – 13)2 = 37. При выполнении КА сумма квадратов разностей вычисляется для всех переменных. Получаемые расстояния используются программой при формировании кластеров. Помимо Евклидова существуют и другие виды расстояний. При необходимости обратитесь к руководству пользователя SPSS. Относительно вычисления расстояния может возникнуть следующий вопрос: будет ли адекватным результат КА в том случае, если переменные имеют различные шкалы измерения? Так, все переменные файла KA . sav имеют самые разные шкалы. Для решения проблемы шкалирования в SPSS используется стандартизация, в частности, ее простой метод – нормализация переменных, приводящая все переменные к стандартной z-шкале (среднее равно 0, стандартное отклонение – 1). Помимо одинаковой шкалы нормализованные переменные также имеют равные веса. В случае, если все исходные данные имеют одну и ту же шкалу измерения либо веса переменных по смыслу должны быть разными, стандартизацию переменных проводить не нужно.
3. Существует два основных метода формирования кластеров: метод слияния и метод дробления. В первом случае исходные кластеры увеличиваются путем объединения до тех пор, пока не будет сформирован единственный кластер, содержащий все данные. Метод дробления основан на обратной операции: сначала все данные объединяются в один кластер, который затем делится на части до тех пор, пока не будет достигнут желаемый результат. По умолчанию программой SPSS используется метод слияния, и мы рассмотрим его в этом разделе. В методе слияния предусмотрено несколько способов объединения объектов. Способ, применяемый по умолчанию, называется межгрупповым связыванием, или связыванием средних внутри групп. SPSS вычисляет наименьшее среднее значение расстояния между всеми парами групп и объединяет две группы, оказавшиеся наиболее близкими. На первом шаге, когда все кластеры представляют собой одиночные объекты, данная операция сводится к обычному попарному сравнению расстояний между объектами. Термин «среднее значение» приобретает смысл лишь на втором этапе, когда сформированы кластеры, содержащие более одного объекта. Так, в нашем примере на начальном этане имеется 16 кластеров (объектов); сначала в кластер объединяются два объекта с наименьшим расстоянием друг от друга. Затем подсчет расстояний повторяется, и в кластер объединяется еще одна пара переменных. На втором этапе вы получите либо 13 свободных объектов и 1 кластер, объединяющий 2 объекта, либо 11 свободных объектов и 2 кластера по 2 объекта в каждом. В конечном счете, все объекты окажутся в одном большом кластере. Существуют и другие методы объединения объектов. При необходимости обратитесь к руководству пользователя SPSS.
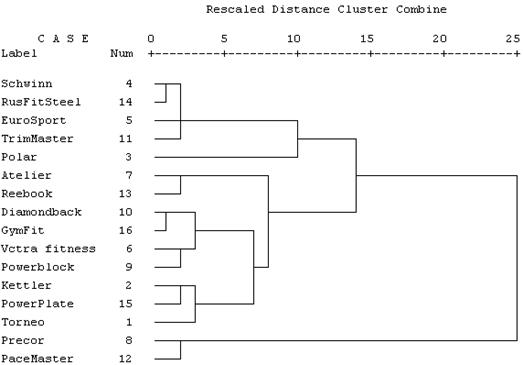
4. Как и в случае ФА, желаемое число кластеров и оценка результатов анализа зависят от целей исследователя. Для данного примера наиболее предпочтительно число кластеров, равное 3. Как показывает анализ, все тренажеры можно разделить на 3 группы: 1-я группа (на дендрограмме занимает центральное положение) имеет среднюю стоимость (среднее значение – 11883), небольшой срок эксплуатации (8 мес) и низкий условный километраж (3139 км). 2-я группа (на дендрограмме – вверху) имеет низкую стоимость (8750), небольшой пробег, наибольший возраст, не высокое техническое состояние (6). 3-я группа (на дендрограмме – внизу) содержит дорогие модели с небольшим сроком эксплуатации и изношенности, высоким баллом технического состояния.
´Задача 3.7 [7]. Для решения требуется программа SPSS и файл данных DA - FA - KA . sav. В этой задаче проводится КА, в котором вместо объектов участвуют переменные и1 – и11.
Обычно при группировании переменных исследователя интересует их взаимосвязь, а не их различие (сходство), как при группировании объектов. Исключением является случай, когда данные представляют собой оценки объектов экспертами, в этом случае строки соответствуют экспертам, а столбцы – оцениваемым объектам. Поскольку в нашем примере интерес представляют именно взаимосвязи между переменными и мы хотим сравнить результаты с ФА, то в качестве меры близости целесообразно выбрать корреляцию. При этом корреляции надо учитывать по абсолютной величине, так как большие (по модулю) отрицательные их величины так же свидетельствуют о связи, как и большие положительные. Все это необходимо иметь в виду, если речь идет о кластеризации переменных. Большинство остальных параметров команды оставим установленными по умолчанию; даже в стандартизации в данном случае нет необходимости, так как на величину корреляции не влияют единицы измерения переменных. Добавим лишь дендрограмму в выводимые результаты и исключим оттуда диаграмму накопления.
1. Откройте файл данных DA - FA - KA . sav.
2. 
В меню Analyze (анализ) выберите команду Classify ► Hierarchical Cluster (классификация ► иерархическая кластеризация). Откроется диалоговое окно Hierarchical Cluster Analysis (иерархический кластерный анализ) (рис.3.19). В группе Cluster (кластеризация) установите переключатель Variables (переменные). Переместите переменные и1 – и11 в список Variable ( s ) (переменные).
3. Щелкните на кнопке Plots (диаграммы), чтобы открыть диалоговое окно Hierarchical Cluster Analysis : Plots (иерархический кластерный анализ: диаграммы) (рис. 3.16). Установите флажок Dendrogram (дендрограмма) и переключатель None (нет) в группе Icicle (диаграмма накопления). Щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Hierarchical Cluster Analysis (иерархический кластерный анализ).
4. 
Щелкните на кнопке Method (метод), чтобы открыть диалоговое окно Hierarchical Cluster Analysis : Method (иерархический кластерный анализ: метод) (рис. 3.20). В списке Interval (интервал) выберите пункт Pearson correlation (корреляция Пирсона), а в группе Transform Measures (преобразование значений) установите флажок Absolute values (абсолютные значения). Щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Hierarchical Cluster Analysis (иерархический кластерный анализ).
5. Щелкните на кнопке ОК, чтобы открыть окно вывода.
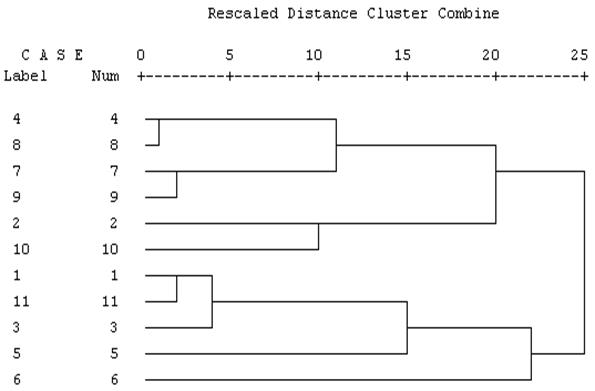
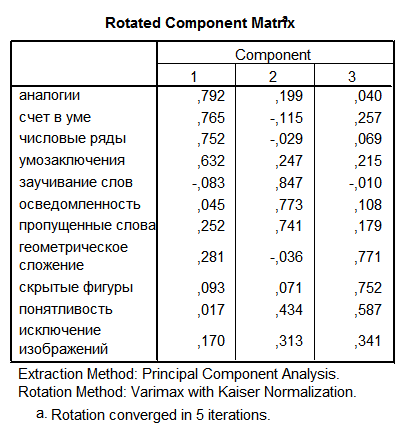
Сравните результаты КА и ФА, изображенные выше (см. файл DA - FA - KA . sav).
3.6. Многомерное шкалирование (МШ)
Основное достоинство МШ – представление больших массивов данных о различии объектов в графическом виде. При МШ матрица различий между объектами (вычисленными, например, по их экспертным оценкам) представляется в виде одно-, двух– или трех– и более мерного графического изображения взаимного расположения этих объектов. Если две точки на изображении удалены друг от друга, то между соответствующими объектами имеется значительное расхождение; напротив, близость точек говорит о сходстве объектов.
МШ имеет много общих черт с ФА. Так же, как и при ФА, создается система координат пространства, в котором определяется расположение точек. Так же, как и при ФА, происходит снижение размерности и упрощение данных. Однако при ФА обычно используются коэффициенты корреляции, а при МШ – меры различия между объектами. Наконец, в ФА наибольший интерес вызывают углы между точками, представляющими данные, а в МШ ключевой величиной является расстояние между этими точками.
Помимо факторного анализа МШ имеет несколько общих черт с КА (см. раздел 3.5). В обоих случаях анализируется расстояние между объектами; однако при КА типичной является количественная процедура объединения объектов в группы (кластеры), а при МШ качественный анализ объектов проводится визуально с помощью диаграммы.
Процедура ММШ SPSS, имеющая историческое название ALSCAL, фактически не является одной программой, а представляет собой набор небольших процедур, каждая из которых соответствует своему типу данных. В этом разделе будут приведены несколько примеров для различных типов данных.
В первом примере будет обработана социограмма для группы учащихся; здесь их количественные оценки отношений друг к другу будут преобразованы в графическое изображение взаимного расположения учащихся.
Во втором примере будут рассмотрены результаты тестирования учащихся по пяти показателям и графически представлены различия между учащимися на плоском изображении.
Наконец, третий пример будет представлять собой небольшое исследование восприятия и понимания студентами пяти многомерных методов статистического анализа.
´Задача 3.8 [7]. Для решения требуется программа SPSS и файл данных MDS -1. sav. Квадратная асимметричная матрица различий. Преподаватель решил создать идеальную психологическую обстановку в группе во время занятия, рассадив учащихся так, чтобы ни один из них не оказался рядом с тем, кто ему не нравится. Для этого каждому из 12 студентов было предложено оценить степень своей симпатии к своим однокурсникам по пятибалльной шкале (от 1 до 5, где 1 – максимум симпатии, а 5 – максимум антипатии). Результатом МШ будет диаграмма, на которой удаленность точек будет соответствовать отношениям между учащимися.
Вначале необходимо создать квадратную (12 × 12) матрицу различий. Позже на основе этой матрицы будет построено двухмерное изображение, иллюстрирующее взаимоотношения студентов. В ходе МШ исходная матрица 12 × 12 преобразуется в гораздо более простую матрицу 12 × 2 (где 2 – число измерений), содержащую координаты точек для изображения. Исходную матрицу называют квадратной асимметричной матрицей различий. Пояснения, что означают составляющие это определение термины, даны в конце настоящего раздела.
1. Откройте файл данных MDS -1. sav . В меню Analyze (анализ) выберите команду Scale ► Multidimensional Scaling (шкалирование ► многомерное шкалирование). Откроется диалоговое окно Multidimensional Scaling (многомерное шкалирование). После выполнения предыдущего шага у Вас должно быть открыто диалоговое окно Multidimensional Scaling (многомерное шкалирование). Переместите переменные с1 – с12 в список Variables (переменные) (рис. 3.21).
2. Щелкните на кнопке Shape (форма), чтобы открыть диалоговое окно Multidimensional Scaling : Shape Of Data (многомерное шкалирование: форма данных). Установите переключатель Square asymmetric (квадратная асимметричная) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.22).
3. Щелкните на кнопке Model (модель), чтобы открыть диалоговое окно Multidimensional Scaling : Model (многомерное шкалирование: модель). В группе Conditionality (условие) установите переключатель Row (строка) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.23).
4. Щелкните на кнопке Options (параметры), чтобы открыть диалоговое окно Multidimensional Scaling : Options (многомерное шкалирование: Параметры). Установите флажок Croup plots (групповые диаграммы) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.24).