Классификация методов по исходным предположениям о структуре данных
1. Методы, исходящие из предположения о согласованной изменчивости признаков, измеренных у множества объектов. На корреляционной модели основаны ФА, МР, отчасти – ДА.
2. Методы, исходящие из предположения о том, что различия между объектами можно описать как расстояние между ними. На дистантной модели основаны КА и МШ, частично – ДА. МШ и ДА подтверждают предположение о том, что исходные различия между объектами можно представить как расстояния между ними в пространстве небольшого числа шкал (функций).
Классификация методов по виду исходных данных
1. Методы, использующие в качестве исходных данных только признаки, измеренные у группы объектов (МР, ДА и ФА).
2. Методы, исходными данными для которых могут быть попарные сходства (различия) между объектами (КА и МШ). МШ, кроме того, может анализировать данные о попарном сходстве между совокупностью объектов, оцененном группой экспертов. При этом совместно анализируются как различия между объектами, так и индивидуальные различия между экспертами.
3.2. Множественный регрессионный анализ (МР)
МР предназначен для изучения взаимосвязи одной переменной (зависимой) и нескольких других переменных (независимых) в интересах предсказания некоторого результата или существенности влияния той или иной переменной на предсказываемый результат.
Исходные данные для МР представляют собой матицу «объект-признак».
Связь одной переменной (зависимой) Y и нескольких других переменных (независимых) Xn выражают линейным уравнением
y = b 0 + b1 x1 + b2 x2+ … + bn xn+ e,
где: y – зависимая переменная; x 1, 2 … n – независимые переменные; b 1, 2 … n – параметры модели; e – ошибка предсказания.
 Качественным аналогом МР является ДА (см. разд. 3.2).
Качественным аналогом МР является ДА (см. разд. 3.2).
Условия получения приемлемых результатов МР
Регрессия, как и корреляция, анализирует линейные зависимости. Ранее была рассмотрена процедура оценки криволинейных зависимостей в контексте простого регрессионного анализа. Если теория или статистический расчет показывает, что между критерием и одним или несколькими предикторами существует криволинейная зависимость, то можно применить процедуру линеаризации.
Основные условия применения МРА:
1. Исследование должно быть продумано по форме и исполнению. Анализ регрессии для не связанных по смыслу величин приводит к бесполезным результатам.
2. Объем выборки желательно иметь n ≥ 50.
3. Данные должны быть корректными и записаны в таблицу без ошибок.
4. Распределение значений предикторов должно быть близким к нормальному (значения асимметрий и эксцессов по модулю не превосходят 1).
5. Нормальность распределения зависимой переменной также желательна, однако допустимы как отклонения от нормальности, так и использование дискретных переменных с малым числом значений.
6. Наиболее жестким требованием является запрет на использование независимых переменных, корреляции между которыми близки к 1 (-1). Поэтому перед проведением регрессионного анализа никогда не бывает лишним вычисление корреляций между предикторами.
7. Не желательно задействовать предикторы, совпадающие по смыслу.
´Задача 3.1 [7]. Для решения требуется программа SPSS и файл данных MR . sav. Число объектов в файле данных MR . sav n = 46. Переменные файла, которые мы будем использовать: помощь – зависимая переменная, интерпретируемая как время (в секундах) оказания помощи партнеру (среднее – 30, стандартное отклонение – 10); симпатия – оценка своей симпатии к партнеру, нуждающемуся в помощи (по 20-балльной шкале); агрессия – оценка своей агрессивности к партнеру (по 20-балльной шкале); польза – оценка пользы от своей помощи (по 20-балльной шкале); проблема – оценка серьезности проблемы своего партнера (по 20-балльной шкале); эмпатия – оценка эмпатии (склонности к сопереживанию) как результат тестирования (по 10-балльной шкале).
1. Запустите программу SPSS. После выполнения этого шага на экране появится окно редактора данных SPSS. Откройте файл данных MR . sav, выполнив следующие действия: выберите в меню File (файл) команду Open ► Data (открыть ►данные) или щелкните на кнопке Open File (открыть файл) панели инструментов. В открывшемся диалоговом окне дважды щелкните на имени MR . sav или введите его с клавиатуры и щелкните па кнопке ОК.
2. В меню Analyze (анализ) выберите команду Regression ► Linear (регрессия ► линейная). На экране появится диалоговое окно Linear Regression (линейная регрессия) (рис. 3.1).
3. Щелкните сначала на переменной помощь, чтобы выделить се, а затем – на верхней кнопке со стрелкой, чтобы переместить переменную в поле Dependent (зависимая переменная). Выделите переменные симпатия, проблема, эмпатия, польза и агрессия, затем переместите их в список Independent ( s ) (независимые переменные).
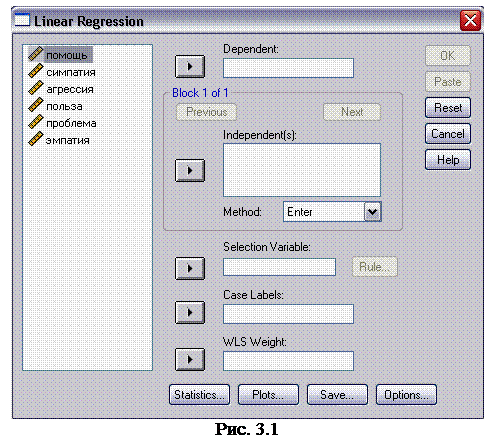 4. В раскрывающемся списке Method (метод) выберите пункт Forward (прямой). Щелкните на кнопке ОК, чтобы открыть окно вывода.
4. В раскрывающемся списке Method (метод) выберите пункт Forward (прямой). Щелкните на кнопке ОК, чтобы открыть окно вывода.
5. В результате программа сгенерирует данные, показывающие, какая из независимых переменных оказывает наибольшее влияние на зависимую переменную. Метод Forward (прямой) обеспечит включение в уравнение регрессии всех предикторов, имеющих значимую частную корреляцию с критерием β в порядке убывания значимости.
 ´Задача 3.2 [7]. Для решения требуется программа SPSS и файл данных MR . sav.
´Задача 3.2 [7]. Для решения требуется программа SPSS и файл данных MR . sav.
1. Откройте диалоговое окно Linear Regression (линейная регрессия), показанное на рис. 3.1. Если Вы уже успели поработать с этим окном, очистите его щелчком на кнопке Reset (сброс) и выполните следующие действия.
 2. Щелкните сначала на переменной помощь, чтобы выделить се, а затем – на верхней кнопке со стрелкой, чтобы переместить переменную в поле Dependent (зависимая переменная). Выделите переменные симпатия, проблема, эмпатия, польза и агрессия, затем переместите их в список Independent ( s ) (независимые переменные).
2. Щелкните сначала на переменной помощь, чтобы выделить се, а затем – на верхней кнопке со стрелкой, чтобы переместить переменную в поле Dependent (зависимая переменная). Выделите переменные симпатия, проблема, эмпатия, польза и агрессия, затем переместите их в список Independent ( s ) (независимые переменные).
3. В раскрывающемся списке Method (метод) выберите пункт Stepwise (по шагам).
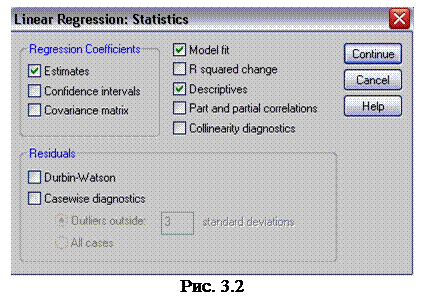
 4. Щелкните па кнопке Statistics (статистики), чтобы открыть диалоговое окно Linear Regression : Statistics (линейная регрессия: статистики), (рис. 3.2). Установите флажок Descriptives (описательные статистики) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Linear Regression (линейная регрессия).
4. Щелкните па кнопке Statistics (статистики), чтобы открыть диалоговое окно Linear Regression : Statistics (линейная регрессия: статистики), (рис. 3.2). Установите флажок Descriptives (описательные статистики) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Linear Regression (линейная регрессия).
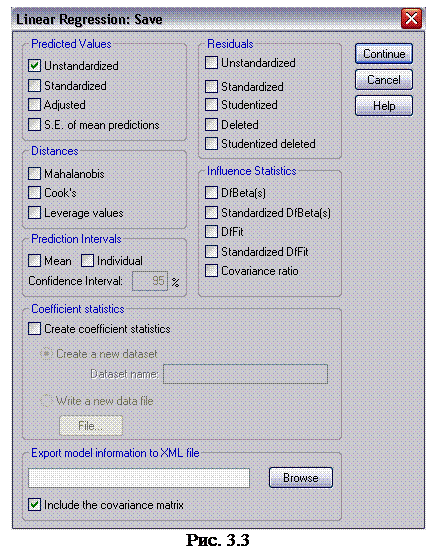
5. Щелкните па кнопке Save (сохранение), чтобы открыть диалоговое окно Linear Regression : Save (линейная регрессия: сохранение) (рис. 3.3). Установите флажок Unstandardized (нестандартизированные значения) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Linear Regression (линейная регрессия).
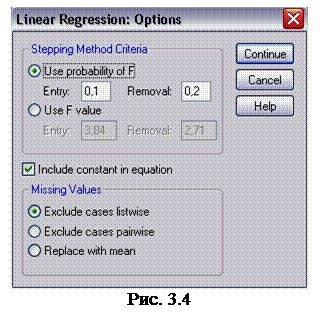
6. Щелкните на кнопке Options (параметры), чтобы открыть диалоговое окно Linear Regression : Options (линейная регрессия: параметры), показанное на рис. 3.4. В поле Entry (включение) введите значение 0,1, в поле Removal (удаление) введите значение 0,2 и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Linear Regression (линейная регрессия).
7. Щелкните на кнопке ОК, чтобы открыть окно вывода.
В результате выполнения приведенных инструкций будут сгенерированы данные, позволяющие судить о том, какая из независимых переменных оказывает наибольшее влияние на критерий.
На основе этих данных можно составить уравнение регрессии:
(помощь) = – 5 ,315 + 1,257 (польза) + 1,168 (агрессия) + 1,033(симпатия).
3.3. Дискриминантный анализ (ДА)
 ДА позволяет предсказать принадлежность объектов к двум или более непересекающимся группам.
ДА позволяет предсказать принадлежность объектов к двум или более непересекающимся группам.
 Исходными данными для ДА является множество объектов, разделенных на группы так, что каждый объект может быть отнесен только к одной группе. Допускается при этом, что некоторые объекты не относятся ни к какой группе (являются «неизвестными»). Для каждого из объектов имеются данные по ряду количественных переменных. Такие переменные называются дискриминантными переменными, или предикторами.
Исходными данными для ДА является множество объектов, разделенных на группы так, что каждый объект может быть отнесен только к одной группе. Допускается при этом, что некоторые объекты не относятся ни к какой группе (являются «неизвестными»). Для каждого из объектов имеются данные по ряду количественных переменных. Такие переменные называются дискриминантными переменными, или предикторами.
Задачами ДА является определение: 1) решающих правил, позволяющих по значениям предикторов отнести каждый объект (в том числе и «неизвестный») к одной из известных групп; 2) «веса» каждого предиктора для разделения объектов на группы.
ДА основан на составлении уравнения регрессии, использующего номинативную зависимую переменную.
Этапы ДА
ДА состоит из четырех основных этапов.
1. Выбор переменных-предикторов. Исследователь использует свои теоретические знания, практический опыт, догадки и т. п. для того, чтобы составить список переменных, которые могут повлиять на результат группировки (переменную-критерий).
2. Обычно на начальном этапе ДА для предикторов формируется корреляционная матрица. В данном контексте она имеет особый смысл, называется общей внутригрупповой корреляционной матрицей и содержит средние коэффициенты корреляции для двух или более корреляционных матриц (каждая для одной группы). Помимо общей внутригрупповой корреляционной матрицы можно также вычислить ковариационные матрицы для отдельных групп, для всей выборки либо общую внутригрупповую ковариационную матрицу. Нередко исследователи применяют серию t-критериев между двумя группами для каждой переменной либо однофакторный дисперсионный анализ, если число групп оказывается больше двух. Поскольку целью дискриминантного анализа является составление наилучшего уравнения регрессии, дополнительный анализ исходных данных никогда не является лишним.
 3. Выбор параметров. В этом разделе будет продемонстрирован один из методов ДА. По умолчанию программа реализует метод, который основан на принудительном включении в регрессионное уравнение всех предикторов, указанных исследователем. В нашем случае используется метод Уилкса (Wilks), относящийся к категории пошаговых методов и основанный на минимизации коэффициента Уилкса (λ) после включения в уравнение регрессии каждого нового предиктора.
3. Выбор параметров. В этом разделе будет продемонстрирован один из методов ДА. По умолчанию программа реализует метод, который основан на принудительном включении в регрессионное уравнение всех предикторов, указанных исследователем. В нашем случае используется метод Уилкса (Wilks), относящийся к категории пошаговых методов и основанный на минимизации коэффициента Уилкса (λ) после включения в уравнение регрессии каждого нового предиктора.
4. Интерпретация результатов. Целью ДА является составление уравнения регрессии с использованием выборки, для которой известны значения и предикторов, и критерия. Это уравнение позволяет по известным значениям предикторов определить неизвестные значения критерия для другой выборки. Разумеется, точность рассчитываемых значений критерия для второй выборки в общем случае не выше, чем для исходной. Так, в нашем примере регрессионное уравнение обеспечило около 90% корректных результатов для той выборки, с помощью которой оно было создано. Соответственно, точность предсказания успешности обучения для 10 абитуриентов может достигать 90% лишь в том случае, если выборка претендентов совершенно идентична тем 46 учащимся, данные для которых послужили основой для прогноза.
´Задача 3.3 [7]. Для решения требуется программа SPSS и файл данных DA - FA - KA . sav. Файл DA - FA - KA . sav содержит данные о 46 учащихся (объекты с 1-го по 46-й), закончивших курс обучения, в отношении которых известны оценки успешности обучения: «зачет» – 1, «незачет» – 0. Кроме того, в файл включены данные предварительного тестирования этих учащихся до начала обучения (13 переменных):
► и1, и2, ..., и11 – показатели теста интеллекта;
► э_и – показатель экстраверсии по тесту Г. Айзенка;
► н – показатель нейротизма по тесту Г. Айзенка.
 Для 10 абитуриентов (объекты с 47-го по 56-й) известны лишь результаты их предварительного тестирования (13 перечисленных переменных). Значения переменной оценка для них еще неизвестны и в файле данных им соответствуют пустые ячейки. Требуется спрогнозировать успешность обучения 10 абитуриентов на основе предварительного тестирования в предположении, что выборки закончивших обучение и абитуриентов идентичны.
Для 10 абитуриентов (объекты с 47-го по 56-й) известны лишь результаты их предварительного тестирования (13 перечисленных переменных). Значения переменной оценка для них еще неизвестны и в файле данных им соответствуют пустые ячейки. Требуется спрогнозировать успешность обучения 10 абитуриентов на основе предварительного тестирования в предположении, что выборки закончивших обучение и абитуриентов идентичны.
1. Откройте файл данных DA - FA - KA . sav.
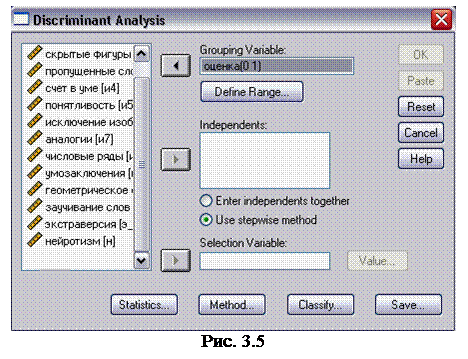
2. В меню Analyze (анализ) выберите команду Classify ► Discriminant (классификация > дискриминантный анализ). На экране появится диалоговое окно Discriminant Analysis (дискриминантный анализ) (рис. 3.5).
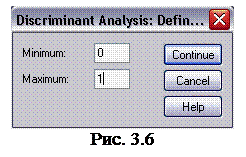 3. Переместите переменную оценка в поле Grouping Variable (группирующая переменная). Щелкните па кнопке Define Range (задать диапазон), чтобы открыть диалоговое окно Discriminant Analysis : Define Range (дискриминантный анализ: Задание диапазона) (рис. 3.6). В поле Minimum (минимум) введите значение 0, в поле Maximum (максимум), введите значение 1 и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Discriminant Analysis (дискриминантный анализ).
3. Переместите переменную оценка в поле Grouping Variable (группирующая переменная). Щелкните па кнопке Define Range (задать диапазон), чтобы открыть диалоговое окно Discriminant Analysis : Define Range (дискриминантный анализ: Задание диапазона) (рис. 3.6). В поле Minimum (минимум) введите значение 0, в поле Maximum (максимум), введите значение 1 и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Discriminant Analysis (дискриминантный анализ).
4. Переменные от и1 до н переместите в список Independents (независимые переменные), установите переключатель Use stepwise method (использовать пошаговый метод).
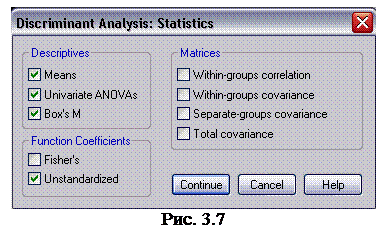
5. Щелкните на кнопке Statistics (статистики), чтобы открыть диалоговое окно Discriminant Analysis : Statistics (дискриминантный анализ: статистики) (рис. 3.7). Установите флажки Means (средние), Box ' s M (М Бокса), Univariate ANOVAs (однофакторный дисперсионный анализ), Unstardardized (нестандартизированные коэффициенты) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Discriminant Analysis (дискриминантный анализ).
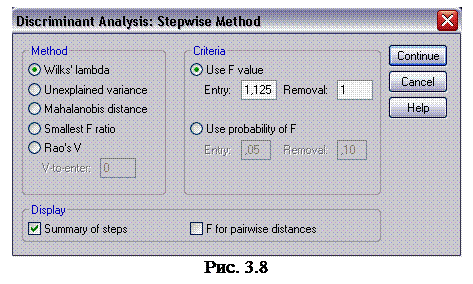
 6. Щелкните па кнопке Method (метод), чтобы открыть диалоговое окно Discriminant Analysis : Stepwise Method (дискриминантный анализ: пошаговый метод) (рис. 3.8). В поле Entry (ввод), введите значение 1,125, в поле Removal (вывод), введите значение 1 и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Discriminant Analysis (дискриминантный анализ).
6. Щелкните па кнопке Method (метод), чтобы открыть диалоговое окно Discriminant Analysis : Stepwise Method (дискриминантный анализ: пошаговый метод) (рис. 3.8). В поле Entry (ввод), введите значение 1,125, в поле Removal (вывод), введите значение 1 и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Discriminant Analysis (дискриминантный анализ).
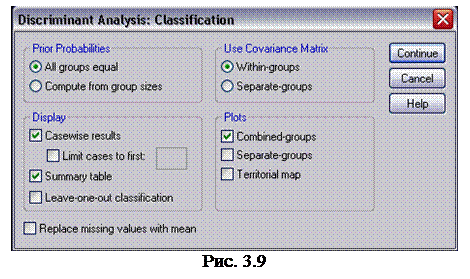 7. Щелкните на кнопке Classify (классификация), чтобы открыть диалоговое окно Discriminant Analysis : Classification (дискриминантный анализ: классификация) (рис. 3.9). Установите флажки Casewise results (результаты для объектов), Summary table (итоговая таблица) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Discriminant Analysis (дискриминантный анализ).
7. Щелкните на кнопке Classify (классификация), чтобы открыть диалоговое окно Discriminant Analysis : Classification (дискриминантный анализ: классификация) (рис. 3.9). Установите флажки Casewise results (результаты для объектов), Summary table (итоговая таблица) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Discriminant Analysis (дискриминантный анализ).
8. Щелкните на кнопке ОК, чтобы открыть окно вывода.
В результате выполнения приведенных инструкций будут сгенерированы коэффициенты (Canonical Discriminant Function Coefficients) для группировки интересующих нас объектов в целях прогнозирования: На основе этих данных можно составить уравнение регрессии
(0/1) = – 9,865 + 0,382 (счет в уме) – 0,241 (умозаключения) +
+ 0,214 (понятливость) + 0,185 (аналогии) + 0,162 (скрытые фигуры) +
+ 0,157 (заучивание слов) + 0,097 (экстраверсия)
или
(0/1) = – 9,865 + 0,382 (и4) – 0,241 (и9) + 0,214 (и5) + 0,185 (и7) + 0,162 (и2) + 0,157 (и11) + 0,097 (э_и).
3.4. Факторный анализ (ФА);
За последние 30–40 лет ФА приобрел значительную популярность в психологических и социальных исследованиях. Во многом этому способствовала разработка Раймондом Кеттеллем знаменитого 16-факторного личностного опросника (16PF). Именно при помощи ФА ему удалось свести около 4500 наименований личностных особенностей к 187 вопросам, которые, в свою очередь, позволяют измерить 16 различных свойств личности.
ФА дает возможность количественно определить латентные переменные, которые непосредственно измерить невозможно, исходя из нескольких доступных измерению явных переменных. Например, явные характеристики «посещает развлекательные мероприятия», «много разговаривает», «охотно идет на контакт с любым незнакомым человеком» могут служить оценками латентного качества «общительность», которое непосредственно не поддается количественному измерению. ФА позволяет выделить для большого числа признаков сравнительно узкий набор «свойств», объединяющих более тесно связанные признаки в группы и называемые факторами.
Процедура ФА состоит из четырех основных стадий:
1. Вычисление корреляционной матрицы для всех переменных, участвующих в анализе.
2. Извлечение факторов.








