Ранговый коэффициент корреляции Спирмена
Формула для вычисления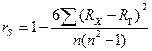 
.
´Задача 2.27. Какова корреляция между рангом рождения и СБ осенним для людей, отработавших 20 и менее часов? Ранг рождения – это порядковая переменная, поэтому необходимо использовать формулу Спирмена. Выберите записи с числовыми значениями 20 или менее из графы Отработанные часы. Впишите номера испытуемых в первый столбец, а СБ осенний (XI) – во второй. Расположите часы в порядке возрастания и впишите данные по рангу СБ (Rx) и рангу рождения (RY) в столбцы 3 и 4. Определите разность между рангом СБ и рангом рождения (Rx – RY), возведите в квадрат каждую разность: (Rx – RY)2, а затем сложите полученные результаты Σ(RX – RY)2. Подставьте эти величины в формулу.
| X1 | X5 | X3 | |||
| Номер | СБ осенний | Ранг СБ | Ранг рождения | (Rx – Ry) | (Rx – RY)2 |
| XI | Rx | Ry | |||
| 2 | 4,6 | 1 | 3 | –2 | 4 |
| 3 | 4,7 | 2 | 2 | 0 | 0 |
| 5 | 5,0 | 4 | 1 | 3 | 9 |
| 9 | 4,6 | 1 | 2 | –1 | 1 |
| 10 | 4,9 | 3 | 1 | 2 | 4 |
| 11 | 5,0 | 4 | 2 | 2 | 4 |
| 16 | 4,9 | 3 | 1 | 2 | 4 |
| 17 | 4,7 | 2 | 3 | –1 | 1 |
| n = 8 | Σ(RX – RY)2 = 27 |
.
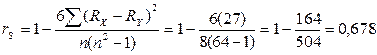По табл. П 3.1 определяем статистическую значимость r, найдя критическое значение. В нашем примере rS = 0,678, а n = 8. Выбрав уровень значимости р = 0,05, мы видим, что в нашем случае величина rS не достигает критического значения 0,738 и, следовательно, он не является статистически значимым, что неудивительно, принимая во внимание ограниченное число наблюдений.
Коэффициент корреляции Пирсона
Еще один часто используемый коэффициент корреляции, называемый коэффициентом корреляции Пирсона (r), используется для измерения связи между двумя переменными на интервальных шкалах. Используется только в случае линейной зависимости. Формула для приблизительного вычисления r.
.
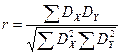´Задача 2.28. Какова корреляция между количеством отработанных часов (X 7) и СБ осенним (X 5) испытуемого? Начните анализ с построения столбцов для номера, СБ (Xi) и отработанных часов (Yi). Далее найдите отклонения DX и DY , затем квадраты отклонений D X2 и D Y2. Затем вычислите суммы квадратов отклонений Σ D X2 и Σ D Y2, а также сумму произведений отклонений Σ DXDY.
| X1 | X5 | X7 |
|
| |||
| № | СБ | Отработанные часы |
|
| |||
| Xi | Yi | DX | DY | D X 2 | D Y 2 | DXDY | |
| 1 | 3,9 | 38,0 | –0,5 | 14,5 | 0,3 | 209,4 | –7,5 |
| 2 | 4,6 | 15,0 | 0,2 | –8,5 | 0,0 | 72,8 | –1,6 |
| 3 | 4,7 | 10,0 | 0,3 | –13,5 | 0,1 | 183,0 | –3,8 |
| 4 | 4,2 | 30,0 | –0,2 | 6,5 | 0,0 | 41,9 | –1,4 |
| 5 | 5,0 | 12,0 | 0,6 | –11,5 | 0,3 | 132,9 | –6,7 |
| 6 | 3,7 | 35,0 | –0,7 | 11,5 | 0,5 | 131,6 | –8,2 |
| 7 | 3,7 | 30,0 | –0,7 | 6,5 | 0,5 | 41,9 | –4,6 |
| 8 | 4,4 | 30,0 | 0,0 | 6,5 | 0,0 | 41,9 | –0,1 |
| 9 | 4,6 | 20,0 | 0,2 | –3,5 | 0,0 | 12,5 | –0,6 |
| 10 | 4,9 | 10,0 | 0,5 | –13,5 | 0,2 | 183,0 | –6,5 |
| 11 | 5,0 | 20,0 | 0,6 | –3,5 | 0,3 | 12,5 | –2,1 |
| 12 | 4,0 | 35,0 | –0,4 | 11,5 | 0,2 | 131,6 | –4,8 |
| 13 | 4,6 | 30,0 | 0,2 | 6,5 | 0,0 | 41,9 | 1,2 |
| 14 | 4,2 | 30,0 | –0,2 | 6,5 | 0,0 | 41,9 | –1,4 |
| 15 | 4,0 | 35,0 | –0,4 | 11,5 | 0,2 | 131,6 | –4,8 |
| 16 | 4,9 | 10,0 | 0,5 | –13,5 | 0,2 | 183,0 | –6,5 |
| 17 | 4,7 | 10,0 | 0,3 | –13,5 | 0,1 | 183,0 | –3,8 |
| n = 17 | 4,4 | 23,5 | 0,0 | 0,0 | 3,3 | 1776,2 | –63,4 |
Полученные значения подставьте в формулу
.
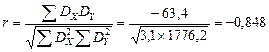Примечание. Знак «минус» перед коэффициентом корреляции отражает направление связи, а не значение. В данном случае зависимость обратная – чем больше человек занимается, тем ниже его СБ осенний (естественно, это шуточный пример). Чтобы найти уровень значимости для r , нам необходимо подсчитать степени свободы, или df = ( n – 2), а затем обратиться к табл. П 3.2. Имея df = 15 и используя уровень значимости 0,05, мы можем определить, превышает ли полученная нами величина r = 0,846 критическое значение, приведенное в таблице. Критическое значение равно 0,456 и меньше полученной нами величины 0,846; таким образом, между количеством отработанных часов и СБ осенним имеет место статистически значимая отрицательная корреляция.
Регрессионно-корреляционный анализ
Графическое решение задачи выявляет регрессию (форму зависимости) и уравнение связи. Линейная зависимость описывается уравнением
y = a + bx ,
где: а и b – коэффициенты, определяемые по формулам:
a = y – bx ,
.
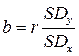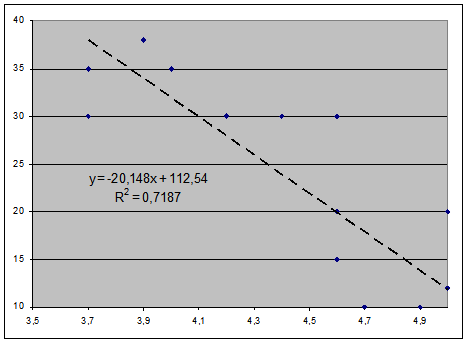
´Задача 2.2.18. Для задачи 2.1.4 построить график и определить уравнение регрессии.
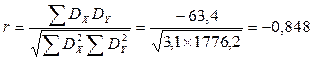r 2 = 0,719 как на графике.
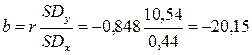, a = 23,5 – 4,4(–20,15) = 112,54.
Итак, уравнение регрессии
y = 112,54 – 20,15x .
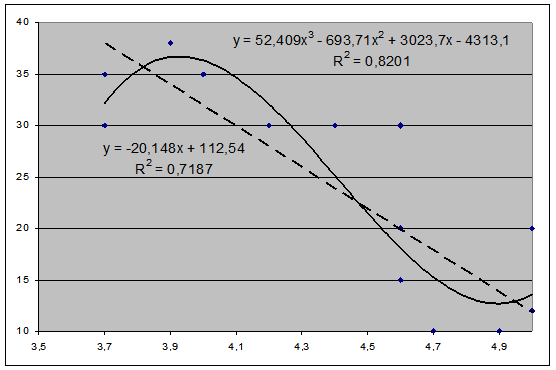
Но так ли это на самом деле? Оказывается, в данном примере была (умышленно) допущена неточность. Все уравнения, по которым проводились расчеты, применяются только в случае линейной зависимости. На графике же точки расположены явно не на одной линии, и мы можем предположить, что регрессия может быть иной, нелинейной. Если зависимость y от x нелинейная, то иногда эту зависимость можно линеаризовать с помощью преобразования переменных x и y. Линеаризацию можно провести с помощью формул табл. П 3.8. Но для данного случая остановимся на полигональной зависимости
y = b 0 x0 + b1 x1 + b2 x2 + b3 x3 + … + bn xn
| где n – степень функции. Используя электронную таблицу MS Excel, строим полигональную линию тренда (n = 3) и получаем r = – 0,906 ( r 2 = 0,820). Это выше, чем при расчетах линейной зависимости. Если вы не можете принять решение, какую формулу подобрать для конкретной регрессии, то выберете ту, при которой получается максимальный коэффициент корреляции. | 
|
Контрольные вопросы
1. Опишите схему классического экспериментального плана с большими объемами выборок n.
2. Перечислите и охарактеризуйте шкалы представления данных.