Задание студентам на самостоятельную работу.
С помощью MS Excel построить графики:
1. Полигон распределения частот (абсцисса – значение признака; ордината – число вариант);
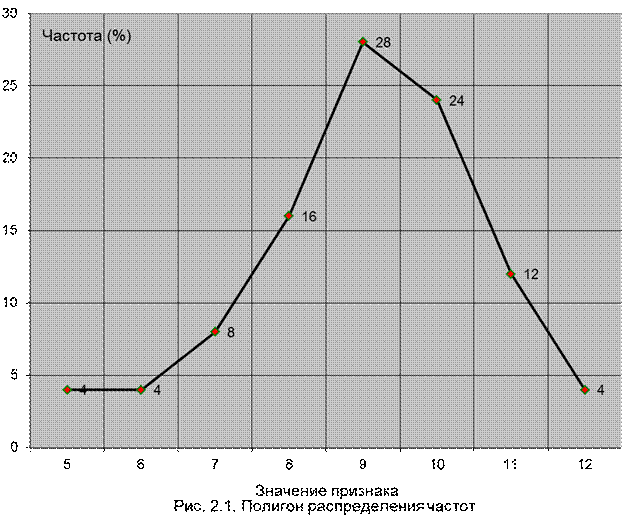
2. Гистограмму распределения удачных бросков (абсцисса – значение признака; ордината – число вариант);
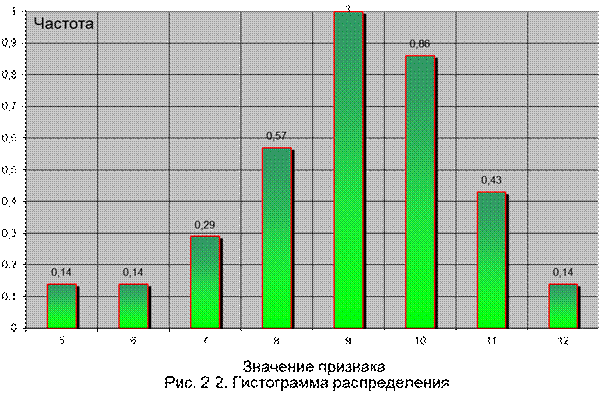
3. Кумуляту распределения (абсцисса – значение признака; ордината – кумулированные частоты).
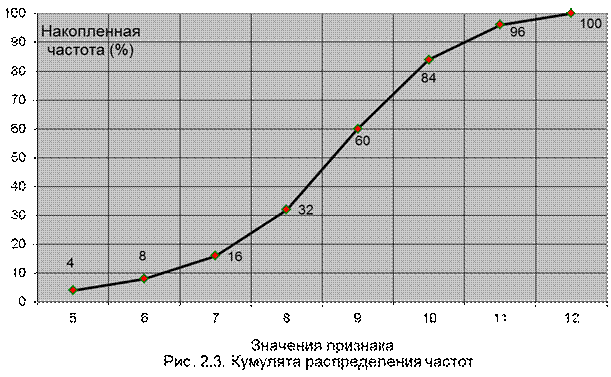
´Задача 2.3 [1]. Исследовалась динамика венозного давления ∆вд у 8 больных при эпидуриальной анестезии:
15, 20, 20, 25, 30, 30, 35, 55.
| Выявить аномальность числа «55» в выборке для P ≤ 0,05 Критериальная статистика вычисляется по формуле В нашем случае D 8 =(55-28,75)/11,66=2,25, что больше табличного D 8 =2,17 для P ≤0,05
Вывод: «55» – аномально. |
| X i | d | d2 |
| 1 | 15 | -13,75 | 189,06 | |
| 2 | 20 | -8,75 | 76,56 | |
| 3 | 20 | -8,75 | 76,56 | |
| 4 | 25 | -3,75 | 14,06 | |
| 5 | 30 | 1,25 | 1,56 | |
| 6 | 30 | 1,25 | 1,56 | |
| 7 | 35 | 6,25 | 39,06 | |
| 8 | 55 | 26,25 | 689,06 | |
| M=28,75 | SS=1087,50 | |||
|
|
| δ2 =135,94 | ||
|
|
| SD=11,66 | ||
|
|
| D=2,25 | ||
|
| P≤ 0,05 | Dtab=2,17 |
Критические значения статистики Dn
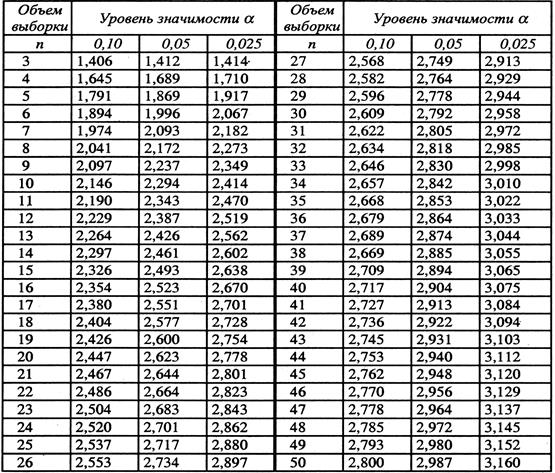
Примечание: Распределение величины Dn получено Карлом Пирсоном (1857 – 1936) и Николаем Васильевичем Смирновым (1910 – 1966). В таблице приведены значения, рассчитанные Н.В. Смирновым и Ф. Граббсом в 1950 г.
´Задача 2.4 [5]. Содержание Ca (мг%) в сыворотке крови клинически здоровых павианов гамадрилов.
| 13,6 | 12,9 | 12,3 | 9,9 | 12,7 | 11,7 | 10,8 | 10,4 | 10,9 | 10,2 |
| 14,7 | 10,4 | 11,6 | 11,7 | 12,1 | 10,9 | 12,1 | 9,2 | 10,7 | 11,5 |
| 13,1 | 10,9 | 12,0 | 11,1 | 13,5 | 11,2 | 13,5 | 10,1 | 14,0 | 10,0 |
| 11,6 | 12,4 | 11,9 | 11,4 | 12,8 | 11,4 | 10,9 | 12,7 | 13,8 | 13,2 |
| 11,9 | 10,8 | 11,0 | 12,6 | 10,0 | 10,3 | 12,7 | 11,7 | 12,1 | 13,8 |
| 12,2 | 11,9 | 11,6 | 10,6 | 11,1 | 10,7 | 12,3 | 11,5 | 11,2 | 11,5 |
| 12,7 | 10,5 | 11,2 | 11,9 | 9,7 | 13,0 | 9,6 | 12,5 | 11,6 | 9,0 |
| 11,5 | 12,3 | 12,6 | 12,6 | 12,8 | 12,5 | 12,8 | 11,4 | 12,5 | 12,3 |
| 14,5 | 12,3 | 12,8 | 11,7 | 12,2 | 12,3 | 11,6 | 12,0 | 13,5 | 12,5 |
| 11,6 | 11,9 | 12,0 | 11,4 | 14,7 | 11,3 | 13,2 | 14,3 | 13,2 | 14,2 |
Требуется: сгруппировать данные (n = 100) в вариационный ряд (упорядоченные по возрастанию элементы выборки).
1. Устанавливаем величину классового интервала по формуле для выборки объемом 100 и менее единиц
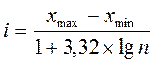 = 0,8
= 0,8
2. Строим таблицу.
| Классы по уровню Ca, мг% | 8,6-9,3 | 9,4-10,1 | 10,2-10,9 | 11,0-11,7 | 11,8-12,5 | 12,6-13,3 | 13,4-14,1 | 14,2-14,9 | |
| Срединные значения классов | 9,0 | 9,8 | 10,6 | 11,4 | 12 ,2 | 13,0 | 13,8 | 14,6 | |
| Частота | 2 | 6 | 15 | 23 | 25 | 17 | 7 | 5 | 100 |
| Накопленная частота | 2 | 8 | 23 | 46 | 71 | 88 | 95 | 100 |
3. С помощью MS Excel построим графики:
а) Гистограмму распределения Ca в крови (абсцисса – границы классовых интервалов; ордината – частоты вариант);
б) Кумуляту (абсцисса – значения классовых вариант; ордината – кумулированные частоты).
МЕРЫ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ
Величины, отражающие все результаты измерений в распределении, называются центральной тенденцией. Тремя характеристиками центральной тенденции являются: среднее, медиана и мода. Среднее (M) – это среднее арифметическое, которое нахоится путем сложения всех результатов (Σ xi ) и деления полученной суммы на количество результатов (n).
Медиана (Me) – это значение, расположенное в центре распределения и разделяющее все наблюдения на две половины. Мода (Mo) – это величина или категория, которая появляется наиболее часто. Среднее отклонение (более подробно см. ниже) вычисляют по следующей формуле:
|
´Задача 2. 5 . Каков средний возраст женщин, участвовавших в исследовании? Поскольку мы исключаем из этого анализа мужчин, то должны подсчитать только те результаты в графе возраст, которым соответствует числовое значение 2 в графе пол (номера в этом анализе не нужны; они приведены в качестве справки) | Номер | Возраст (xi) |
| X1 | X4 | |
| 3 | 17 | |
| 5 | 23 | |
| 7 | 18 | |
| 8 | 32 | |
| 9 | 22 | |
| 10 | 20 | |
| 12 | 18 | |
| 15 | 19 | |
| п = 9 | Σ xi = 206 |
ОЦЕНКА ИЗМЕНЧИВОСТИ
Стандартное отклонение ( standard deviation – SD ) – это один из наиболее часто используемых показателей того, насколько величины отличаются от среднего. Формула для вычисления стандартного отклонения:
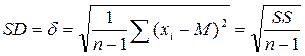 .
.
´Задача 2. 6 . Каково стандартное отклонение для количества часов, отработанных в неделю мужчинами?
· Выберите из графы отработанные часы данные по мужчинам (мужчинам в графе пол соответствует числовое значение 1).
· Подсчитайте для этой группы среднее арифметическое М.
· Вычислите отклонение D – отнимите среднее значение от количества часов, отработанных каждым человеком D =( xi – M ),
· Возведите в квадрат каждую из полученных величин D 2 =( xi – M )2.
· Вычислите сумму квадратов отклонений SS = Σ D 2.
· Подставьте эти величины в формулу SD.
| X1 | X7 | ||
| Номер | Отработанные часы (xi) | D | D2 |
| 1 | 38 | 12 | 144 |
| 2 | 15 | –11 | 121 |
| 4 | 30 | 4 | 16 |
| 6 | 35 | 9 | 81 |
| 11 | 20 | –6 | 36 |
| 13 | 30 | 4 | 16 |
| 14 | 30 | 4 | 16 |
| 16 | 10 | –16 | 256 |
| n = 8 | Σxi = 208 | SS = 686 |
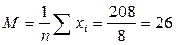
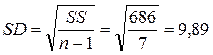
Помимо средней арифметической нередко требуется определить среднее гармоническое, квадратическое, кубическое, а так же их средневзвешенные значения. В приведенных ниже примерах ознакомимся с ними.
Вычисление средней арифметической
способом произведений или основным
| ´Задача 2.7 [5]. Длина тела личинок щелкуна (мм), отобранных случайным способом в посеве озимой ржи, варьировала следующим образом: 7, 10, 14, 12, 15, 16, 12. Используя MS Excel, определить: Формулы: =СРЗНАЧ(А1:А7) =СУММ(B1:B7) =B1^2 =КОРЕНЬ(C8/(7-1)) | Длина личинок, мм | D | D 2 | ||
| 7 | -5 | 28 | |||
| 10 | -2 | 5 | |||
| 14 | 2 | 3 | |||
| 12 | 0 | 0 | |||
| 15 | 3 | 7 | |||
| 16 | 4 | 14 | |||
| 12 | 0 | 0 | |||
| M = 12 | 0 | SS = 57 | |||
| 1) среднее арифметическое: |
| ||||
| 2) дисперсию – dispersion или variance: |
| ||||
| 3) стандартное отклонение (среднеквадратическую ошибку) – standard deviation |
| ||||
´Задача 2.8 [5]. На свиноферме зарегистрирован опорос 64 свиноматок. От каждой свиноматки получено следующее количество живых поросят: | 8 | 10 | 6 | 10 | 8 | 5 | 11 | 7 |
| 10 | 6 | 9 | 7 | 8 | 7 | 9 | 11 | |
| 8 | 9 | 10 | 8 | 7 | 8 | 8 | 11 | |
| 7 | 10 | 8 | 8 | 5 | 11 | 8 | 10 | |
| 12 | 7 | 5 | 7 | 9 | 7 | 5 | 10 | |
| 8 | 9 | 7 | 12 | 8 | 9 | 6 | 7 | |
| 8 | 7 | 11 | 8 | 6 | 7 | 9 | 10 | |
| 6 | 7 | 6 | 12 | 8 | 10 | 6 | 11 |
Используя MS Excel определить:
| 1) среднее арифметическое (взвешенное (Σ pi = n)): |
| ||||
| 2) дисперсию (при учете весов): |
| ||||
| 3) стандартное отклонение: |
| ||||
|
|
| ||||
| Классы (xi) | Частоты (pi) | xipi | xi2 | pixi2 | |
| 5 | 4 | 20 | 25 | 100 | |
| 6 | 7 | 42 | 36 | 252 | |
| 7 | 13 | 91 | 49 | 637 | |
| 8 | 15 | 120 | 64 | 960 | |
| 9 | 7 | 63 | 81 | 567 | |
| 10 | 9 | 90 | 100 | 900 | |
| 11 | 6 | 66 | 121 | 726 | |
| 12 | 3 | 36 | 144 | 432 | |
| n = Σ pi = 64 | Σ xipi =528 | Σ pi xi2= 4574 | |||
Вычисление средней гармонической
Средняя гармоническая простая: 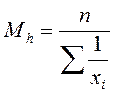
´Задача 2.9 [5]. 5 доярок в течение 1 часа ручным способом надоили следующее количество молока: 10, 20, 25, 30, 20 – всего 105 л. Сколько времени затрачивает в среднем доярка на выдаивание 1 л молока?
| М = 105/5 = 21 л . t= 60 / 21 = 2,86 мин. | М h =5 /(1/10 +1/20 +1/25 +1/30 +1/20) = 5 /0,273 = 18,31 л t = 60/18,31 = 3 , 23 мин. |
Средняя гармоническая взвешенная: 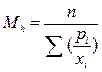 .
.
´Задача 2.10 [5].
| Плотность колосьев ржи = (кол-во зерен в колосе) / (длина колоса). Объем выборки – 20 растений | Длина колосьев | 8 | 9 | 10 | 11 | 12 |
| Кол-во зерен в колосе | 36 | 38 | 40 | 41 | 42 | |
| Частота (n = 20) | 2 | 5 | 10 | 2 | 1 | |
| Плотность колосьев | 4,5 | 4,2 | 4,0 | 3,7 | 3,5 |
Средняя плотность колосьев в выборке:
М h= 20 / (2×1/4,5 + 5×1/4,2 + 10×1/4,0 + 2×1/3,7 + 1×1/3,5) = 20 / 5 = 4.
Сравните: М = (2×4,5 + 5×4,2 + 10×4,0 + 2×3,7 + 1×3,5) / 20 = 81/20 = 4,1 .
Вычисление средней квадратической
Применяется при выражении признаков мерами площади
Средняя квадратическая простая 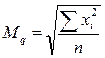 ; взвешенная
; взвешенная 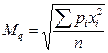 .
.
´Задача 2.11 [5].
| Измерялся – диаметр корзинок подсолнуха в см., n = 10 | Диаметр корзинок (xi) | 8 | 11 | 13 | 15 | 16 | 17 |
| Число случаев (pi) | 1 | 1 | 2 | 3 | 2 | 1 |
Средний размер признака
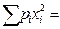 1×82+1×112 +2×132 +3×152 +2×162 +1×172 =1999.
1×82+1×112 +2×132 +3×152 +2×162 +1×172 =1999. 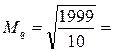 14,1 см.
14,1 см.
Сравните: М = (1×8 +1×11 +2×13 +3×15 +2×16 +1×17) / 10 = 139 /10 = 13,9 см.
Вычисление средней кубической
Применяется при выражении признаков мерами объема.
Средняя кубическая простая 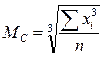 ; взвешенная
; взвешенная 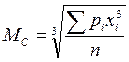 .
.
´Задача 2.12 [5]. Измерялся диаметр
| яиц в мм [полусумма большого и малого диаметров], n = 18 яиц | Диаметр яиц (xi) | 47 | 48 | 50 | 54 | 56 | 60 |
| Число случаев (pi) | 2 | 4 | 6 | 3 | 2 | 1 |
Средний размер признака
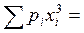 2×473 + 4×483 + 6×503 + 3×543 + 2×563 + 1×603 = 24397;
2×473 + 4×483 + 6×503 + 3×543 + 2×563 + 1×603 = 24397;
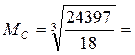 51 мм.
51 мм.
Вычисление средней геометрической
Применяется при увеличении линейных размеров тела, прироста численности популяции за определенный промежуток времени
Средняя геометрическая 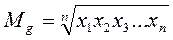
обычно вычисляется с помощью десятичных логарифмов по формуле
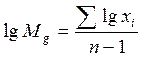 .
.
| ´Задача 2.13 [5]. Живая масса подопытных мышей изменяется с возрастом. Средняя геометрическая недельных абсолютных прибавок массы мышей за первые 9 недель их жизни lgМ g =7,58895/8 =0,94861,
М g = 8,9 г.
Сравните: М =77/9 = 9,6 г. | Возраст мышей (неделя) | Живая масса, г, xi | Абсолютные недельные прибавки массы, г | Логарифм прибавок массы |
| 1 | 10 | - | - | |
| 2 | 15 | 5 | 0,69897 | |
| 3 | 20 | 5 | 0,69897 | |
| 4 | 27 | 7 | 0,84510 | |
| 5 | 35 | 8 | 0,90309 | |
| 6 | 46 | 11 | 1,04139 | |
| 7 | 58 | 12 | 1,07918 | |
| 8 | 72 | 14 | 1,14613 | |
| 9 | 87 | 15 | 1,17609 | |
| Сумма | 77 | 7,58892 |
| Если признак варьируется непрерывно и выборка группируется в интервальный вариационный ряд, то
где Qi = x 2 / x 1 lgМ g = 0,93806 / 8 = 0,1173,
М g = 1,310 г.
Сравните: М i =10,50/8 =1,313 г. | Возраст мышей (неделя) | Живая масса, г, xi | Относительные недельные прибавки массы, г, Q | Логарифм прибавок массы lgQ |
| 1 | 10 | - | - | |
| 2 | 15 | 1,50 | 0,17609 | |
| 3 | 20 | 1,33 | 0,12385 | |
| 4 | 27 | 1,35 | 0,13033 | |
| 5 | 35 | 1,30 | 0,11394 | |
| 6 | 46 | 1,31 | 0,11727 | |
| 7 | 58 | 1,26 | 0,10037 | |
| 8 | 72 | 1,24 | 0,09342 | |
| 9 | 87 | 1,21 | 0,08279 | |
| Сумма | 10,50 | 0 ,93806 |
Используют также следующую формулу: 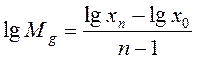 .
.
´Задача 2.14 [5]. Селекция гибридного хлопчатника за 5 лет позволила увеличить длину волокна с 26,3 мм до 31,0 мм. Определить среднегодовой эффект.
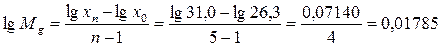 .
.
М g = 0,1044мм → 10,44% → Среднегодовой эффект: 10,44/5 = 2,1%.
Вычисление коэффициента вариации: 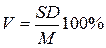 .
.
| ´Задача 2.15 [5]. На кролиководческой ферме взвешивание 35 животных показало следующий результат: | 3,0 | 2,7 | 2,1 | 1,6 | 1,2 | 1,6 | 2,2 |
| 2,1 | 2,3 | 1,5 | 1,1 | 2,2 | 2,5 | 2,4 | |
| 1,9 | 2,1 | 2,3 | 1,3 | 1,0 | 1,8 | 1,9 | |
| 1,8 | 3,2 | 2,1 | 2,9 | 3,0 | 1,3 | 1,9 | |
| 2,6 | 1,5 | 2,4 | 2,7 | 1,9 | 2,0 | 2,6 |
Сравнить V двух выборок – 35 кроликов и 64 поросят (см. задачу 2.8).
Vкроликов = 27,3%, Vпоросят = 22,5%.
Определение медианы
Медиана (Me) – средняя, относительно которой ряд распределения делится на 2 половины (в обе стороны от медианы) одинаковое количество вариант.
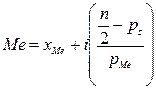 ,
,
где: XMe – нижняя граница интервала, в котором находится Ме или полусумма соседних классовых вариант; i – величина классового интервала; n – объем выборки; ps – число накопленных частот, стоящее перед медианным классом; pMe – частота медианного класса.
´Задача 2.16 [5]. (см. Задачу 2.4) Вычислить Ме ряда распределения Са (мг%) в сыворотке крови павианов гамадрилов
| Классы по содержанию Са в сыворотке крови | Срединные значения классов | Частоты (pi) | Накопленные частоты (ps) |
| 8,6 – 9,3 | 9,0 | 2 | 2 |
| 9,4 – 10,1 | 9,8 | 6 | 8 |
| 10,2 – 10,9 | 10,6 | 15 | 23 |
| 11,0 – 11,7 | 11,4 | 23 | 46 |
| 11,8 – 12,5 | 12,2 | 25 | 71 |
| 12,6 – 13,3 | 13,0 | 17 | |
| 13,4 – 14,1 | 13,8 | 7 | |
| 14,2 – 14,9 | 14,6 | 5 | |
| 100 |
Вариант 1. i = 0,8. Величина n /2= 50 находится между ps = 46 и ps = 71.
Границы интервала для (ps = 71) – 11,8 ÷ 12,5 т. е. pMe = 25.
По формуле: Ме = 11,8 + 0,8 (50 – 46) / 25 = 11,93 .
Вариант 2. По формуле: Ме = (11,4 + 12,2) / 2 + 0,8 (50 – 46)/25 = 11,93 .
´Задача 2.17 [5] (см. задачу 2.6). Вычислить Ме ряда распределения численности поросят.
| Классы (xi) | Частоты (pi) | Накопленные частоты | Величина n /2= 32 находится между ps = 24 и ps = 39.
То xMe = (7+8)/2 = 7,5; pMe = 15.
По формуле: Ме = 7,5 + 1 (32 – 24)/15 = 7,5 + 0,53 = 8,03. |
| 5 | 4 | 4 | |
| 6 | 7 | 11 | |
| 7 | 13 | 24 | |
| 8 | 15 | 39 | |
| 9 | 7 | ||
| 10 | 9 | ||
| 11 | 6 | ||
| 12 | 3 | ||
| Σ pi = 64 |
Определение моды
Мода (Mo) – наиболее часто встречающаяся, в данной выборке, величина. Класс с наибольшей частотой называется модальным.
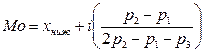 ,
,
где: X ниж – нижняя граница модального класса; i – величина классового интервала; p 1 – частота класса, предшествующего модальному; p 2 – частота модального класса; p 3 – частота класса, следующего за модальным.
| ´Задача 2.18 [5] (см. задачу 2.4). Вычислить (используя MS Excel) Мо ряда распределения Са (мг%) в сыворотке крови павианов гамадрилов.
i = 0,8. По формуле Мо = 11,8 +0,8 (25-23) / (2×25-23-17) = 11,8+0,16 = 11,96. | Классы по содержанию Са в сыворотке крови | Срединные значения классов | Частоты (pi) | Накопленные частоты (ps) |
| 8,6 – 9,3 | 9,0 | 2 | 2 | |
| 9,4 – 10,1 | 9,8 | 6 | 8 | |
| 10,2 – 10,9 | 10,6 | 15 | 23 | |
| 11,0 – 11,7 | 11,4 | 23 | 46 | |
| 11,8 – 12,5 | 12,2 | 25 | 71 | |
| 12,6 – 13,3 | 13,0 | 17 | ||
| 13,4 – 14,1 | 13,8 | 7 | ||
| 14,2 – 14,9 | 14,6 | 5 | ||
| 100 |
Хи -квадрат
Хи-квадрат (χ2) – это непараметрический статистический показатель, используемый для определения того, отличается ли наблюдаемая частота результатов от ожидаемой частоты. Поскольку для подсчета χ2 необходимы частоты, можно использовать как количественные, так и качественные переменные. Формула для χ2, где О соответствует наблюдаемой (эмпирической) частоте, а Е – ожидаемой (теоретической):
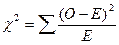 .
.
Степени свободы df для χ2, где R – число строк, а С – число столбцов в таблице распределения частот, находят с помощью формулы 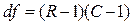 .
.
´Задача 2.19 [9]. Наблюдается ли различие между уровнем знаний женщин и мужчин? При вычислении χ2 желательно пользоваться таблицами распределения частот, помогающими упорядочить О и Е частоты. В таблице распределения эмпирических частот подсчитываются суммы по столбцам, по строкам и общая сумма n . Чтобы подсчитать значение для каждой клетки в таблице распределения теоретических частот, умножьте сумму всей строки на сумму столбца и разделите полученный результат на общую сумму n. Затем эти величины О и Е используются в формуле для вычисления критерия хи-квадрат
Таблица распределения эмпирических частот ( O)
| Пол | Низкий | Высокий | Итого |
| Женщины | 6 | 3 | 9 |
| Мужчины | 2 | 6 | 8 |
| Итого | 8 | 9 | п = 17 |
Таблица распределения теоретических частот ( E)
| Пол | Низкий | Высокий | Итого |
| Женщины | (9×8)/17 = 4,24 | (9×9)/17 = 4,76 | 9 |
| Мужчины | (8×8)/17 = 3,76 | (8×9)/17 = 4,24 | 8 |
| Итого | 8 | 9 | п = 17 |
| Х2 | Х9 | |||||
| категория | Уровень знаний | O | Е | (O – Е ) | (O – Е ) 2 | (O – Е ) 2 /Е |
| Женщины | Низкий | 6 | 4,24 | 1,76 | 3,11 | 0,74 |
| 2 | Высокий | 3 | 4,76 | – 1,76 | 3,11 | 0,65 |
| Мужчины | Низкий | 2 | 3,76 | – 1,76 | 3,11 | 0,83 |
| 1 | Высокий | 6 | 4,24 | 1,76 | 3,11 | 0,74 |
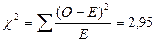 .
.
В нашем примере R = 2 и С = 2; таким образом, df = 1. Чтобы определить, превышает ли полученная нами величина χ2 (2,95) желаемое критическое значение, мы обращаемся к табл. П 3.З. Критическое значение при df = 1 и уровне значимости 0,05 равно 3,84. Полученная нами величина 2,94 меньше этого критического значения; следовательно, между мужчинами и женщинами отсутствует статистически значимое различие в уровне знаний.
Распределение случайно изменяющихся величин
Формула закона нормального распределения
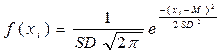 ,
,
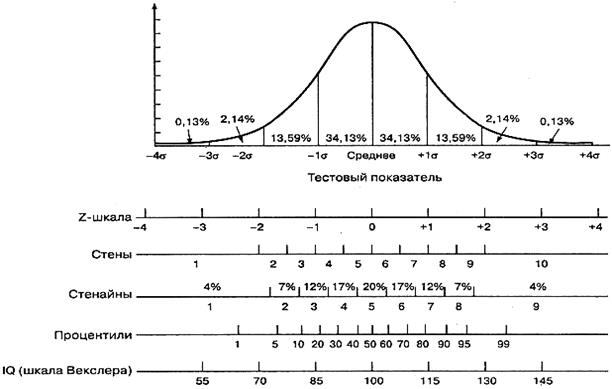 где: f ( xi ) – высота подъема кривой (плотность вероятности для значения xi); е – основание натурального логарифма (2,718); π – число «пи» (3,14159); М – среднее арифметическое; SD – стандартное отклонение.
где: f ( xi ) – высота подъема кривой (плотность вероятности для значения xi); е – основание натурального логарифма (2,718); π – число «пи» (3,14159); М – среднее арифметическое; SD – стандартное отклонение.









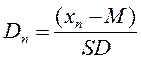
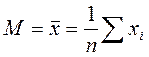
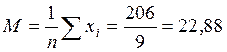 .
.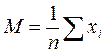 – простое = 12;
– простое = 12;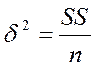 или (если n<30)
или (если n<30) 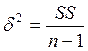 ;
;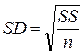 или (если n<30)
или (если n<30) 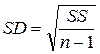 = 3,09.
= 3,09.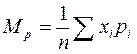 или
или 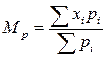 = 8,25;
= 8,25;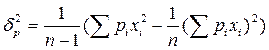 = 3,46;
= 3,46;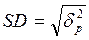 = 1 , 86 .
= 1 , 86 .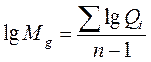 ,
,