Совокупность исходных данных
Как правило, совокупность исходных данных изображают в виде таблицы «объекты-признаки», в которой переменные (признаки) располагают в столбцах (графах), а данные индивидуального участника (объекты) – в строках (иногда называемых «записями»).
Совокупность исходных данных типа «объект-признак», приведенная в табл. 2.1, будет использоваться ниже для вычисления статистических показателей в примерах. Эта совокупность имитирует данные, которые могли бы быть получены в ходе небольшого исследования обучающихся экспериментального учебного курса. Цель исследования: определить факторы, влияющие на средний балл (СБ) успеваемости студентов в осеннем и весеннем семестрах.
Таблица 2.1
| Номер | Пол | Порядок рождения | Возраст | СБ осенний | СБ весенний | Отработанные часы | Удовлетворенность учебой | Уровень знаний |
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 |
| 1 | 1 | 3 | 60 | 3,9 | 3,9 | 38 | 1 | Н |
| 2 | 1 | 3 | 22 | 4,6 | 4,0 | 15 | 2 | В |
| 3 | 2 | 2 | 17 | 4,7 | 5,0 | 10 | 2 | В |
| 4 | 1 | 2 | 19 | 4,2 | 4,0 | 30 | 2 | В |
| 5 | 2 | 1 | 23 | 5,0 | 4,9 | 12 | 3 | В |
| 6 | 1 | 3 | 27 | 3,7 | 3,9 | 35 | 3 | В |
| 7 | 2 | 4 | 18 | 3,7 | 4,5 | 30 | 1 | Н |
| 8 | 2 | 2 | 32 | 4,4 | 4,9 | 30 | 2 | Н |
| 9 | 2 | 2 | 22 | 4,6 | 4,7 | 20 | 3 | Н |
| 10 | 2 | 1 | 20 | 4,9 | 5,0 | 10 | 1 | В |
| 11 | 1 | 2 | 29 | 5,0 | 5,0 | 20 | 3 | В |
| 12 | 2 | 2 | 18 | 4,0 | 4,0 | 35 | 3 | Н |
| 13 | 1 | 2 | 18 | 4,6 | 3,7 | 30 | 1 | В |
| 14 | 1 | 2 | 20 | 4,2 | 4,5 | 30 | 1 | Н |
| 15 | 2 | 3 | 19 | 4,0 | 4,1 | 35 | 2 | Н |
| 16 | 1 | 1 | 19 | 4,9 | 4,8 | 10 | 1 | В |
| 17 | 2 | 3 | 37 | 4,7 | 4,5 | 10 | 3 | Н |
Примечание: данные этой таблицы будут использоваться ниже в некоторых примерах.
Исходные данные включают для семнадцати объектов девять переменных (признаков): пять из них (X 1, X 2, X 3, X 8, X 9) – качественные, а четыре (X 4, X 5, X 6, X 7) – количественные. Как говорилось выше, шкала измерения обусловливает, какой статистический метод может быть применен для анализа имеющихся переменных; поэтому следует определить шкалу измерения для каждого признака-переменной, используемой в данном исследовании.
Х1 – номер испытуемого относится к номинальным данным; каждый номер – это «имя», за которым стоит конкретный человек (объект). Номер используется для идентификации записей (строк), и его никогда не следует использовать в каком бы то ни было виде анализа, кроме подсчета количества записей (n).
Х2 – переменная пол также номинальная; обе категории пола являются взаимоисключающими, поскольку участник исследования может принадлежать только одной из них. Для переменной «пол» номера являются символами категорий: 1 – мужчина, а 2 – женщина.
Х3 – порядок рождения представляет собой порядковую шкалу: 1 соответствует первенцу, 2 – родившемуся вторым и т. д.
Х4 – возраст относится к интервальным данным.
X 5 и X 6 – СБ , определенный по 5-балльной шкале – порядковые данные. СБ соответствуют две переменные: осень и весна.
Х7 – отработанные часы указаны за неделю – это относительная шкала.
Х8 – удовлетворенность учебой – это номинальная шкала, где 1 – высокая, а 3 – низкая удовлетворенность.
Х9 – уровень знаний (Н – низкий, В – высокий) – номинальная шкала.
´Задача 2.1. Из 120 студентов вуза, занимающихся физической культурой, требуется отобрать 25 человек для сдачи теста. Определить, какие из 120 студентов будут включены в состав исследуемой выборки?
Решение. 1. Каждому из 120 испытуемых присваивается номер от 1 до 120.
2. В таблице случайных чисел (по трем первым цифрам всех чисел) найти 25 чисел, не превышающих 120.
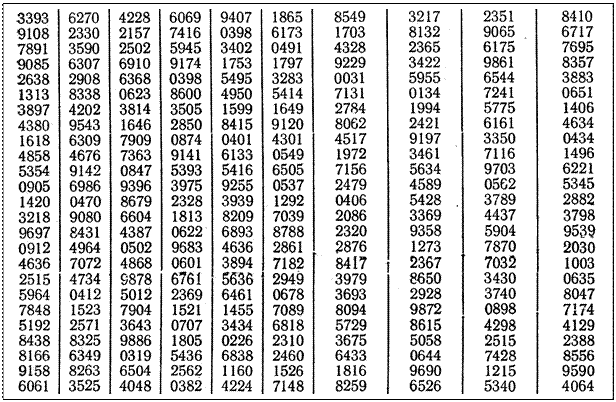
Таблица случайных чисел
Ответ. Тестирование должны пройти испытуемые под номерами:
90, 91, 47, 41, 62, 84, 50, 31, 39, 87, 60, 70, 38, 40, 22, 116, 49, 54, 53, 67, 3, 13, 64, 56, 89.
´Задача 2.2. Каждый из выбранных студентов выполнил тест на точность. Измерялось количество попаданий баскетбольного мяча в корзину из 20 попыток. Проанализировать выборку количества попаданий баскетбольного мяча в корзину из 20 попыток у 25 испытуемых:
6, 9, 5, 10, 7, 9, 8, 10, 9, 10, 8, 11, 9, 12, 9,10, 8, 10, 11, 9, 10, 9, 8, 7, 11.
| Значение признака | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Число вариант | 1 | 1 | 2 | 4 | 7 | 6 | 3 | 1 |
| Частота к 100% | 4 | 4 | 8 | 16 | 28 | 24 | 12 | 4 |
| Частота к 1 | 0,14 | 0,14 | 0,29 | 0,57 | 1,00 | 0,86 | 0,43 | 0,14 |
| Накопленная частота | 4 | 8 | 16 | 32 | 60 | 84 | 96 | 100 |








