2. Звонит звонок, затем собаке дают мясо; это повторяют несколько раз.
3. Звонит звонок (условный раздражитель), у собаки выделяется слюна; условный рефлекс образовался.
4. Если условный раздражитель повторяется несколько раз, но собаке не дают мяса, она перестает реагировать на звонок; рефлекс угасает.
Алгоритм выработки условного рефлекса – это алгоритм высшего порядка, который изменяет, в соответствии с внешними условиями, алгоритм работы управляющей системы (системы безусловных и закрепившихся условных рефлексов). Выявление алгоритмов работы сложной управляющей системы, каковой является головной мозг, очень важно для понимания работы мозга.
Еще в 1958 г. отечественный исследователь А.А. Ляпунов указывал: «Критерием того, что функционирование некоторой управляющей системы изучено, является возможность моделировать ее...». Зная алгоритм выработки условного рефлекса, можно моделировать это явление на ПК или построить нервную сеть, поведение которой будет описываться этим алгоритмом. Последнее значительно интереснее, так как построенная нервная сеть позволит представить себе структуру и принципы строения нервных сетей, делающих возможным обучение и приспособление к окружающей обстановке, адаптацию.
Обозначим безусловный раздражитель буквой F, событие «появился безусловный раздражитель» – p(F); p(F) = 1, если безусловный раздражитель появился и p(F)=0, если он не появился. Условный раздражитель обозначим G, и р(G) – событие «появился условный раздражитель».
Имеется специальный математический аппарат для описания строения алгоритмов – логические схемы алгоритмов. Отдельные части алгоритма, перерабатывающего информацию, называются операторами. Будем обозначать их прописными латинскими буквами. В алгоритм могут входить некоторые логические условия, которыми определяется дальнейший порядок выполнения алгоритма. Будем обозначать логическое условие Р(Е). Так, в нашем алгоритме логическими условиями будут Р(G) и P(F). Логическое условие, например Р(G) будет выполнено, если появляется раздражитель G.
Алгоритм состоит из нескольких частей – операторов. Последовательное выполнение нескольких операторов будем обозначать как их произведение. Например, запись
A1·A2·A3·A4
означает, что сначала выполняется оператор A1 , затем A2 и т. д.
Выражение, составленное из операторов и логических условий, называется логической схемой алгоритма.
Например, логическая схема алгоритма безусловного рефлекса (F→a):
1,2↓ K(F) P(F) 1↑Aω 2↑
где: К(F) – оператор ввода информации;
А – оператор выполнения действия а, т. е. этот оператор заставляет систему совершить действие а;
ω – тождественно ложное условие, т. е. оно всегда не выполняется и поэтому всегда означает переход по стрелке;
Стрелки в этой схеме означают переход к следующей oneрации в случае невыполнения логического условия. Каждая стрелка имеет начало (стрелка вверх) и конец (стрелка вниз). Начало и конец отмечаются одинаковыми цифрами.
Для приведенного алгоритма, если Р(F)= 1, т. е. появился безусловный раздражитель, алгоритм выглядит так:
2↓ K(F) Aω 2↑
т. е. при появлении F система отвечает действием а и возвращается в исходное состояние по стрелке 2 (так как ω – тождественно ложное условие, т. е. оно всегда не выполняется и поэтому обозначает безусловный переход по стрелке).
Построим теперь логическую схему алгоритма выработки простого условного рефлекса. Пусть в системе имеется запоминающий элемент, который хранит возбуждение, связанное с событием GΛF (Λ – логический оператор «И»). Этот накопитель имеет порог h и, когда хранимое в нем возбуждение превзойдет порог h, образуется связь между условным раздражителем и действием (G→a). Обозначим текущее значение содержимого накопителя r и введем логическое условие р(r≥h) такое, что:
р (r ≥ h) = 1, если r ≥ h;
р (r ≥ h) = 0, если r < h.
Накопление возбуждения может происходить по различным законам (см. ниже).
Введем операторы: R – оператор накопления возбуждения в накопителе по определенному закону; S – оператор нейтрализации части возбуждения в накопителе; K(F,G) – оператор ввода информации.
Логическая схема алгоритма запишется в виде:
3,4,7↓ K(F,G) p(G) 1↑ p(F) 2↑ R 5,6↓ Aω 3↑ 2↓ S p(r≥h) 4↑ ω 5↑ 1↓ p(¯F) 6↑ ω 7↑
Такая запись алгоритма позволяет уже в некоторой степени представить, какова должна быть структура нервной сети. В этой нервной сети должны быть представлены события G, F, GΛF; эта нервная сеть должна иметь запоминающий элемент (накопитель) и какие-то переключающие элементы, управляемые накопителем. Все эти элементы должны быть соединены в соответствии с алгоритмом.
Задача построения нервной сети по заданному алгоритму имеет неоднозначное решение, можно построить различные сети, реализующие данный алгоритм в зависимости от того, какой элемент взять за основу нервной сети. В связи с этим возникает задача построения модели нейрона, более точно соответствующей реальному нейрону, что требует уточнения нейрофизиологических данных о нем.
Однако несмотря на неоднозначность решения, принципы построения нервной сети, реализующей данный алгоритм, и ее структура в общих чертах останутся одинаковыми для всех возможных сетей, поведение которых описывается данным алгоритмом.
Рассмотрим теперь нервную сеть, реализующую описанный алгоритм (алгоритм выработки классического условного рефлекса). На рис. 1.1 приведена схема нервной сети, предложенная Дж. Нейманом еще в 1956 г.
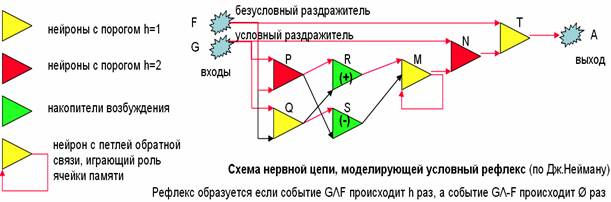
G – вход от условного раздражителя;
|
F – вход от безусловного раздражителя;
А – выход;
Р, N – нейроны с порогом h = 2;
Q, М, T – нейроны с порогом h = 1;
R, S – накопители возбуждения
Сеть имеет два входа (G, F) и один выход (А). В необученном состоянии раздражитель G не вызывает никакой реакции (А = 0); возбуждение же рецептора F вызывает реакцию А, что иллюстрирует наличие безусловного рефлекса.
Чтобы выработать условный рефлекс, необходимо некоторое время подавать совместно раздражители G и F.
При этом в результате каждого возбуждения пары входов G и F возбуждается нейрон Р, нейрон Q не возбуждается. Импульсы при совпадении G и F накапливаются в счетчике R, выход которого возбуждается только тогда, когда число пришедших импульсов превзойдет некоторую фиксированную величину. С выхода R возбуждение передается на нейрон М (h = l) с петлей обратной связи. Этот нейрон играет роль ячейки памяти. Теперь, если появляется один раздражитель G, возникает реакция А, так как нейрон N (порог h = 2) имеет один возбужденный вход (концевая пластина нейрона М). Условный рефлекс выработан. Если теперь на схему подается только сигнал G, то будет возбуждаться нейрон Q. Возбуждение нейрона Q передается на счетчик S и, если событие GΛ¯F повторяется несколько раз подряд, возбудится аксон счетчика, имеющий концевую тормозящую пластину на нейроне М, нейрон М тормозится – рефлекс угасает.
Если в процессе обучения наряду с событием GΛF происходит событие GΛ¯F, то возбуждается нейрон Q и происходит сброс счетчика R. Обучение нужно начинать сначала. Аналогичная ситуация наблюдается при гашении рефлекса.
Рассмотрим, какие законы накопления и нейтрализации возбуждения реализуют операторы R и S. Из рассмотрения схемы нервной сети видно, что оператор R реализует следующую функцию:
r1 = r + 1,
где r – содержимое накопителя. Порог накопителя h – фиксированная величина.
Оператор S более сложен; его можно представить в таком виде:
...р (r < h) 1↑ 2↓ ¯R ω 3↑ 1↓ S1 p(s > h1) 2↑ 3↓…
Здесь оператор ¯R означает нейтрализацию всего содержимого в накопителе R, т. е. ¯R(r)=0; оператор S1 реализуется функцией:
s1 = s + 1,
где: s – содержимое счетчика «забывания»; h1 – порог счетчика забывания.








