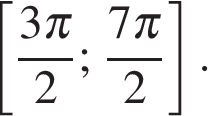При выполнении заданий 19-22 запишите ход решения и полученный ответ.
19. (3 балла) Найдите экстремумы функции у = -2 х3 -3х2 +12х -4 отрезке.[-15;8].
20. (3 балла) Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен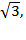 
а высота равна 2.
21. (3 балла) а) Решите уравнение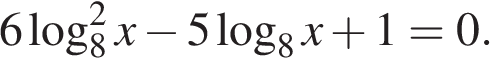 
б) Найдите все корни этого уравнения, принадлежащие отрезку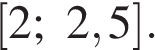 
22. (3 балла)
а) Решите уравнение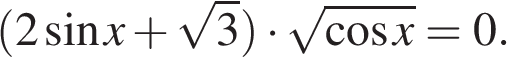 
б) Найдите все корни этого уравнения, принадлежащие отрезку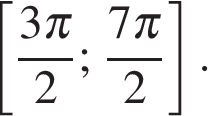 
Предэкзаменационная работа(1)
по математике 2022 год
Вариант №1
Критерии оценки выполнения работы
| Оценка | Число баллов необходимое для получения оценки |
| «3»(удовлетворительно) | 9-14 |
| «4»(хорошо) | 15-20 (не менее одного задания из дополнительной части) |
| «5»( отлично) | 21-30 (не менее двух заданий из дополнительной части) |
Обязательная часть
При выполнении заданий 1-8 запишите ход решения и полученный ответ
1. (1 балл) ) По тарифному плану «Просто как день» компания сотовой связи каждый вечер снимает со счёта абонента 16 руб. Если на счету осталось меньше 16 руб., то на следующее утро номер блокируют до пополнения счёта. Сегодня утром у Лизы на счету было 300 руб. Сколько дней (включая сегодняшний) она сможет пользоваться телефоном, не пополняя счёт?
2. (1 балл) В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на 25%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?
3.(1 балл) ) Решите уравнение.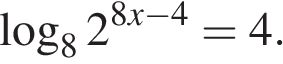 
.
4.(1 балл) Найдите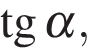 
если 
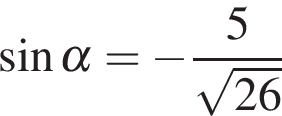и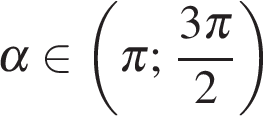 
5.(1 баллИз множества натуральных чисел от 10 до 19 наудачу выбирают одно число. Какова вероятность того, что оно делится на 3?
6.(1 балл) Найдите корень уравнения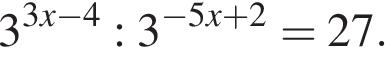 
7. (1 балл) Решите уравнение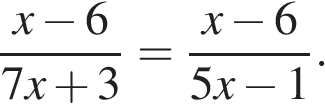 
Если уравнение имеет более одного корня, в ответе запишите больший из корней.
8. (1 балл)Решить неравенство: log 
(2-5x)< - 1
9. (1 балл)
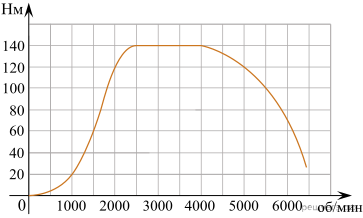На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н · м. Скорость автомобиля (в км/ч) приближенно выражается формулой v = 0,036n, где n — число оборотов двигателя в минуту. С какой наименьшей скоростью должен двигаться автомобиль, чтобы крутящий момент был не меньше 120 Н · м? Ответ дайте в километрах в час.
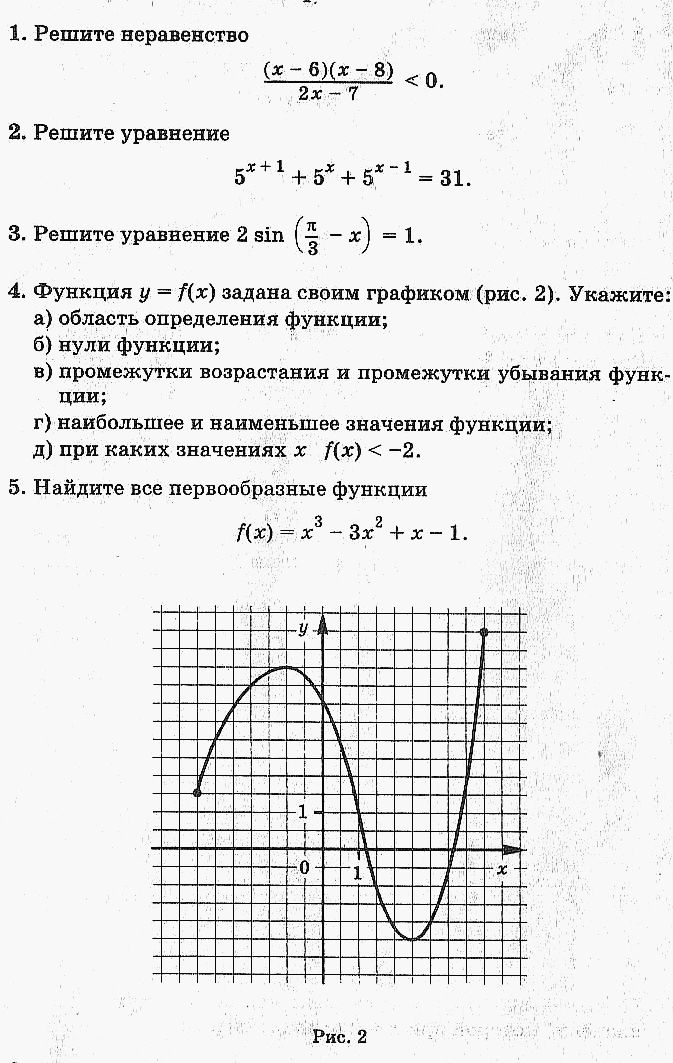
Используя график функции у = f ( x ) ( см. рис. ниже) ,
определите и запишите ответ.
10. (1 балл) Область определения функции.
11.(1 балл) Нули функции.
12. (1 балл) Промежутки возрастания и убывания функции.
При выполнении заданий 13-18 запишите ход решения и полученный ответ.
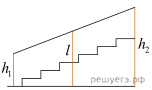13. (1 балл) Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил относительно земли равна 1,5 м, а наибольшая h2 равна 2,5 м. Ответ дайте в метрах.
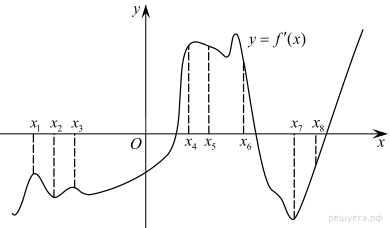14. (1 балл)
На рисунке изображён график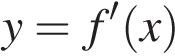 
- производной функции f(x).На оси абсцисс отмечены восемь точек: x1, x2, x3, ..., x8. Сколько из этих точек лежит на промежутках убывания функции f(x) ?
15. (1 балл) Решить неравенство :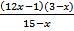 
>0
16. (1 балл) Найдите корень уравнения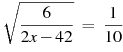 
17. (1 балл) Решите уравнение : sin2 x -6 sin x = 0
18. (1 балл) Даны два цилиндра. Радиус основания и высота первого равны соответственно 2 и 6, а второго — 6 и 7. Во сколько раз объём второго цилиндра больше объёма первого?
Дополнительная часть
При выполнении заданий 19-22 запишите ход решения и полученный ответ.
19. (3 балла) Найдите наименьшее значение функции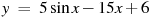 
на отрезке 
.
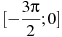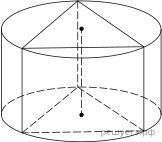20. (3 балла) Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 
а высота равна 2.
.21. (3 балла) а) Решите уравнение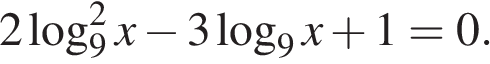 
б) Укажите корни этого уравнения, принадлежащие отрезку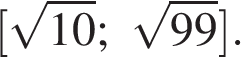 
22. (3 балла)
а) Решите уравнение (2 cosx -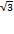 
) 
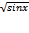=0
б) Найдите все корни этого уравнения, принадлежащие отрезку