Звіт про виконання лабораторної роботи № 4
Міністерство освіти та науки України
Черкаський національний університет ім. Б. Хмельницького
Факультет обчислювальної техніки, інтелектуальних та управляючих систем
Звіт про виконання лабораторної роботи № 4
з дисципліни
“ ВСТУП ДО КОМП’ЮТЕРНИХ НАУК ”
Перевірив роботу: Виконав роботу:
Студент групи КМ-13
_____________________ Вовна Р.В.
Черкаси, 2013
Лабораторна робота № 4
ПРОГРАМНЕ МОДЕЛЮВАННЯ МАШИННИХ АЛГОРИТМІВ ДІЛЕННЯ ЧИСЕЛ З ФІКСОВАНОЮ КРАПКОЮ
Мета роботи: Розглянути машинні алгоритми виконання операції ділення над числами у форматі з фіксованою крапкою
Теоретичні відомості: Машинне ділення організовано за тією ж схемою, як й звичайне десяткове ділення.
Алгоритм полягає в тому, що дільник спочатку зсувається вліво до старшого розряду діленого, а далі на кожнім кроці з діленого віднімається дільник, помножений на цифру частки. При цьому цифра частки підбирається так, щоб при вирахуванні вийшло найменше ненегативне число. Далі залишок від вирахування приймається за ділене. У випадку двійкової системи числення чергова цифра частки виходить з порівняння діленого і дільника. Порівняння це виробляється шляхом вирахування дільника з діленого. Якщо дільник менше (різниця менше нуля), то цифра частки приймається рівної 1, інакше - 0. В другому випадку ділене після порівняння необхідно відновити, додавши до нього регістр дільника. Далі дільник зсувається вправо на 1 розряд і операція продовжується ще n раз. Усього ж операція порівняння проводиться (n+1) раз.
Машинний алгоритм цього методу ділення в застосуванні до двійкових чисел представлений нижче:
Ділення з відновленням залишку. Вихідні дані: ділене в регістрі діленого, дільник у регістрі дільника і нуль у регістрі частки.
1. Зрушуємо дільник уліво доти, поки він не стане більше діленого (або поки не збіжаться їхні старші цифри), позначимо число таких зрушень n;
2. Порівнюємо дільник і ділене. Операція порівняння проводиться за допомогою вирахування, результат заноситься в регістр діленого. Якщо при вирахуванні дільника з діленого отримали заєм (тобто ділене менше дільника), то всуваємо в регістр частки праворуч цифру нуль. Інакше заносимо одиницю і йдемо до пункту 4;
3. Відновлюємо негативний залишок у регістрі діленого до стану перед порівнянням у пункті (2). Для цього додаємо значення дільника до регістра діленого (на кроці (2) при порівнянні ми віднімали);
4. Зрушуємо дільник вправо на один розряд. Якщо не виконана (n+1) ітерація, то перейти до пункту 2.
Розглянемо приклад:
Приклад ділення з відновленням залишку
Поділимо двійкове число 110102 на двійкове число 1012
| Крок | Регістр ділимого | Регістр дільника | Регістр частки |
| 011010 | 000101 | 000000 | |
| Зсув дільника до співпадання старших цифр | 011010 | 010100 | 000000 |
| Порівняння | 000110 | 010100 | 000001 |
| Зсув дільника | 000110 | 001010 | 000001 |
| Порівняння | 111100 | 001010 | 000010 |
| Відновлення залишку | 000110 | 001010 | 000010 |
| Зсув дільника | 000110 | 000101 | 000010 |
| Порівняння | 000001 | 001010 | 000101 |
Частка дорівнює 101, залишок 1.
У такий спосіб у регістрі частки сформується значення частки, а в регістрі діленого - значення залишку. Такий алгоритм ділення називається діленням з відновленням залишку і зрушенням дільника вправо. Існують і інші схеми ділення чисел з фіксованою крапкою.
Спробуємо оптимізувати алгоритм. Нехай Ai - залишок на i-тім кроці (після i-того порівняння), B - вихідний дільник. Розглянемо випадок відновлення залишку:
Ai+1 = Ai + B*2n-i - B*2n-i-1
де додавання відповідає відновленню залишку, вирахування - i+1-му порівнянню. Очевидно, що відновлення робити необов'язково:
Ai+1 = Ai + B*2n-i-1
Просто досить на наступному кроці замість операції вирахування при порівнянні застосувати додавання. Цей алгоритм одержав назву алгоритму ділення без відновлення залишків.
Розглянемо приклад:
Приклад ділення без відновлення залишку
Поділимо двійкове число 110102 на двійкове число 1012
| Крок | Регістр ділимого | Регістр дільника | Регістр частки |
| 011010 | 000101 | 0000000 | |
| Зсув дільника до співпадання старших цифр | 011010 | 010100 | 0000000 |
| Порівняння | 000110 | 010100 | 000001 |
| Зсув дільника | 000110 | 001010 | 000001 |
| Порівняння | 111100 | 001010 | 000010 |
| Зсув дільника | 111100 | 000101 | 000010 |
| Порівняння шляхом додавання | 000001 | 001010 | 000101 |
Частка дорівнює 101, залишок 1.
У випадку представлення операндів операції ділення у прямому коді знакові і числові розряди обробляються окремо, при цьому знак частки визначається шляхом додавання по модулю 2 знакових розрядів ділимого і дільника.
При виконанні ділення над операндами представленими у додатковому коді можливі наступні випадки комбінацій знаків дільника та ділимого:
1. X>0, Y>0, Z=X/Y>0 (X – ділене, Y – дільник, Z – частка). В даному випадку виконання операції ділення нічим не відрізняється від ділення додаткових чисел в прямому коді.
2. X<0, Y>0, Z=X/Y<0. Для отримання додаткового коду результату необхідно додати одиницю в n+1 розряд.
3. X>0, Y<0, Z=X/Y<0. Для отримання додаткового коду результату необхідно додати одиницю в n+1 розряд.
4. X<0, Y<0, Z=X/Y>0. На першому кроці алгоритму необхідно для формування вірного знаку частки необхідно із від’ємного діленого віднімати додатній дільник. Далі цей випадок зводиться до випадку №3. Всі цифри частки рівні знакам залишків.
Хід роботи
Варіант: Ділення з відновленням залишку. 8-ми розрядна сітка діленого, дільника. 16-ти розрядна сітка частки та залишку.
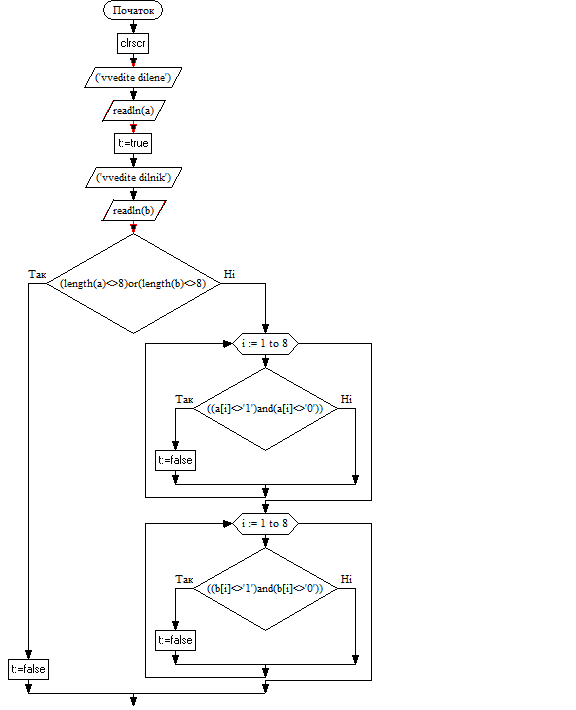
Блок-схема:
| 1 |
| 1 |
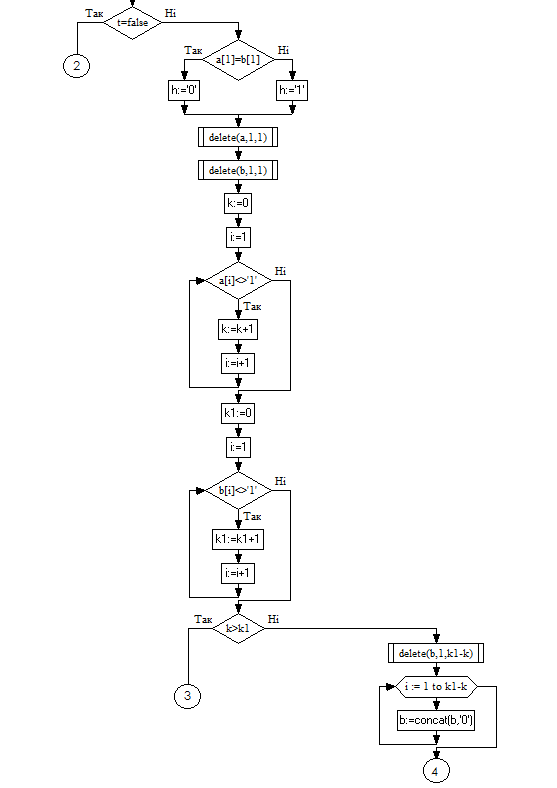
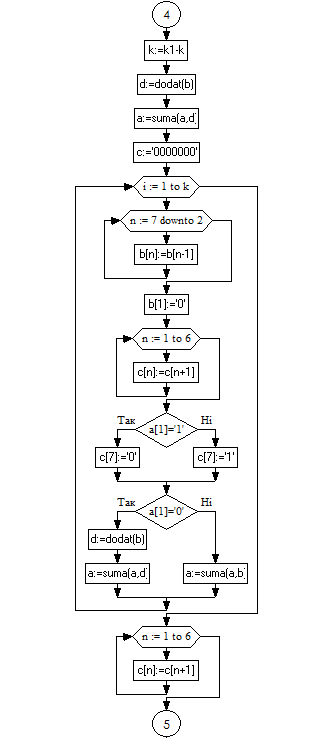
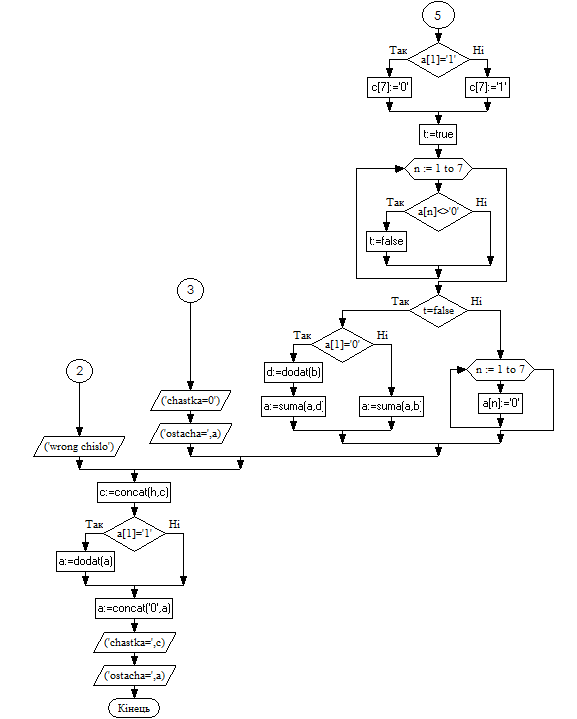
Проаналізувавши текст програми я дійшов висновку, що програма призначена для виконання ділення з відновленням залишку. Сітка діленого, дільника - 8-ми розрядна. 16-ти розрядна сітка частки та залишку.
Текст програми:
program Project1;
{$APPTYPE CONSOLE}
uses
SysUtils;
var a,b,d,c,h:string; k1,k,i,n:integer; t:boolean;
function suma(f,d:string):string;
var c,l:integer;
begin
l:=0;
suma:='0000000';
for c:=7 downto 1 do
if ((f[c]='1') and (d[c]='1') and (l=0)) or
((f[c]='1') and (d[c]='0') and (l=1)) or
((f[c]='0') and (d[c]='1') and (l=1)) then begin
suma[c]:='0';
l:=1;
end
else if ((f[c]='1') and (d[c]='0') and (l=0)) or
((f[c]='0') and (d[c]='1') and (l=0)) or
((f[c]='0') and (d[c]='0') and (l=1)) then begin
suma[c]:='1';
l:=0;
end
else if ((f[c]='1') and (d[c]='1') and (l=1)) then begin
suma[c]:='1';
l:=1;
end
else begin
suma[c]:='0';
l:=0;
end;
end;
function dodat(e:string):string;
var i:integer;
| 1 |
| 1 |
begin
i:=length(e);
while e[i]<>'1' do i:=i-1;
for i:=(i-1) downto 1 do
if e[i]='1' then e[i]:='0'
else e[i]:='1';
dodat:=e;
end;
begin
writeln('vvedite dilene'); readln(a); t:=true;
writeln('vvedite dilnik'); readln(b);
if (length(a)<>8) or (length(b)<>8) then t:=false
else begin
for i:=1 to 8 do
if ((a[i]<>'1') and (a[i]<>'0')) then t:=false;
for i:=1 to 8 do
if ((b[i]<>'1') and (b[i]<>'0')) then t:=false;
end;
if t=false then writeln('wrong chislo')
else begin
if a[1]=b[1] then h:='0'
else h:='1';
delete(a,1,1);
delete(b,1,1);
k:=0;
i:=1;
while a[i]<>'1' do begin
k:=k+1;
i:=i+1;
end;
k1:=0;
i:=1;
| 2 |
| 2 |
while b[i]<>'1' do begin
k1:=k1+1;
i:=i+1;
end;
if k>k1 then begin
writeln('chastka=0');
writeln('ostacha=',a);
end
else begin
delete(b,1,k1-k);
for i:=1 to k1-k do b:=concat(b,'0');
k:=k1-k;
d:=dodat(b);
a:=suma(a,d);
c:='0000000';
for i:=1 to k do begin
for n:=7 downto 2 do b[n]:=b[n-1];
b[1]:='0';
for n:=1 to 6 do c[n]:=c[n+1];
if a[1]='1' then c[7]:='0'
else c[7]:='1';
if a[1]='0'then begin
d:=dodat(b);
a:=suma(a,d);
end
else a:=suma(a,b);
end;
for n:=1 to 6 do c[n]:=c[n+1];
if a[1]='1' then c[7]:='0'
else c[7]:='1';
| 3 |
| 3 |
t:=true;
for n:=1 to 7 do if a[n]<>'0' then t:=false;
if t=false then if a[1]='0' then begin
d:=dodat(b);
a:=suma(a,d);
end
else a:=suma(a,b)
else for n:=1 to 7 do a[n]:='0';
end;
end;
c:=concat(h,c);
if a[1]='1' then a:=dodat(a);
a:=concat('0',a);
writeln('chastka=',c);
writeln('ostacha=',a);
Readln;
end.
Робота програми:

Висновок: Виконуючи лабораторну роботу я ознайомився з програмним моделюванням машинного алгоритму ділення чисел з фіксованою крапкою. Також я розглянув машинні алгоритми виконання операції ділення над числами у форматі з фіксованою крапкою.








