VIII класс: Тема 4. Подобие треугольников.

Дата: 2025-05-21; Просмотры: 5

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

1. Определение и свойства подобных треугольников.

Напомним, что числа a ₁ , a ₂ , a ₃ , …, a_n называются пропорциональными числам b ₁ , b ₂ , b ₃ , …, b_n, если выполняется равенство: 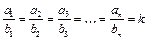, где k – число, называемое коэффициентом пропорциональности. Например, числа 6, ‑7,5 и 15 пропорциональны числам ‑4, 5 и ‑10 с коэффициентом пропорциональности ‑1,5, поскольку .

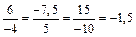Замечание: О пропорциональности чисел имеет смысл говорить, если они связаны пропорцией. А так как пропорцию можно составить не менее чем из четырех чисел, понятие пропорциональности применимо как минимум к четырем числам (одна пара чисел пропорциональна другой паре, или одна тройка пропорциональна другой, и т.д.).

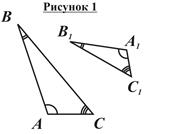
Прежде чем дать определение подобных треугольников, рассмотрим два треугольника с попарно равными углами (на рисунке 1 ÐA = ÐA₁, ÐB = ÐB₁, ÐC = ÐC₁). Стороны, противолежащие соответственно равным углам треугольников с попарно равными углами, называются сходственными. Так, на рисунке 1 стороны AB и A₁B₁, AC и A₁C₁, BC и B₁C₁, ‑ сходственные, поскольку лежат напротив соответственно равных углов треугольников ABC и A₁B₁C₁.

Дадим теперь определение подобных треугольников:

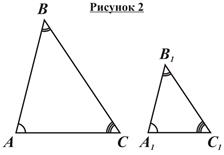Два треугольника называются подобными, если их углы попарно равны, а сходственные стороны пропорциональны. При этом отношение сходственных сторон подобных треугольников называется коэффициентом подобия. Обозначаются подобные треугольники следующим образом: ΔABC ~ ΔA₁B₁C₁. Итак, на рисунке 2 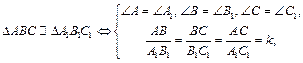где k – коэффициент подобия. Из рисунка 2 видно, что у подобных треугольников одинаковые пропорции, и отличаются они лишь масштабом.

Замечание 1: Равные треугольники подобны с коэффициентом 1.

Замечание 2: При обозначении подобных треугольников следует упорядочить их вершины таким образом, чтобы углы при них были попарно равны. Например, применительно к изображенным на рисунке 2 треугольникам некорректно говорить, что ΔABC ~ ΔB₁C₁A₁. Соблюдая правильный порядок вершин, удобно выписывать пропорцию, связывающую сходственные стороны треугольников, не обращаясь к чертежу: в числителе и знаменателе соответствующих отношений должны стоять пары вершин, занимающих одинаковые позиции в обозначении подобных треугольников. К примеру, из записи «ΔABC ~ ΔKNL» следует, что ÐA = ÐK, ÐB = ÐN, ÐC = ÐL, и .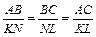

Замечание 3: Требования, предъявленные определением к подобным треугольникам, являются избыточными. Ниже будут доказаны признаки подобия треугольников, предъявляющие меньше требований к подобным треугольникам.

Сформулируем свойства подобных треугольников:

1. Отношение соответственных линейных элементов подобных треугольников равно коэффициенту их подобия (линейными называются величины, измеряемые в единицах длины; к примеру, сторона, периметр, медиана – линейный элемент, а угол или площадь – нет).

Примем сформулированное свойство без доказательства, поскольку доказательство для общего случая (для произвольных линейных элементов) использует понятие преобразования подобия, предлагаемого к изучению в IX классе. Следует отметить, что никакие из сформулированных ниже теорем не опираются на данное свойство.

2. Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.

Пусть треугольники ABC и A₁B₁C₁ подобны с коэффициентом k (рисунок 2). Докажем, что 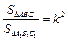. Поскольку углы подобных треугольников попарно равны, ÐA = ÐA₁, и по теореме об отношении площадей треугольников, имеющих по равному углу, 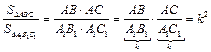(здесь учтено, что в силу подобия ). #

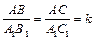Замечание: В IX классе будет дано определение подобия произвольных фигур. Сформулированные выше свойства подобных треугольников останутся справедливыми и для произвольных фигур.

2. Первый признак подобия треугольников.

Выше было сказано, что требования, предъявленные к подобным треугольникам определением (равенство углов и пропорциональность сторон) являются избыточными. Сформулированы и доказаны признаки подобия треугольников, позволяющие устанавливать подобие треугольников по меньшему количеству элементов. В решении задач чаще всего используется первый признак подобия треугольников, утверждающий, что для подобия двух треугольников достаточно равенства их углов:

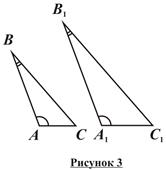
I признак подобия треугольников (по двум углам): Если два угла одного треугольника соответственно равны двум углам второго треугольника, то эти треугольники подобны (рисунок 3).

Дано :

ΔABC, ΔA₁B₁C₁;

ÐA = ÐA₁, ÐB = ÐB₁.

Доказать: ΔABC ~ ΔA₁B₁C₁.

Доказательство:

1. По теореме о сумме углов треугольника ÐC = 180° ‑ (ÐA + ÐB) = 180° ‑ (ÐA₁ + ÐB₁) = ÐC₁.

2. По теореме об отношении площадей треугольников, имеющих по равному углу,
.

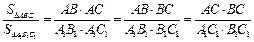3. Из равенства 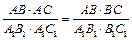следует, что

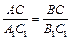, а из равенства 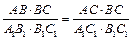‑ что 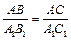. Таким образом, у треугольников ABC и A₁B₁C₁ ÐA = ÐA₁, ÐB = ÐB₁, ÐC = ÐC₁, и 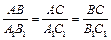, то есть сходственные стороны пропорциональны. А значит, ΔABC ~ ΔA₁B₁C₁ по определению. #

3. Теорема о пропорциональных отрезках. Деление отрезка в заданном отношении.

Теорема о пропорциональных отрезках является обобщением теоремы Фалеса. Напомним, что для использования теоремы Фалеса необходимо, чтобы параллельные прямые, пересекающие две данные прямые, отсекали на одной из них равные отрезки. Обобщенная же теорема Фалеса утверждает, что если параллельные прямые пересекают две данные прямые, то отрезки, отсекаемые ими на одной прямой, пропорциональны отрезкам, отсекаемым на второй прямой. Теорема о пропорциональных отрезках доказывается аналогично теореме Фалеса (только вместо равенства треугольников здесь используется их подобие).

Теорема о пропорциональных отрезках (обобщенная теорема Фалеса): Параллельные прямые, пересекающие две данные прямые, отсекают на них пропорциональные отрезки.

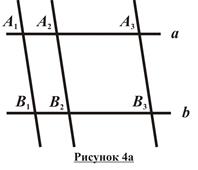Дано :

прямые a, b;

A₁, A₂, A₃Ìa;

B₁, B₂, B₃Ìb;

A₁B₁ïêA₂B₂ïêA₃B₃.

Доказать: .

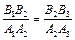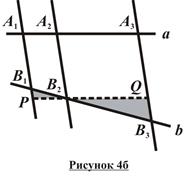
Доказательство: Рассмотрим два случая: aïêb (рисунок 4а) и aÇb (рисунок 4б):

a ï ê b :

1. A₁A₂B₂B₁, A₂A₃B₃B₂ – параллелограммы по определению, Þ по свойству противоположных сторон параллелограмма A₁A₂ = B₁B₂, A₂A₃ = B₂B₃, и равенство 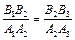верно.

a Ç b:

2. Проведем через точку B₂ прямую PQïêa: PÎA₁B₁, QÎA₃B₃. Тогда по св-ву противоположных сторон п/г PB₂ = A₁A₂, B₂Q = A₂A₃.

3. DB₁B₂P ~ DB₃B₂Q по двум углам (ÐB₁B₂P=ÐB₃B₂Q как вертикальные, ÐB₁PB₂=ÐB₃QB₂ как внутр. н/л при A₁B₁ïêA₃B₃ и секущей PQ); Þ по определению подобных треугольников 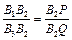. Подставив в полученную пропорцию A₁A₂, вместо B₂P, и A₂A₃ вместо B₂Q (смотри п. 2), получим: 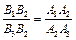. Поменяем местами средние члены пропорции: . #

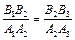Замечание: Доказательство теоремы о пропорциональных отрезках легко обобщить на произвольное количество пар отрезков.

Покажем, как с использованием обобщенной теоремы Фалеса поделить отрезок в заданном отношении:

Пусть заданы отрезок AB и натуральные числа m и n. Необходимо найти на отрезке AB такую точку M, чтобы AM:MB = m:n.

Дано:

отрезок AB;

m, n Ì N.

Построить: т. MÎAB:

AM:MB = m:n.

Построение:

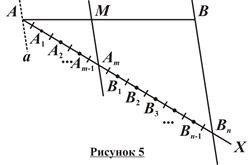
1. Проведем из точки A луч AX так, чтобы угол BAX не был развернутым (рисунок 5). Выберем отрезок произвольной длины d и отложим на луче AX отрезки AA₁ = A₁A₂ = … = A_m-1A_m = A_mB₁ = B₁B₂ = … =
= B_n-1B_n = d.

2. Соединим точки B и B_n и проведем через точку A_m прямую A_mMïêBB_n так, чтобы MÎAB.

3. Точка M – искомая: aïêA_mMïêBB_n, Þ по теореме о пропорциональных отрезках 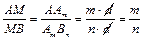(понятно, что проводить через точку A прямую aïêA_mM необязательно). #

4. Свойство медиан треугольника. Ключевая задача о медианах треугольника.

Первый признак подобия треугольников позволяет доказать свойство медиан треугольника:

Свойство медиан треугольника: Медианы треугольника пересекаются в одной точке, называемой центроидом треугольника, и делятся этой точкой в отношении 2:1, считая от вершины (рисунок 6).

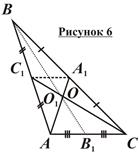Дано:

ΔABC;

AA₁, BB₁, CC₁ – медианы;

AA₁ÇCC₁ = O.

Доказать: BB₁ÇCC₁ = O;

.

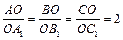Доказательство:

1. Проведем среднюю линию A₁C₁. По теореме о средней линии треугольника A₁C₁ïêAC, и .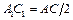

2. DAOC ~ DA₁OC₁ по двум углам (ÐAOC = ÐA₁OC₁ как вертикальные, ÐOAC = ÐOA₁C₁ как внутр. н/л при A₁C₁ïêAC и секущей AA₁); Þ по определению подобных треугольников .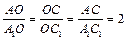

3. Пусть BB₁ÇCC₁ = O₁. Аналогично пунктам 1 и 2 можно доказать, что 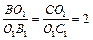. Но поскольку на отрезке CC₁ существует единственная точка O,

делящая его в отношении CO:OC₁=2:1, точки O и O₁ совпадают. А значит, все медианы треугольника пересекаются в одной точке, делящей каждую из них в отношении 2:1, считая от вершины. #

При изучении темы «площади многоугольников» были сформулированы и доказаны три факта о равновеликих треугольниках в фигурах. В частности, было показано, что медиана разбивает произвольный треугольник на две равновеликие части. Оказывается, при пересечении трех медиан треугольника образуется шесть равновеликих треугольников. Назовем этот факт ключевой задачей о медианах треугольника:

Ключевая задача о медианах треугольника: Медианы произвольного треугольника разбивают его на шесть равновеликих треугольников (рисунок 7).

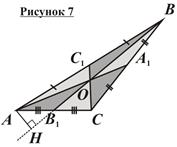Дано: ΔABC; AA₁, BB₁, CC₁ – медианы;

AA₁ÇBB₁ = BB₁ÇCC₁ = O.

Доказать: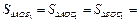

.

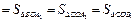Доказательство:

1. Обозначим 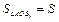. Тогда поскольку OB₁ – медиана треугольника AOC, .

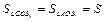2. AH – общая высота треугольников AOB₁ и AOB, Þ 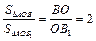по свойству медиан треугольника, Þ S_ΔAOB = 2S.

3. Т.к. OC₁ – медиана треугольника AOB, .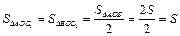

4. Аналогично доказывается, что 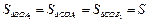. Итак, . #

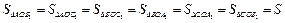5. Второй признак подобия треугольников. Ключевая задача о высотах треугольника.

Второй признак подобия треугольников (по двум сторонам и углу между ними): Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, заключенные между этими сторонами, равны, то треугольники подобны (рисунок 8).

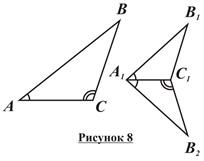Дано : ΔABC, ΔA₁B₁C₁;

ÐA = ÐA₁; .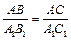

Доказать: ΔABC ~ ΔA₁B₁C₁.

Доказательство:

1. Построим ΔA₁B₂C₁: ÐA₁C₁B₂ = ÐC, ÐC₁A₁B₂ = ÐA = ÐC₁A₁B₁. Тогда ΔABC ~ ΔA₁B₂C₁ по двум углам, Þ по определению подобных треугольников, .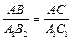

2. По условию, 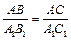; из пункта 1 .

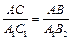Объединяя эти равенства, получим: 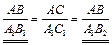, Þ A₁B₁ = A₁B₂.

3. ΔA₁B₂C₁ = ΔA₁B₁C₁ по двум сторонам и углу между ними: A₁C₁ – общая, A₁B₁ = A₁B₂ из пункта 2, ÐC₁A₁B₂ = ÐC₁A₁B₁ по построению; Þ по определению равных треугольников, ÐA₁C₁B₂ = ÐA₁C₁B₁.

4. Итак, ÐA = ÐC₁A₁B₁ по условию, ÐC = ÐA₁C₁B₂ = ÐA₁C₁B₁ из доказанного; Þ ΔABC ~ ΔA₁B₁C₁ по двум углам. #

Второй признак подобия треугольников позволяет доказать факт, значительно облегчающий решение некоторых задач, который мы назовем ключевой задачей о высотах треугольника:

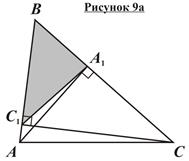
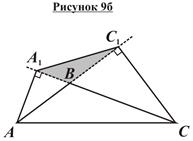
Ключевая задача о высотах треугольника: Если AA₁ и CC₁ – высоты треугольника ABC, то треугольник A₁BC₁ подобен треугольнику ABC (рисунки 9а и 9б).

Дано: ΔABC;

AA₁, CC₁ – высоты ΔABC.

Доказать: ΔABC ~ ΔA₁BC₁.

Доказательство: На рисунках 9а и 9б представлены случаи, соответствующие острому и тупому углам B соответственно. Сразу отметим, что если угол B прямой, то основания высот A₁ и C₁ совпадут с вершиной B, и треугольник A₁BC₁ «превратится» в точку.

1. ΔAA₁B ~ ΔCC₁B по двум углам (ÐAA₁B = ÐCC₁B = 90°; в случае а угол при вершине B – общий, в случае б ÐABA₁ = ÐCBC₁ как вертикальные); Þ по определению подобных треугольников 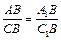Û .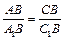

2. ΔABC ~ ΔA₁BC₁ по двум сторонам и углу между ними (в случае а угол при вершине B – общий, в случае б ÐABC = ÐA₁BC₁ как вертикальные; 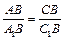из пункта 1). #

Замечание: Следует обратить внимание на порядок вершин подобных треугольников ABC и A₁BC₁: если вершины одного из них обходятся по часовой стрелке, то вершины второго – против часовой стрелки.

При решении задач второй признак подобия, как правило, используется в сочетании с первым признаком подобно тому, как это было сделано в решении ключевой задачи о высотах. То есть сначала с использованием первого признака доказывается подобие треугольников, из которого делается вывод о пропорциональности сторон; затем, пользуясь полученной пропорциональностью сторон, доказывается подобие другой пары треугольников, опираясь на второй признак.

6. Третий признак подобия треугольников.

Третий признак подобия треугольников довольно редко используется в решении задач, а доказательство его аналогично доказательству второго признака.

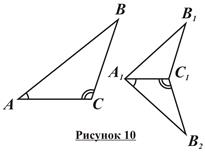Третий признак подобия треугольников (по трем сторонам): Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники подобны (рисунок 10).

Дано: ΔABC, ΔA₁B₁C₁;

.

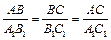Доказать: ΔABC ~ ΔA₁B₁C₁.

Доказательство:

1. Построим ΔA₁B₂C₁: ÐA₁C₁B₂ = ÐC, ÐC₁A₁B₂ = ÐA. Тогда ΔABC ~ ΔA₁B₂C₁ по двум углам, Þ по определению подобных треугольников, .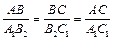

2. По условию, 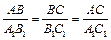; из пункта 1

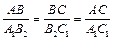. Объединяя эти равенства, получим: 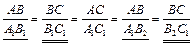, Þ A₁B₁ = A₁B₂, B₁C₁ = B₂C₁.

3. ΔA₁B₂C₁ = ΔA₁B₁C₁ по трем сторонам: A₁C₁ – общая, A₁B₁ = A₁B₂ и B₁C₁ = B₂C₁ из пункта 2; Þ по определению равных треугольников, ÐB₁A₁C₁ = ÐB₂A₁C₁ = ÐA.

4. Итак, ÐA = ÐB₁A₁C₁, 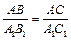по условию; Þ ΔABC ~ ΔA₁B₁C₁ по двум сторонам и углу между ними. #

7. Средние пропорциональные отрезки в прямоугольном треугольнике.

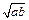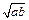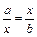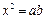Введем понятие среднего пропорционального двух положительных чисел: Средним пропорциональным (средним геометрическим) двух положительных чисел a и b называется число . Название «среднее пропорциональное» связано с тем, что является средним членом пропорции, крайние члены которой положительны и равны a и b, а средние члены совпадают: , Þ Û .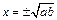

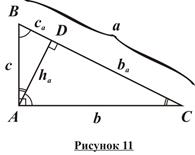Оказывается, при проведении высоты к гипотенузе прямоугольного треугольника (рисунок 11) образуется 3 подобных треугольника, в результате чего образованные в треугольнике отрезки связаны замечательными соотношениями. Эти соотношения устанавливает теорема о средних пропорциональных отрезках в прямоугольном треугольнике:

· Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное проекций катетов на гипотенузу.

· Катет прямоугольного треугольника есть среднее пропорциональное гипотенузы и проекции этого катета на гипотенузу.

Дано : ΔABC; ÐA = 90°;

AD – высота.

Доказать: ;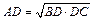

.

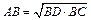Доказательство:

1. По теореме о сумме углов треугольников ÐB = 90° ‑ ÐBAD = ÐCAD.

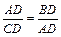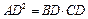2. ΔABD ~ ΔCAD по двум углам (ÐB = ÐCAD, ÐADB = ÐCDA = 90°); Þ по определению подобных треугольников, ; Þ ; Þ .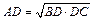

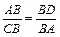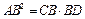3. ΔABD ~ ΔCBA по двум углам (ÐB – общий, ÐADB = ÐCAB = 90°); Þ по определению подобных треугольников, ; Þ ; Þ . #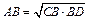

Следствие: Проекции катетов прямоугольного треугольника на гипотенузу пропорциональны квадратам соответствующих катетов (рисунок 11).

Дано : ΔABC; ÐA = 90°;

AD – высота.

Доказать: .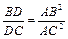

Доказательство:

По теореме о средних пропорциональных отрезках в прямоугольном треугольнике, 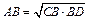, Þ 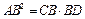. Аналогично 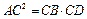. Тогда . #

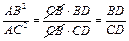Итак, в прямоугольном треугольнике выполняются следующие соотношения (рисунок 11):

;

;

;

;

.
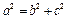
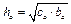
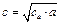
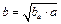
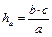