Решение прикладных задач
| 1 вариант | 2 вариант |
1. Тело движется вверх по закону 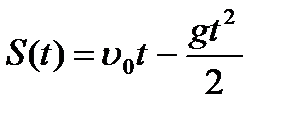 с начальной скоростью с начальной скоростью 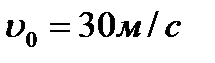 , , 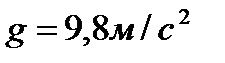 . Через сколько секунд скорость станет равной . Через сколько секунд скорость станет равной 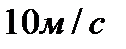 ? ?
| 1. Тело движется вверх по закону 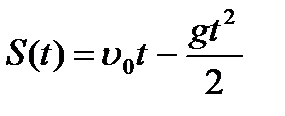 с начальной скоростью с начальной скоростью 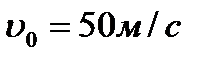 , , 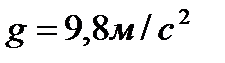 . Через сколько секунд скорость станет равной . Через сколько секунд скорость станет равной 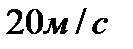 . .
|
2. Найдите силу, действующую на тело массой 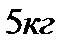 , движущееся по закону , движущееся по закону 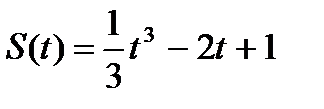 в момент времени в момент времени 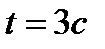 . .
| 2. Тело массой 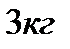 движется по прямой согласно уравнению движется по прямой согласно уравнению 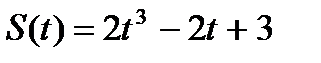 . Найдите действующую на него силу в момент времени . Найдите действующую на него силу в момент времени 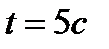 . .
|
3. Определить кинетическую энергию точки, массой 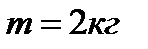 , движущейся по закону , движущейся по закону 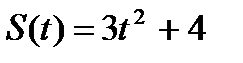 в момент времени в момент времени 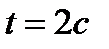 . .
| 3. Определить кинетическую энергию точки, массой 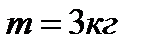 , движущейся по закону , движущейся по закону 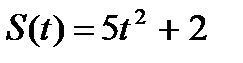 в момент времени в момент времени 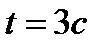 . .
|
4.Точка движется по прямой по закону 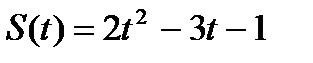 . Найти ускорение точки в момент времени . Найти ускорение точки в момент времени 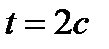 . .
| 4. Точка движется по прямой по закону 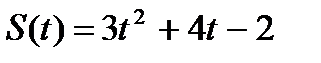 . Найти ускорение точки в момент времени . Найти ускорение точки в момент времени 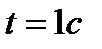 . .
|
3.10. Самостоятельные работы по разделу
«Интеграл и его применение»
1. Решение задач по теме: «Производная». Преобразование.
2. Найти производную функцию.
3. Доклад. Приближенные вычисления.
4. Сообщение/реферат. Таблица производных.
5. Решение задач. Основные свойства интеграла.
6. Определение первообразной.
7. Решение задач. Формула Ньютона — Лейбница.
8. Тема рефератов (докладов), индивидуальных проектов. Понятие дифференциала и его приложения.
Самостоятельная работа № 1
Решение задач по теме: «Производная». Преобразования
№1. Найти производную функции: 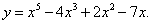
Самостоятельная работа № 2
Найти производную функцию
№1. Найти производную функции в точке 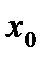 :
:
а) 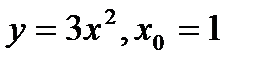 ;
;
б) 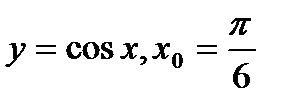 ;
;
в) 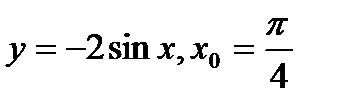 ;
;
с)  .
.
Самостоятельная работа № 3
Доклад. Приближенные вычисления
Форма самостоятельной деятельности: подготовить доклад по предложенной теме.
Самостоятельная работа № 4
Сообщение/реферат. Таблица производных.
Форма самостоятельной деятельности: подготовить сообщение по предложенной теме.
Самостоятельная работа № 5
Решение задач. Основные свойства интеграла.
№1. Вычислите:
а) 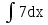
б) 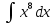
в) 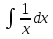
Самостоятельная работа № 6
Определение первообразной.
№1. Найдите первообразную для следующих функций:
а) f(x) = 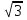
б) f(x) = 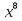
Самостоятельная работа № 7








