Решение задач по теме: «Векторы. Преобразование выражений»
Выполните задания:
| № п/п | Название операции | Формулы |
| 1 | Найти сумму векторов | 
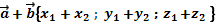
|
| 2 | Найти разность векторов | 
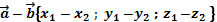
|
| 3 | Найти произведение вектора на число | 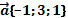 , , 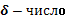 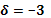

|
| 4 | Вычислить координаты середины отрезка | Точка A 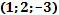 . Точка B (-3;4;-1 . Точка B (-3;4;-1 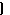 .Точка С- середина отрезка АВ. С( .Точка С- середина отрезка АВ. С( 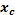 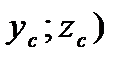  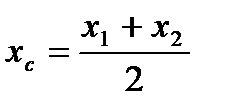 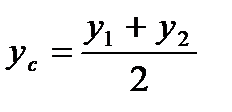 ; ; 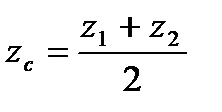 . .
|
| 5 | Найти координаты вектора | Точка A 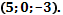 Точка B (-1;4;-7 Точка B (-1;4;-7  .Находим координаты вектора .Находим координаты вектора 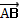 . Из координат конца вычислить координаты начала вектора . Из координат конца вычислить координаты начала вектора
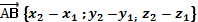
|
Самостоятельная работа № 2
Построение векторов
№1. Найдите координаты середины отрезка АВ, если А(-2;3), В(6;-3)
№2. Найдите длину отрезка ЕН, если Е(-3;8), Н(2;-4)
№3. Найдите длину вектора 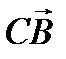 {-4; -3}
{-4; -3}
№4. Вершины ∆АВС имеют координаты А(8;-3), В(5;1), С(12;0). Докажите
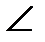 В=
В= 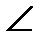 С. Найдите S∆АВС
С. Найдите S∆АВС
№5. Найдите длину вектора 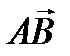 ,если А(3;-6),В(-4; -7).
,если А(3;-6),В(-4; -7).
Самостоятельная работа № 3
Построение векторов в пространстве
№1.Даны векторы: а ⃗ =3ι ⃗ + 2ϳ ⃗ - 5к ⃗ в ⃗ = -2ι ⃗ + 3ϳ ⃗ + 4к ⃗ . Вычислите координаты векторов а ⃗+в ⃗ ; 2а ⃗ и постройте их.
№2. Даны векторы: а ⃗{2;2;-1} в ⃗{-3;6;-6}. Найдите: cos(а ⃗ в ⃗)
№3. Докажите, что четырехугольник с вершинами А(1;4;3) В(2;3;5) С(2;5;1) Д(3;4;3)-параллелограмм.
Самостоятельная работа № 4
Определение скалярного произведения векторов
№1. Вычислите скалярное произведение векторов 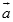 и
и 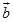 , если
, если 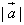 = 2,
= 2, 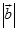 = 3, а угол между ними равен 120°.
= 3, а угол между ними равен 120°.
№2. Вычислите скалярное произведение векторов 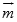 и
и 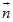 , если
, если 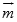 {3; –2},
{3; –2}, 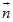 {–2; 3}.
{–2; 3}.
№3. Вычислите косинус угла между векторами 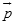 и
и 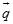 , если
, если 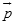 {3; –4},
{3; –4}, 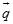 {15; 8}.
{15; 8}.
№4. Даны векторы 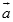 {2; –3} и
{2; –3} и 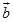 {х; –4}. При каком значении х эти векторы перпендикулярны?
{х; –4}. При каком значении х эти векторы перпендикулярны?
№5. Найдите угол между ненулевыми векторами 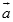 {х; у} и
{х; у} и 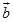 {–у; х}.
{–у; х}.
Самостоятельная работа № 5
Реферат (доклад), индивидуальный проект. Тема: «Векторное задание прямых и плоскостей в пространстве».
Форма самостоятельной деятельности: подготовить реферат по предложенной теме.
3.6. Самостоятельные работы по разделу «Основы тригонометрии»
1. Нахождение значений тригонометрических функций.
2. Нахождение значений тригонометрических функций.
3. Упростить, выражения используя, формулы приведения и сложения тригонометрических функций.
4. Решить уравнение. Действия с обратными тригонометрическими функциями
5. Решение простейших тригонометрических уравнений.
6. Решение простейших тригонометрических неравенств.
7. Реферат (доклад), индивидуальный проект. Тема «Сложение гармонических колебаний».
ДОПОЛНИТЕЛЬНЫЕ САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
8. Решение тригонометрических уравнений повышенной сложности.








