Решение задач по теме: «Признаки делимости»
Вариант 1
1) Какие из чисел 23478, 2355, 105600, 3421, 7775, 20000, 39717 делятся:
а) на 2, б) на 5, в) на 10.
2) Какие четные числа удовлетворяют неравенству: 231  х
х  238
238
3) В числе 234* замените * цифрой так, чтобы полученное число:
а) делилось на 5, но не делилось на 10,
б) делилось на 2, но не делилось на 5,
в) делилось на 2 и на 5,
г) не делилось ни на 2, ни на 5
Вариант 2
1) Какие из чисел 54783, 45000, 84855, 9871, 900460, 1115, 567896 делятся:
а) на 2, б) на 5, в) на 10.
2) Какие нечетные числа удовлетворяют неравенству: 432  х
х  439
439
3) В числе 753* замените * цифрой так, чтобы полученное число:
а) делилось на 5, но не делилось на 10,
б) делилось на 2, но не делилось на 5,
в) делилось на 2 и на 5,
г) не делилось ни на 2, ни на 5
Самостоятельная работа № 2
Решение задач по теме: «Нахождение наименьшего общего кратного и наибольшего общего делителя»
Решите текстовые задачи с помощью НОК и НОД чисел:
№1. Туристы проехали за 1 день 56 км, а за 2 дня 72км, причем их скорость была одинаковой и выражалась целым числом км/ч, и каждый день они были в пути целое число часов. Найдите скорость, с которой ехали туристы, если она была наибольшей из удовлетворяющих условию задачи.
№2. На столе лежат книги, число которых меньше, чем 100. Сколько лежит книг, если известно, что их можно связывать пачки по 3, по 4, и по 5 штук?
№3. Теплоход «Суворов» свой рейс туда и обратно совершает за 8 дней, теплоход «Горький» за 12 дней, а теплоход «Киров» за 18 дней. Через сколько дней теплоходы снова встретятся в порту, если они ушли в рейс одновременно?
№4. В детском велосипеде шестерня заднего колеса имеет 21 зубец, а шестерня педали 44 зубца. Какое наименьшее число оборотов должна сделать педаль, чтобы шестерни вернулись в свое первоначальное положение?
№5. Два автобуса одновременно отправляются от одной площади по разным маршрутам. У одного рейс туда и обратно длится 48 минут, а у другого 1 час 12 минут. Через сколько времени автобусы снова встретятся на этой площади?
Самостоятельная работа № 3
Решение задач по теме: «Действия с дробями»
Вариант №1
1. Представьте 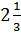 в виде неправильной дроби.
2. Выделите целую часть числа в виде неправильной дроби.
2. Выделите целую часть числа 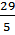 .
3. Выполните действия:
а) .
3. Выполните действия:
а) 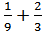 ; в) ; в) 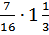 ;
б) ;
б) 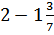 ; г) ; г) 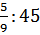 ;
4. В олимпиаде участвовало 300 школьников, ;
4. В олимпиаде участвовало 300 школьников,  из них прошли в следующий тур. Сколько школьников будут проходить испытания в следующем туре олимпиады?
5. В одном ящике из них прошли в следующий тур. Сколько школьников будут проходить испытания в следующем туре олимпиады?
5. В одном ящике 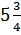 кг огурцов, а в другом – в 2 раза больше. Сколько килограммов огурцов в двух ящиках?
6. Аня может прополоть грядку за 2 часа, а Влад – за 3 часа. За какое время они прополют грядку, работая совместно?
7. кг огурцов, а в другом – в 2 раза больше. Сколько килограммов огурцов в двух ящиках?
6. Аня может прополоть грядку за 2 часа, а Влад – за 3 часа. За какое время они прополют грядку, работая совместно?
7. 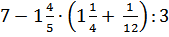
| Вариант №2
1. Представьте 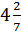 в виде неправильной дроби.
2. Выделите целую часть числа в виде неправильной дроби.
2. Выделите целую часть числа  .
3. Выполните действия:
а) .
3. Выполните действия:
а) 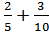 ; в) ; в) 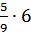 ;
б) ;
б) 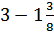 ; г) ; г) 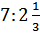 ;
4. В поход отправились 24 пятиклассника, ;
4. В поход отправились 24 пятиклассника,  из них – мальчики. Сколько мальчиков пошли в поход?
5. Рома собрал из них – мальчики. Сколько мальчиков пошли в поход?
5. Рома собрал 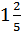 кг ягод, а мама – в 5 раза больше. Сколько килограммов ягод они собрали вместе?
6. Расстояние от дома до летнего лагеря велосипедист проезжает за 3 часа, а пешеход проходит за 6 часов. Они отправились из этих двух пунктов навстречу друг другу одновременно. Через сколько часов они встретятся?
7. кг ягод, а мама – в 5 раза больше. Сколько килограммов ягод они собрали вместе?
6. Расстояние от дома до летнего лагеря велосипедист проезжает за 3 часа, а пешеход проходит за 6 часов. Они отправились из этих двух пунктов навстречу друг другу одновременно. Через сколько часов они встретятся?
7. 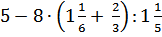
|
Самостоятельная работа № 4
Разработать презентацию: «Модуль числа»
№1. Укажите значение выражения|-2,3|:
а) -2,3; б)-3,2; в)3,2; г)2,3.
№2. Найдите модуль числа:
а) +36; б)-1,78; в) 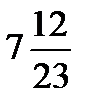 ; г)-478.
; г)-478.
№3. Сравните:
а) |-2,3| и 0; б) |-56,2| и 26; в) |-75,2| и 75,2; г) |-12| и |-28|.
№4. Вычислите:
а) |-26|-|-14|+|+18|; б) |-13,2|+|+8,9|-|-10,1|;
в) |-3,8|·|-2,2|·|+2|; г) |-65,6|:|-1,6|:|+0,41|.
№5. Решите уравнение:
а) |x|=14; б) |x|+9,25=11,83;
в) 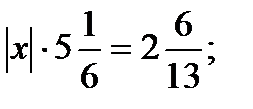 г)
г) 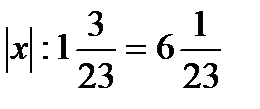 .
.
Самостоятельная работа № 5








