7,8,11. Понятие «геометрического фактора» в теории методов радиометрии скважин

Дата: 2025-04-30; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Геометрический фактор пласта показывает – какая часть пространства (скважина, пласт) влияет на показания.

Для необсаженной скважины:

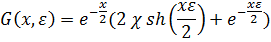
Где e - эксцентриситет прибора, c - метрологическая характеристика прибора.

Если прибор прижат к стенке скважины, то геометрический фактор рассчитывается по формуле:

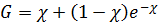
В этом случае 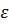равен 1.

 

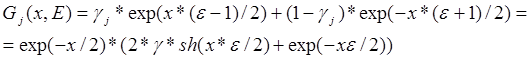
,где γ или ϰ (в учебниках Кожевникова «альбедо») - геометрический фактор полупространства (относительный вклад излучения полупространства, определяется экспериментально, не зависит от типов излучателей, но для утяжелённых растворов зависит от плотности), а E - эксцентриситет; 0<E>1

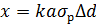
k- коэффициент приведения к нормальной среде; a – радиальная чувствительность прибора; 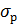– плотность бурового раствора;

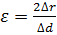
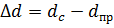
dс и dпр – диаметры скважины и прибора; 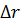– расстояние между осями прибора и скважины.

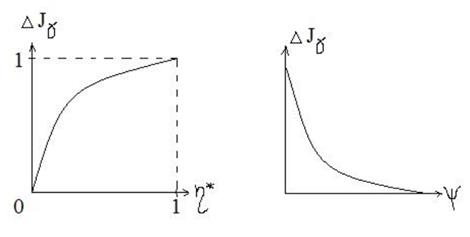
Величина 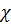имеет смысл относительного вклада излучения полупространства со свойствами породы. В случае обсаженной скважины необходимо вычислять геометрические факторы каждой зоны для каждого излучателя. Зависимость геометрического фактора от положения прибора в скважине и от параметра промежуточной зоны

 

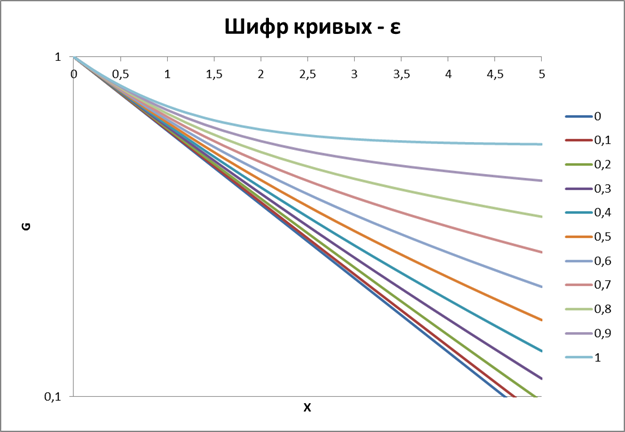
Для интерпретации необходимо показания, зарегистрированные в нестандартных условиях, привести к стандартным (dc=20 см, dп=9 см, σр= 1 г/см3 ).

Построение поправочных палеток

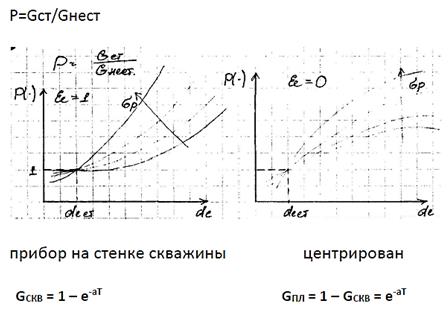
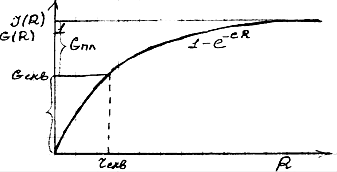кривая радиального насыщения

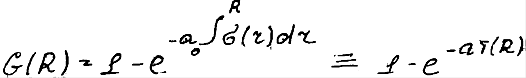
T(R) – оптическая толщина промежуточных зон.

 

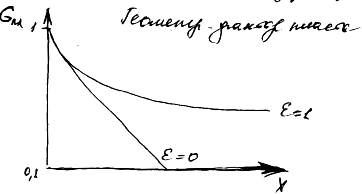
а) На зависимости геометрического фактора от положения прибора в скважине и от параметра промежуточной зоны видна горизонтальная асимптота, к которой стремятся все графики, это говорит о том, что прибор всегда «чувствует» часть пласта (примерно 50% вклада в сигнал).

б) Геометрический фактор монотонно убывает с расстоянием по экспоненте. Скорость убывания и эксцентриситет прибора находятся в обратной зависимости. Геометрический вклад скважины в суммарные показания прибора снижается за счёт уменьшения толщины слоя промывочной жидкости между прибором и стенкой скважины.

 

9. Прямая и обратная задачи, теория интерпретационно-метрологического обеспечения метода естественной радиоактивности в интегральной и спектрометрической модификациях

10. Теория интерпретационной модели ГМ. Петрофизическая модель ГМ

Для интегрального ГМ:

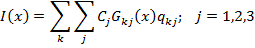
x – совокупность переменных параметров, характеризующих условия измерений

k – номер зоны

j – номер излучателя

Cj – концентрационная чувствительность прибора

qkj – массовая концентрация

Возможность количественной интерпретации данных интегрального ГМ – оценка суммарного содержания ЕРЭ.

Интерпретационный параметр – безразмерная величина, двойной разностный параметр:

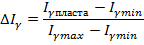
Этот параметр исключает возможность анализа абсолютного уровня радиоактивности и не имеет никакого петрофизического смысла. Поэтому для оценок глинистости по ГМ используются эмпирические зависимости, если их удаётся предварительно установить с помощью лабораторных исследований на образцах горных пород.

Входные данные:

 

  1. концентрационная чувствительность по урану;
  2. радиальная чувствительность;
  3. текущая статическая амплитуда показаний (имп/мин или мР/час);
  4. плотность промывочной жидкости (г/см3) и её тип (обычный глинистый раствор или утяжелённый баритом);
  5. текущий диаметр скважины (данные кавернометрии);
  6. плотность и толщина стенки обсадной колонны;
  7. плотность и толщина глинистой корки;
  8. плотность цементного камня;
  9. скорость v регистрации диаграмм (м/час) и постоянная времени t интегрирующей ячейки (с) (при её наличии).


Величины v и t вводятся для преобразования динамических аномалий в статические. Параметры промежуточных зон используются при определении геометрических факторов зон в системе скважина-пласт (для обсаженных скважин плотность цементного камня вводится по умолчанию; при некачественном цементировании возможна корректировка).

Чтобы определить суммарное содержание ЕРЭ в изучаемом пласте в единицах eU, надо определить абсолютную аномалию I(x), выделив из сигнала J(x) фоновую компоненту:

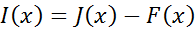
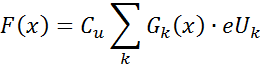
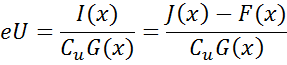
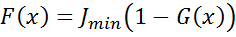
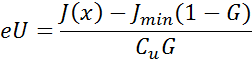
Суммарное массовое содержание ЕРЭ зависит от объёмных содержаний всех контрастных по р/а компонент породы.

12. Количественный учёт влияния скважинных условий на показания ГМ

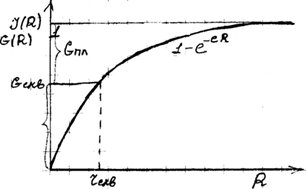Кривая радиального насыщения (R – радиус цилиндрической зоны среды).

Эта кривая элементарного пласта описывается уравнением 1-е-еR, но это справедливо, если бы свойства не зависели от радиальной неоднородности. Но от нее зависит плотность.

а – некая произвольная const,

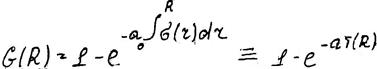σ – плотность породы.

T = σ P Δd /2,

где Δd =dСКВ–dПРИБ – толщина среды, Т – массовая толщина, σ P – σ раствора.

a = - ∂ lnG /∂ T ≡ -1/ G ∂ G /∂ T – радиальная чувствительность прибора. Физ. смысл: определяет относительное изменение геометрического фактора пласта (для центрированного в скважине прибора) при единичном изменении массовой толщины Т.

G СКВ = 1 – e-aT G ПЛ = 1 – G СКВ = e-aT

 

13. Учёт радиоактивности бурового раствора и изменений технических условий измерений при интерпретации данных ГМ

Для расчёта eU по разрезу скважины необходимо знать значения {eUk} урановых эквивалентов промежуточных зон. Эти данные не всегда возможно получить с необходимой точностью. Активность промывочной жидкости в стволе скважины может заметно отличаться от активности промывочной жидкости, измеренной на поверхности.

Можно, например, определять автоматически (программно) и использовать в алгоритме среднее значение уранового эквивалента для объединения промежуточных зон eUf. В этом (простейшем) способе определения фоновой компоненты делаются два допущения:

1) активность промежуточной зоны (или объединения промежуточных зон) такая же, как в пласте с минимальной амплитудой аномалии Jmin;

2) активность промежуточной зоны не изменяется вдоль ствола скважины (величина фоновой компоненты F для каждого пласта при этом будет зависеть, конечно, от текущего диаметра скважины и плотности промывочной жидкости).

Для реализации этого способа в разрезе скважины выбирается пласт с минимальными показаниями Jmin. Тогда

eUf = Jmin/CU ,

и фоновая компонента F(x) текущих показаний определяется через Jmin и текущую величину геометрического фактора промежуточной зоны следующим образом:

F(x) = CU eUf [1-G(x)] = Jmin*[1-G(x)].

Если диаметр скважины и плотность раствора вдоль ствола не изменяются, то фоновая компонента также постоянна.