4, 6. Уравнение переноса излучения в веществе и его приближенные формы
В общем случае, частицы ионизирующего излучения при распространении в веществе обладают различной энергией и перемещаются в различных направлениях. Пространственное, энергетическое и угловое распределения излучения определяются в результате решения кинетического уравнения Больцмана - уравнения переноса излучения в веществе. Коэффициенты этого уравнения являются достаточно сложными функциями энергии и пространственных координат, поэтому точное решение этого уравнения в общем виде не представляется возможным. Вместе с тем, решение большинства практически важных задач можно получить с достаточно высокой степенью точности с помощью использования тех или иных допущений.
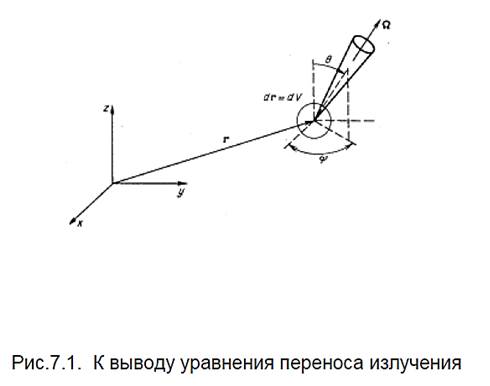
Уравнение переноса излучения описывает баланс частиц в элементе шестимерного фазового пространства координат и импульсов частиц. При расчетах радиационной защиты, как правило, рассматриваются стационарные задачи. Вводятся: радиус-вектор r, определяемый тремя пространственными координатами (рис.7.1); Ω - единичный вектор направления движения частицы; E- энергия частицы. Около точки, определяемой радиус-вектором r, выделяется элементарный объем dr и рассматривается баланс частиц, движущихся в пучке направления dΩ около направления Ω и характеризующихся энергией в интервале от E до E+dE. Тогда ф(r, E, Ω) - дифференциальная (энергетически-угловая) плотность потока частиц в точке r с энергией E и направлением движения Ω.
Изменение числа частиц в элементе фазового пространства drdEdΩ обусловлено следующими факторами:
1. утечкой частиц из рассматриваемого элемента объёма:
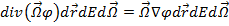
2. убылью частиц в результате их взаимодействия с ядрами среды:
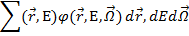
Где Σ(r, E) – полное макроскопическое сечение взаимодействия.
3. излучением источников частиц, имеющих плотность q:
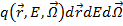
4. приростом числа частиц, вызванного рассеянием:
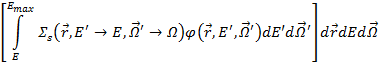
Интегро-дифференциальное уравнение баланса частиц, называемое по аналогии с кинетической теорией газов кинетическим уравнением Больцмана, имеет вид:
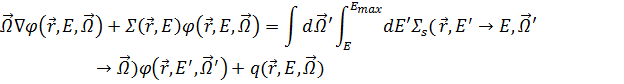
Уравнение получено без учёта квантово-механических эффектов, поляризации частиц при распространении в веществе и в предположении, что плотность потока частиц много меньше плотности ядер вещества.
Важным условием, которое необходимо учитывать при решении уравнения переноса, является условие непрерывности функции ф во всех рассматриваемых точках, в том числе на границах раздела различных материалов (исключая случай наличия поверхностных источников внутри рассматриваемой области).
Решением уравнения Больцмана является дифференциальная плотность потока излучения ф(r,E,Ω).

5. «Уравнение возраста». Фермиевский и полный возрасты нейтронов
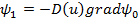
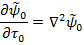
Левая часть уравнения – производная функции плотности замедления по величине возраста нейтронов. Правая часть – оператор Лапласа от функции плотности замедления, т.е. сумма вторых частных производных плотности замедления по координатам.
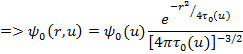
Решение уравнения возраста даёт функцию пространственного и энергетического распределения замедления нейтронов в зависимости от замедляющих свойств среды.

В поглощающей среде возраст нейтронов убывает с возрастанием полной вероятности поглощения. При этом влияние поглощения тем сильнее, Чем выше величина косинуса (u), т.е. при изменении угловой анизотропии рассеяния.








