Определите, какие из чисел являются корнями уравнения. Ответы поясните .
24.02.22
Тема Решение задач
- Актуализация опорных знаний.
1.Повторение теоретического материала по заданной теме
1.Что такое уравнение?
2.Что значит решить уравнения?
3.Какие уравнения называются равносильными?
4.Какие вы знаете равносильные преобразования? (1)если перенести слагаемые из одной части уравнения в другую, изменив его знак; 2) если обе части уравнения умножить или разделить на одно и тоже число, отличное от нуля)
5.Какие уравнения называются рациональными? (Уравнения называются рациональными, если его левая и правая части являются рациональными выражениями.)
6. Какие виды рациональных уравнений вы знаете? ( Целые и дробные)
7. Назовите виды уравнений записанных на доске:
1) 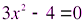 2)
2) 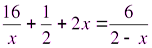 3)
3) 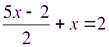 4)
4) 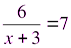
(Целые и дробно-рациональные)
8.Чем отличаются дробные от целых рациональных уравнений (дробные содержат деление на выражение с переменной)
9. Что является корнем дробно-рационального уравнения? (Корнем дробно-рационального уравнения являются числа, обращающие его в верное равенство)
10. Что такое ОДЗ? (ОДЗ - область допустимых значений, то есть это все значения переменной, при которых выражение имеет смысл)
Определите, какие из чисел являются корнями уравнения. Ответы поясните .
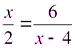
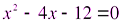
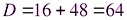
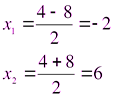
Учащиеся: 4 не может быть корнем, т.к. знаменатель обращает в нуль.
0 не является корнем, т.к. 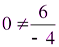 .
.
-2 является корнем, т.к. 
Какие алгоритмы решения дробно-рациональных уравнений вы знаете:
1.
1. Найти общий знаменатель дробей, входящих в уравнение
2. Умножить обе части уравнения на общий знаменатель
3. Решить полученное целое уравнение
4. Исключить из его корней те, которые обращают в нуль знаменатель.
2.
1. Найти ОДЗ уравнения
2. Найти общий знаменатель дробей, входящих в уравнение
3. Умножить обе части уравнения на общий знаменатель
4. Решить полученное целое уравнение
5. Исключить из его корней те, которые обращают в нуль знаменатель.
Записаны решения одного и того же уравнения с использованием различных схем оформления.
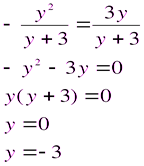
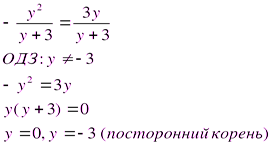
Проверка:
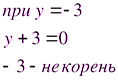
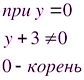 Ответ: 0.
Ответ: 0.
Ответ: 0.
2.Решение упражнений.
а) Найдите общий знаменатель и определите дополнительный множитель каждой дроби.
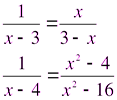
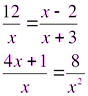
б) Определить какие числа не могут быть корнями уравнений
3. Решение уравнений
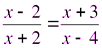
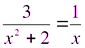
4.В каких задачах мы встречаем дробно- рациональные выражения
В тех, где одна величина выражается через другие при помощи дробного выражения.
Например: время = 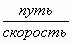 ;
; 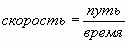 ;
;
Cторона прямоугольника= 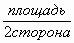 ;
;
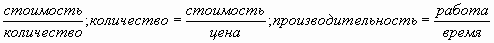 ;
;
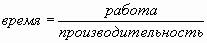 и другие.
и другие.
Сегодня мы затронем три вида задач : на работу, на движение и на совместную работу.
Задача 1:
Члены школьного кружка натуралистов отправились на катере для сбора лекарственных трав. Проплыв вниз по течению реки 35 км, они сделали трехчасовую стоянку, после чего вернулись назад. Определите скорость катера в стоячей воде, если на все путешествие ушло 7 часов, а скорость течения реки 3 км/ч.
| V (км/ч) | t (ч) | S (км) | |
| По течению. | |||
| Против течения. | |||
| Собственная скорость катера | |||
| Скорость течения реки |
Прогнозируемый результат ответа:
Уравнение: 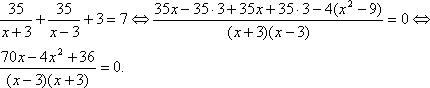
2х  -35х-18=0. Д=1269. х
-35х-18=0. Д=1269. х  =18; х
=18; х  =-
=-  .
.
Ответ: v=18км/ч.
Задача 2:
Токарь должен был обработать 120 деталей к определенному сроку. Применив новый резец, он стал обтачивать в час на 20 деталей больше и поэтому закончил работу на 1 ч раньше срока. Сколько деталей он должен обрабатывать по плану?
| производительность | время | всего | |
| По плану | |||
| Фактически |
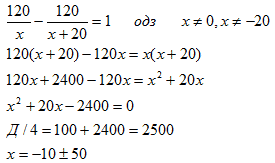
x = 40 или x = -60 не удовлетворяет условию задачи
Ответ: 40 деталей.
Новый тип задач на совместную работу.
Задача 3. Мастер на выполнение заказа тратит определенное количество дней, а ученик потратит на выполнение этого заказа на 10 дней больше. Работая вместе, мастер и ученик могут выполнить заказ за 12 дней. За какое время каждый из них работая отдельно может выполнить заказ.

12(Х+10)+12Х-(х2+10Х)=0
12Х+120+12Х-х2-10Х=0
Х2 -14Х-120=0 Д=196+480=676=26? Х1= 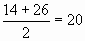
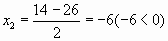
Один из рабочих выполнит работу за 20 дней, а другой за 30 дней.
Ответ: 20 дней и 30 дней.
5. Домашнее задание повт. п. 25,26, решить №690(а,д),629, 698








