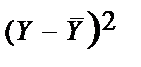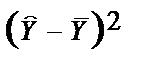І. Побудова моделі
Розглянемо двофакторну лінійну модель 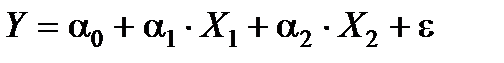 . Оцінимо її параметри на основі МНК. Оцінене рівняння моделі запишемо як
. Оцінимо її параметри на основі МНК. Оцінене рівняння моделі запишемо як 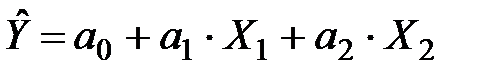 .
.
Система нормальних рівнянь для моделі множинної регресії має вигляд 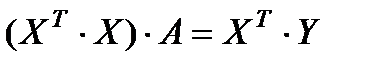 ,
,
звідки
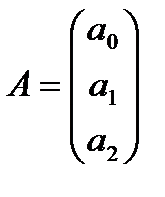 =
= 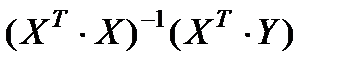 .
.
Виконаємо всі необхідні обчислення. Уведемо матрицю
X= 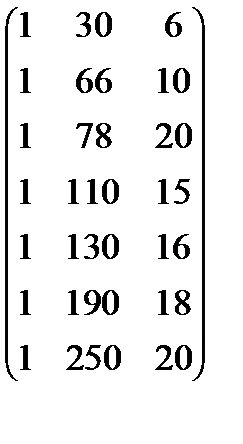 ,
,
тоді
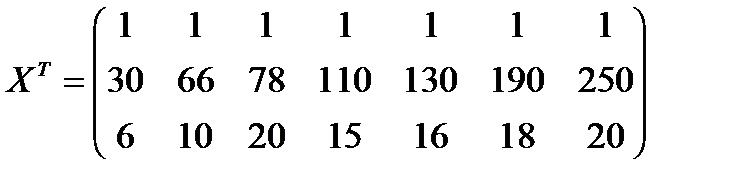 ;
;
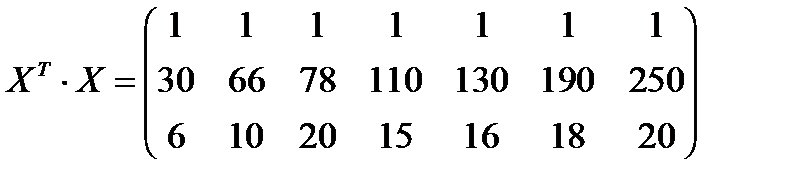 ·
· 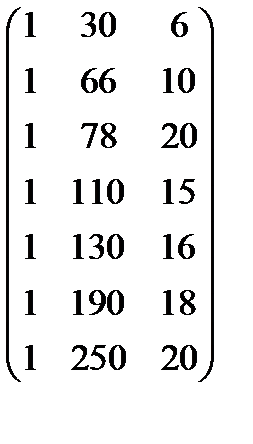 =
=  ;
; 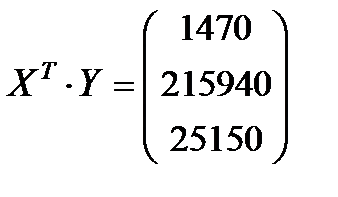 .
.
Запишемо таку систему нормальних рівнянь:
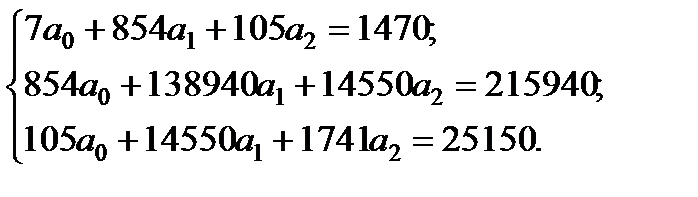
Для розв’язання системи методом оберненої матриці знайдемо таке:
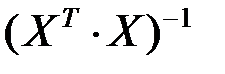 =
= 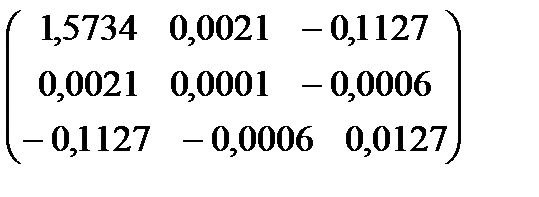 ,
,
звідки
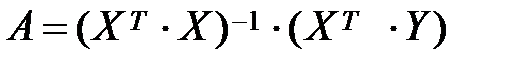 =
= 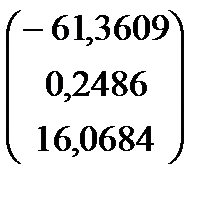 .
.
Отже, рівняння моделі має вигляд
Y = –61,36+0,25x1+16,07x2.
Оцінка параметра 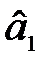 характеризує граничну зміну величини прибутку (Y) залежно від інвестиційних вкладень в оборотні кошти (X1) на одиницю. Тобто якщо інвестиційні вкладення в оборотні кошти зростуть на одиницю, то прибуток збільшиться на 0,25 одиниці за незмінного основного капіталу.
характеризує граничну зміну величини прибутку (Y) залежно від інвестиційних вкладень в оборотні кошти (X1) на одиницю. Тобто якщо інвестиційні вкладення в оборотні кошти зростуть на одиницю, то прибуток збільшиться на 0,25 одиниці за незмінного основного капіталу.
Оцінка параметра 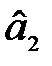 характеризує граничне зростання витрат прибутку (Y) залежно від інвестиційних вкладень в основний капітал (X2). Так, якщо інвестиційні вкладення в основний капітал збільшаться на одиницю, то прибуток зросте на 16,07 одиниці за незмінної величини інвестиційних вкладень в оборотні кошти.
характеризує граничне зростання витрат прибутку (Y) залежно від інвестиційних вкладень в основний капітал (X2). Так, якщо інвестиційні вкладення в основний капітал збільшаться на одиницю, то прибуток зросте на 16,07 одиниці за незмінної величини інвестиційних вкладень в оборотні кошти.
ІІ. Перевірка якості моделі
Зведемо всі показники, необхідні для розрахунку параметрів і характеристик моделі, у табл. 10.
Таблиця 10
| Номер підприємства | Y | X1 | X2 | 
| | | e2 | Точність |
| 1 | 50 | 30 | 6 | 42,51 | 25600 | 28053,27 | 56,12 | 14,98 |
| 2 | 120 | 66 | 10 | 115,73 | 8100 | 8886,12 | 18,20 | 3,56 |
| 3 | 290 | 78 | 20 | 279,40 | 6400 | 4816,57 | 112,33 | 3,65 |
| 4 | 190 | 110 | 15 | 207,02 | 400 | 8,90 | 289,55 | 8,96 |
| 5 | 200 | 130 | 16 | 228,06 | 100 | 326,08 | 787,23 | 14,03 |
| 6 | 300 | 190 | 18 | 275,11 | 8100 | 4239,73 | 619,35 | 8,30 |
| 7 | 320 | 250 | 20 | 322,17 | 12100 | 12581,85 | 4,70 | 0,68 |
| Сума | 1470 | 854 | 105 | 1470 | 60800 | 58912,52 | 1887,48 | 54,15 |
| Середні | 210 | 122 | 15 | – | TSS | ESS | RSS | 7,74% |
1. Перевірка загальної якості моделі
Порівнявши дисперсію залишків і факторну дисперсію, бачимо, що
RSS<ЕSS, тому попередньо можна вважати, що досліджуване рівняння визначає адекватну модель.
Знайдемо коефіцієнт детермінації:
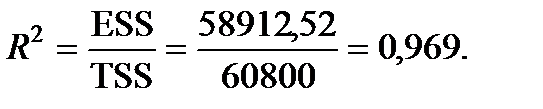
Розрахуємо скоригований коефіцієнт детермінації:
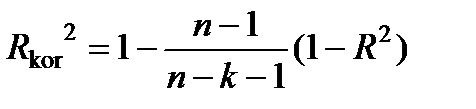 =
= 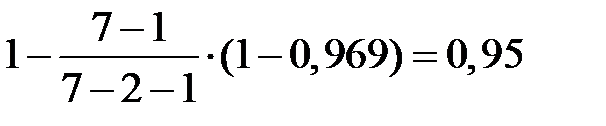 .
.
Обидва коефіцієнти свідчать про сильний зв’язок між факторними змінними та результативним показником. Варіація аналізованої залежної змінної 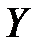 на 95% визначена зміною факторних змінних.
на 95% визначена зміною факторних змінних.
Перевіримо статистичну значущість рівняння в цілому на основі критерію Фішера. Розрахуємо статистику Фішера:
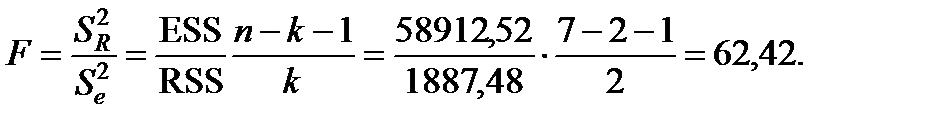
Табличне значення статистики складає Fтабл ( 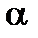 =0,05; 2,4)=6,94.
=0,05; 2,4)=6,94.
Оскільки розрахункове значення статистики F набагато більше критичного значення, можна визнати модель адекватною та надійною з імовірністю 95%.
2. Перевірка статистичної значущості параметрів моделі
Обчислимо коваріаційну матрицю 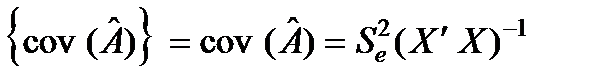 :
:
1) визначимо незміщену оцінку дисперсії залишків 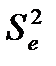 , застосувавши співвідношення
, застосувавши співвідношення
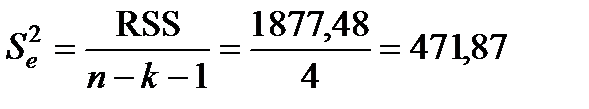 ;
;
2) знайдемо таке:
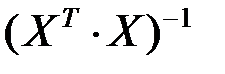 =
= 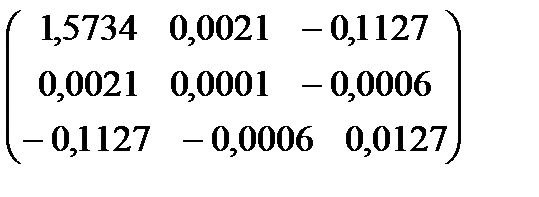 ;
;
3) отримаємо дисперсійно-коваріаційну матрицю
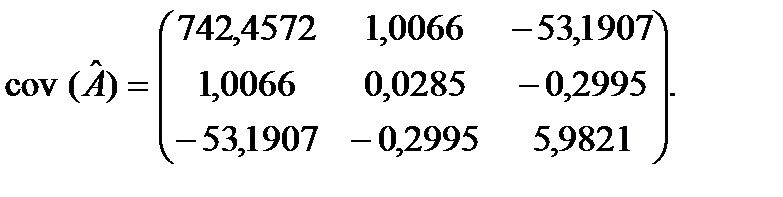
Із матриці визначимо дисперсії оцінок 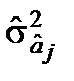 :
:
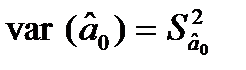 = 742,45;
= 742,45; 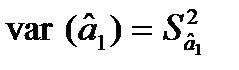 = 0,0285;
= 0,0285; 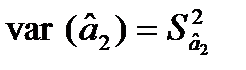 = 5,9821.
= 5,9821.
Коваріації відповідних оцінок параметрів становлять
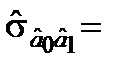 1,0066;
1,0066; 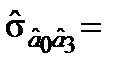 53,1907;
53,1907; 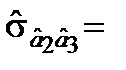 –0,2995.
–0,2995.
Знак «мінус» перед оцінками коваріацій указує на те, що зі збільшенням однієї оцінки параметрів інша зменшується в середньому і навпаки.
Обчислимо стандартні похибки оцінок параметрів моделі:
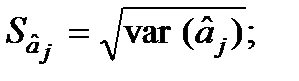
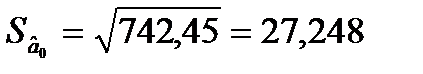 ;
; 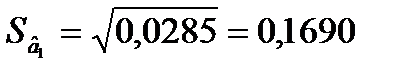 ;
; 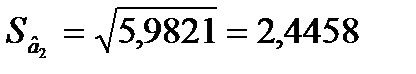 .
.
Стандартні похибки характеризують середні лінійні коливання оцінок параметрів моделі навколо свого математичного сподівання. Чим менші ці похибки, тим більш стійкі оцінки параметрів моделі. Але остаточні висновки стосовно стійкості оцінок можна зробити, порівнявши стандартні похибки з абсолютними значеннями оцінок параметрів моделі. Тому знайдемо 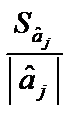 :
:
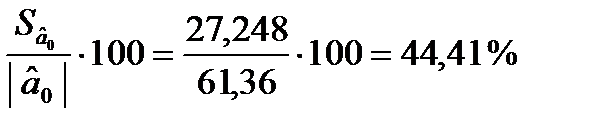 ;
; 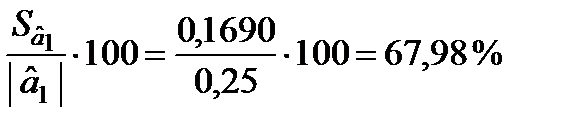 ;
; 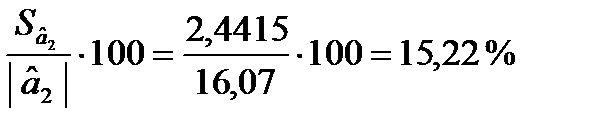 .
.
Отже, стандартні похибки оцінок параметрів відносно рівня самих оцінок становлять відповідно 44,41, 67,98 і 15,22 %, що свідчить про зміщення оцінок. Це означає, що залишки можуть мати систематичну складову, зумовлену неточною специфікацією моделі. Наприклад, не всі основні чинники, які впливають на результативний фактор, внесено до моделі.
Для перевірки статистичної значущості параметрів знайдемо статистики Стьюдента:
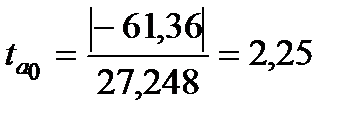 ;
; 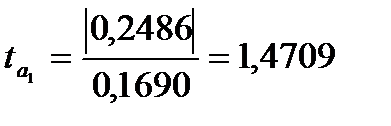 ;
; 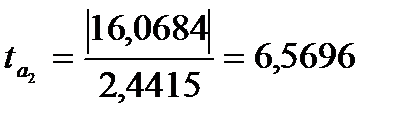 .
.
Теоретичне значення статистики Стьюдента складає
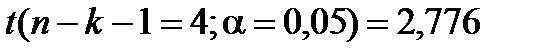 .
.
Для коефіцієнтів 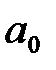 та
та 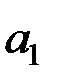 розрахункове значення статистики менше теоретичного, тому гіпотезу про рівність їх нулю відкинути не можна і ці коефіцієнти є статистично незначущі. Для коефіцієнта
розрахункове значення статистики менше теоретичного, тому гіпотезу про рівність їх нулю відкинути не можна і ці коефіцієнти є статистично незначущі. Для коефіцієнта 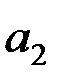
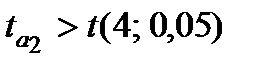 , тому статистична значущість коефіцієнта
, тому статистична значущість коефіцієнта 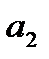 підтверджується.
підтверджується.
Отримані результати означають, що друга незалежна компонента (основний капітал) істотно впливає на залежну змінну (прибуток). Статистична незначущість коефіцієнта 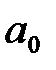 вказує на те, що всі інші фактори, не враховані в регресійній моделі, не роблять значного впливу на залежну змінну. Також фактор інвестиційних вкладень в оборотні кошти не впливає сильно на результат – прибуток.
вказує на те, що всі інші фактори, не враховані в регресійній моделі, не роблять значного впливу на залежну змінну. Також фактор інвестиційних вкладень в оборотні кошти не впливає сильно на результат – прибуток.
3. Визначення точності моделі
Для характеристики точності розрахуємо середню відносну похибку апроксимації (див. табл. 10): 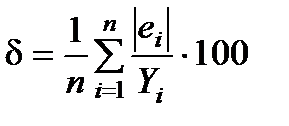 =7,74%. Ця величина не перевищує 10%, тому можна вважати точність моделі досить високою.
=7,74%. Ця величина не перевищує 10%, тому можна вважати точність моделі досить високою.
4. Аналіз впливу факторних змінних на результативний показник
1. Розрахуємо коефіцієнти еластичності:
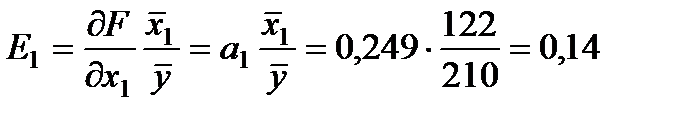 ;
; 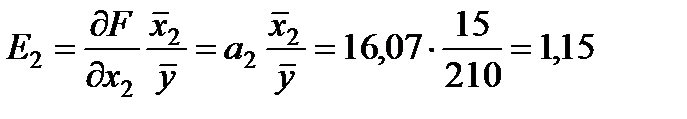 .
.
Це означає, що за збільшення внесків в оборотні кошти на 1% (фактор X1) і незмінної величини внесків в основний капітал прибуток зросте на 0,14%. У випадку збільшення внесків в основний капітал (фактор X2) на 1% прибуток зросте на 1,15%. Таким чином, інвестиційні вкладення в основний капітал більш значущі для виробництва.
2. Розрахуємо b-коефіцієнти. Для цього знайдемо середньоквадратичні відхилення для факторних змінних та результативного показника:
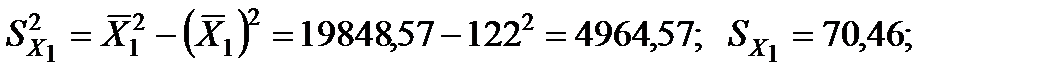
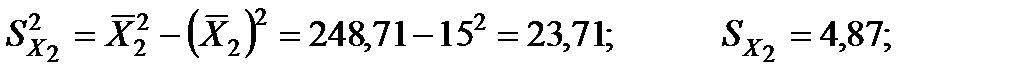
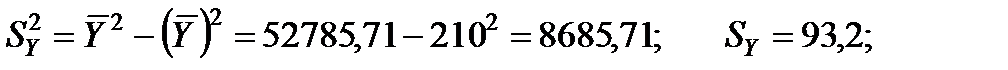
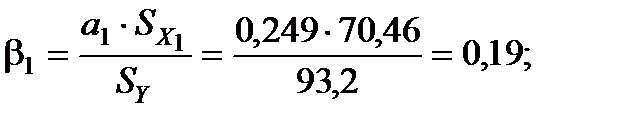
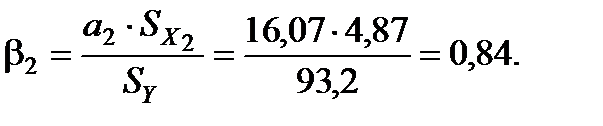
Отримані коефіцієнти показують, на яку частину величини середньоквадратичного відхилення зміниться в середньому значення залежної змінної у випадку зміни факторної ознаки на величину її середньоквадратичного відхилення.
3. Розрахуємо  -коефіцієнти:
-коефіцієнти: 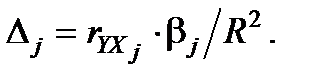 Для цього знайдемо коефіцієнти парної кореляції:
Для цього знайдемо коефіцієнти парної кореляції:
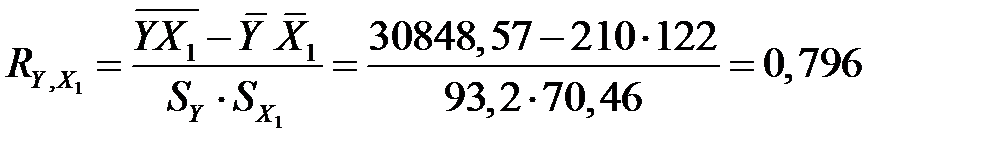 ;
;
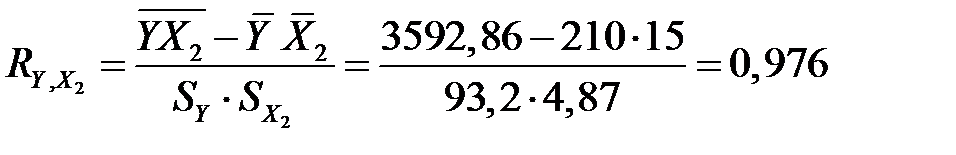 .
.
Тоді 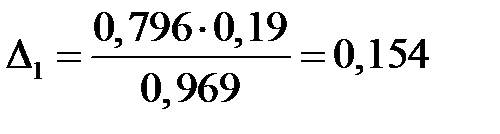 ;
; 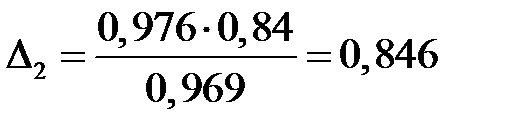 .
.
Це означає, що на 84,6% прирости прибутку підприємств можна пояснити вкладеннями в основний капітал і тільки на 15,4% – додатковими вкладеннями в оборотні кошти.
Прогнозування за економетричною моделлю
Розрахуємо для побудованої економетричної моделі точковий та інтервальний прогнози математичного сподівання й індивідуального значення залежної змінної, якщо для прогнозного періоду задано вектор значень незалежних факторів 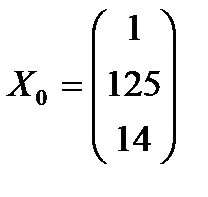 . Побудована модель має вигляд
. Побудована модель має вигляд
Y = –61,36+0,25x1+16,07x2.
Визначимо точкові прогнозні значення залежної змінної:
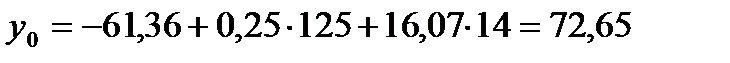 .
.
Величину y0 можна інтерпретувати як точкову оцінку прогнозного значення математичного сподівання та індивідуального значення приросту прибутку (Y), коли розмір інвестиційних вкладень в оборотні кошти дорівнює 125 тис. грн. (X1), а основний капітал – 14 тис. грн (X2).
Визначимо прогнозний інтервал для умовного середнього:
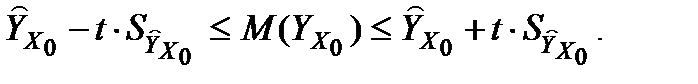
Дисперсія прогнозу умовного середнього складає
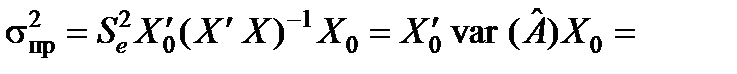
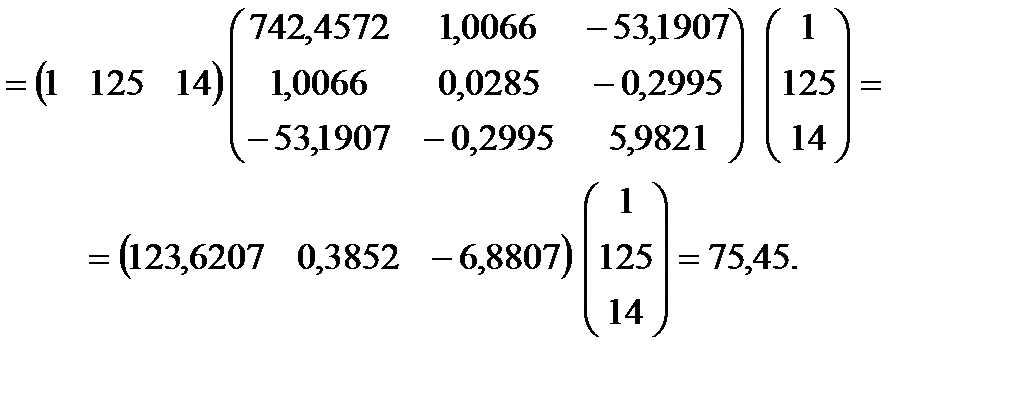
Стандартна похибка прогнозу математичного сподівання 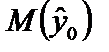 становить
становить
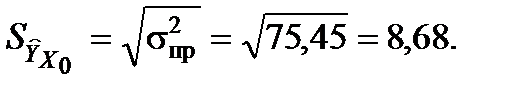
Значення t знайдемо з таблиці за a = 0,05 і степенями вільності n–k–1= 4. У такому разі t = 2,7764.
Тепер довірчий інтервал для 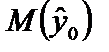 складає
складає
72, 65 – 2,7764 × 8,68 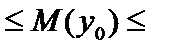 72, 65 + 2,7764 × 8,68;
72, 65 + 2,7764 × 8,68;
48,54 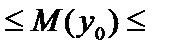 96,77.
96,77.
Знайдемо аналогічний довірчий інтервал для індивідуальних значень залежної змінної:
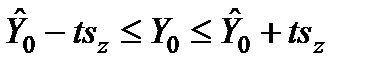 ,
,
де 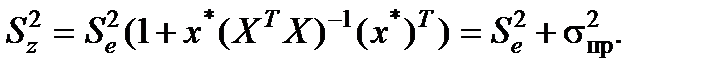
Обчислимо дисперсію і стандартну похибку прогнозу індивідуального значення 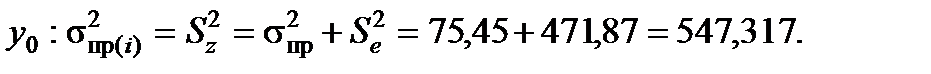
Стандартна похибка прогнозу індивідуального значення y0 така:
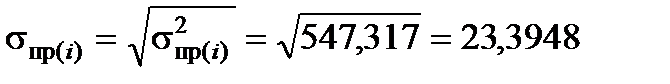 .
.
Визначимо інтервальний прогноз індивідуального значення y0:
72, 65 – 2,7764 × 23,3948 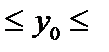 72, 65+ 2,7764 × 23,3948;
72, 65+ 2,7764 × 23,3948;
7,7021 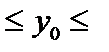 137,6108.
137,6108.
Економічна інтерпретація прогнозу така: якщо в прогнозному періоді розмір інвестиційних вкладень в оборотні кошти дорівнює 125 тис. грн (X1) і основний капітал складає 14 тис. грн (X2), то середня величина змін величини прибутку потрапляє в інтервал
48,54 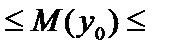 96,77.
96,77.
Водночас окреме (індивідуальне) значення цих змін величини прибутку міститиметься в ширшому інтервалі:
7,7021 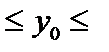 137,6108.
137,6108.
З імовірністю 0,95 (a = 0,05) знайдені інтервали покривають М(y0) і y0, якщо взяти досить велику кількість вибірок і для кожної з них обчислити прогнозні значення.
Завдання для самостійної роботи
За даними свого варіанта виконати такі завдання економетричного моделювання:
1) оцінити параметри моделі за допомогою МНК;
2) провести верифікацію моделі:
· перевірити виконання умов Гаусса – Маркова, зробити висновки;
· здійснити перевірку загальної якості рівняння регресії;
· розрахувати коефіцієнт детермінації, скорегований коефіцієнт детермінації, застосувати критерій Фішера;
· перевірити статистичну значущість коефіцієнтів рівняння регресії;
· визначити стандартні похибки і довірчі інтервали оцінок параметрів моделі, виконати перевірку точності моделі;
3) провести економічний аналіз економетричної моделі:
· розрахувати коефіцієнти еластичності, бета-коефіцієнти і дельта-коефіцієнти, дати пояснення;
· оцінити прогнозне значення залежної змінної за умови, що пояснювальні змінні задано на перспективу; отримати точковий та інтервальний прогнози, дати економічну інтерпретацію.
| Варіант 1 | Варіант 2 | ||||||||||
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т |
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т | |||
| 1 | 300 | 25 | 5 |
| 1 | 350 | 26 | 5 | |||
| 2 | 280 | 20 | 4 |
| 2 | 280 | 22 | 4 | |||
| 3 | 350 | 30 | 6 |
| 3 | 350 | 30 | 6 | |||
| 4 | 340 | 30 | 7 |
| 4 | 340 | 30 | 7 | |||
| 5 | 330 | 28 | 7 |
| 5 | 300 | 29 | 7 | |||
| 6 | 320 | 28 | 5 |
| 6 | 320 | 28 | 5 | |||
| 7 | 310 | 25 | 6 |
| 7 | 320 | 25 | 6 | |||
| 8 | 300 | 24 | 4 |
| 8 | 280 | 24 | 4 | |||
| 9 | 320 | 27 | 5 |
| 9 | 300 | 23 | 6 | |||
| 10 | 280 | 22 | 4 |
| 10 | 380 | 21 | 5 | |||
| 11 | 340 | 35 | 6 |
| 11 | 340 | 30 | 6 | |||
| 12 | 360 | 30 | 7 |
| 12 | 360 | 32 | 7 | |||
| 13 | 320 | 29 | 7 |
| 13 | 330 | 28 | 8 | |||
| 14 | 300 | 28 | 5 |
| 14 | 320 | 29 | 5 | |||
| 15 | 310 | 25 | 6 |
| 15 | 340 | 25 | 6 | |||
| 16 | 350 | 26 | 4 |
| 16 | 300 | 24 | 9 | |||
Варіант 3 | Варіант 4 | ||||||||||
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т |
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т | |||
| 1 | 400 | 25 | 5 |
| 1 | 320 | 15 | 5 | |||
| 2 | 380 | 20 | 4 |
| 2 | 280 | 10 | 4 | |||
| 3 | 350 | 30 | 6 |
| 3 | 350 | 20 | 6 | |||
| 4 | 360 | 30 | 7 |
| 4 | 340 | 20 | 7 | |||
| 5 | 430 | 28 | 7 |
| 5 | 330 | 18 | 7 | |||
| 6 | 420 | 28 | 5 |
| 6 | 320 | 18 | 5 | |||
| 7 | 310 | 25 | 6 |
| 7 | 310 | 15 | 6 | |||
| 8 | 400 | 24 | 4 |
| 8 | 300 | 14 | 4 | |||
| 9 | 350 | 25 | 5 |
| 9 | 310 | 15 | 5 | |||
| 10 | 380 | 20 | 4 |
| 10 | 290 | 10 | 4 | |||
| 11 | 350 | 30 | 6 |
| 11 | 350 | 20 | 6 | |||
| 12 | 340 | 30 | 7 |
| 12 | 340 | 20 | 7 | |||
| 13 | 320 | 28 | 7 |
| 330 | 18 | 7 | ||||
| 14 | 320 | 28 | 5 |
| 14 | 320 | 18 | 5 | |||
| 15 | 310 | 25 | 6 |
| 15 | 310 | 15 | 6 | |||
| 16 | 380 | 24 | 4 |
| 16 | 300 | 14 | 4 | |||
| Варіант 5 | Варіант 6 | ||||||||||
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т |
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т | |||
| 1 | 300 | 25 | 5 |
| 1 | 200 | 15 | 5 | |||
| 2 | 280 | 20 | 4 |
| 2 | 180 | 20 | 4 | |||
| 3 | 350 | 20 | 6 |
| 3 | 250 | 30 | 6 | |||
| 4 | 340 | 10 | 7 |
| 4 | 240 | 30 | 7 | |||
| 5 | 380 | 28 | 7 |
| 5 | 230 | 38 | 7 | |||
| 6 | 320 | 28 | 5 |
| 6 | 220 | 38 | 5 | |||
| 7 | 310 | 15 | 6 |
| 7 | 210 | 25 | 6 | |||
| 8 | 400 | 24 | 4 |
| 8 | 250 | 34 | 4 | |||
| 9 | 350 | 25 | 5 |
| 9 | 200 | 15 | 5 | |||
| 10 | 280 | 20 | 4 |
| 10 | 190 | 25 | 4 | |||
| 11 | 350 | 20 | 6 |
| 11 | 250 | 30 | 6 | |||
| 12 | 340 | 20 | 7 |
| 12 | 240 | 30 | 7 | |||
| 13 | 380 | 28 | 7 |
| 13 | 230 | 18 | 7 | |||
| 14 | 320 | 28 | 5 |
| 14 | 280 | 28 | 5 | |||
| 15 | 310 | 15 | 6 |
| 15 | 210 | 25 | 6 | |||
| 16 | 320 | 14 | 4 |
| 16 | 200 | 14 | 4 | |||
Варіант 7 | Варіант 8 | ||||||||||
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т |
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т | |||
| 1 | 100 | 30 | 90 |
| 1 | 200 | 30 | 80 | |||
| 2 | 120 | 35 | 75 |
| 2 | 220 | 35 | 75 | |||
| 3 | 130 | 40 | 85 |
| 3 | 230 | 40 | 85 | |||
| 4 | 125 | 30 | 90 |
| 4 | 225 | 35 | 90 | |||
| 5 | 140 | 45 | 105 |
| 5 | 240 | 45 | 95 | |||
| 6 | 150 | 30 | 93 |
| 6 | 250 | 50 | 93 | |||
| 7 | 155 | 55 | 97 |
| 7 | 255 | 55 | 97 | |||
| 8 | 160 | 60 | 100 |
| 8 | 260 | 62 | 100 | |||
| 9 | 100 | 30 | 80 |
| 9 | 200 | 30 | 80 | |||
| 10 | 120 | 35 | 75 |
| 10 | 220 | 38 | 75 | |||
| 11 | 130 | 40 | 85 |
| 11 | 230 | 40 | 85 | |||
| 12 | 125 | 30 | 100 |
| 12 | 225 | 36 | 90 | |||
| 13 | 140 | 45 | 95 |
| 13 | 240 | 45 | 95 | |||
| 14 | 150 | 50 | 93 |
| 14 | 250 | 50 | 93 | |||
| 15 | 155 | 55 | 97 |
| 15 | 255 | 55 | 97 | |||
| 16 | 160 | 60 | 100 |
| 16 | 260 | 60 | 98 | |||
Варіант 9 | Варіант 10 | ||||||||||
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т |
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т | |||
| 1 | 110 | 20 | 20 |
| 1 | 100 | 30 | 8 | |||
| 2 | 130 | 25 | 95 |
| 2 | 120 | 35 | 17 | |||
| 3 | 140 | 30 | 85 |
| 3 | 130 | 40 | 18 | |||
| 4 | 125 | 20 | 100 |
| 4 | 125 | 30 | 19 | |||
| 5 | 140 | 35 | 95 |
| 5 | 140 | 45 | 19 | |||
| 6 | 160 | 20 | 103 |
| 6 | 150 | 50 | 19 | |||
| 7 | 155 | 45 | 97 |
| 7 | 155 | 55 | 19 | |||
| 8 | 180 | 50 | 100 |
| 8 | 160 | 60 | 20 | |||
| 9 | 120 | 20 | 90 |
| 9 | 100 | 30 | 9 | |||
| 10 | 120 | 25 | 85 |
| 10 | 120 | 35 | 7 | |||
| 11 | 130 | 30 | 85 |
| 11 | 130 | 40 | 28 | |||
| 12 | 135 | 20 | 90 |
| 12 | 125 | 30 | 29 | |||
| 13 | 145 | 35 | 105 |
| 13 | 140 | 45 | 9 | |||
| 14 | 150 | 20 | 193 |
| 14 | 150 | 50 | 9 | |||
| 15 | 155 | 45 | 97 |
| 15 | 160 | 55 | 15 | |||
| 16 | 165 | 50 | 100 |
| 16 | 170 | 64 | 14 | |||
|
Варіант 11 |
Варіант 12 | ||||||||||
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т |
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т | |||
| 1 | 50 | 10 | 60 |
| 1 | 50 | 10 | 60 | |||
| 2 | 45 | 12 | 62 |
| 2 | 45 | 12 | 62 | |||
| 3 | 55 | 9 | 65 |
| 3 | 55 | 9 | 62 | |||
| 4 | 50 | 10 | 60 |
| 4 | 50 | 10 | 60 | |||
| 5 | 60 | 8 | 55 |
| 5 | 60 | 8 | 55 | |||
| 6 | 70 | 16 | 50 |
| 6 | 70 | 6 | 50 | |||
| 7 | 52 | 10 | 70 |
| 7 | 55 | 5 | 20 | |||
| 8 | 47 | 12 | 62 |
| 8 | 57 | 6 | 22 | |||
| 9 | 55 | 9 | 62 |
| 9 | 56 | 7 | 20 | |||
| 10 | 50 | 10 | 60 |
| 10 | 59 | 8 | 25 | |||
| 11 | 65 | 18 | 85 |
| 11 | 51 | 9 | 20 | |||
| 12 | 70 | 9 | 50 |
| 12 | 58 | 10 | 15 | |||
| 13 | 68 | 12 | 62 |
| 13 | 57 | 11 | 23 | |||
| 14 | 72 | 15 | 81 |
| 14 | 55 | 9 | 22 | |||
| 15 | 75 | 11 | 53 |
| 15 | 57 | 12 | 19 | |||
| Варіант 13 | Варіант 14 | ||||||||||
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т |
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т | |||
| 1 | 50 | 10 | 70 |
| 1 | 50 | 10 | 90 | |||
| 2 | 45 | 12 | 62 |
| 2 | 45 | 12 | 62 | |||
| 3 | 55 | 9 | 72 |
| 3 | 55 | 19 | 82 | |||
| 4 | 50 | 10 | 60 |
| 4 | 50 | 10 | 60 | |||
| 5 | 60 | 18 | 55 |
| 5 | 60 | 8 | 85 | |||
| 6 | 70 | 6 | 60 |
| 6 | 70 | 16 | 50 | |||
| 7 | 50 | 15 | 60 |
| 7 | 50 | 10 | 70 | |||
| 8 | 45 | 12 | 82 |
| 8 | 45 | 12 | 62 | |||
| 9 | 55 | 19 | 62 |
| 9 | 55 | 9 | 62 | |||
| 10 | 50 | 10 | 60 |
| 10 | 50 | 10 | 80 | |||
| 11 | 60 | 9 | 85 |
| 11 | 60 | 12 | 65 | |||
| 12 | 70 | 14 | 60 |
| 12 | 70 | 14 | 60 | |||
| 13 | 65 | 17 | 67 |
| 13 | 55 | 19 | 67 | |||
| 14 | 58 | 13 | 70 |
| 14 | 59 | 13 | 70 | |||
| 15 | 62 | 16 | 81 |
| 15 | 64 | 16 | 75 | |||
| 16 | 71 | 18 | 76 |
| 16 | 71 | 14 | 76 | |||
| Варіант 15 | Варіант 16 | ||||||||||
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т |
| Номер складу | Затрати на реалізацію продукції, млн грн | Обсяг товаро-обігу, млн т | Середній рівень товарних запасів, млн т | |||
| 1 | 50 | 10 | 70 |
| 1 | 55 | 5 | 100 | |||
| 2 | 45 | 12 | 62 |
| 2 | 57 | 6 | 110 | |||
| 3 | 55 | 9 | 62 |
| 3 | 56 | 7 | 112 | |||
| 4 | 50 | 10 | 60 |
| 4 | 59 | 8 | 115 | |||
| 5 | 60 | 8 | 55 |
| 5 | 51 | 9 | 120 | |||
| 6 | 70 | 6 | 50 |
| 6 | 58 | 10 | 135 | |||
| 7 | 80 | 8 | 82 |
| 7 | 60 | 8 | 140 | |||
| 8 | 85 | 10 | 65 |
| 8 | 50 | 9 | 120 | |||
| 9 | 75 | 12 | 74 |
| 9 | 45 | 15 | 110 | |||
| 10 | 90 | 7 | 87 |
| 10 | 65 | 8 | 130 | |||
| 11 | 45 | 15 | 62 |
| 11 | 70 | 11 | 150 | |||
| 12 | 50 | 14 | 60 |
| 12 | 52 | 12 | 170 | |||
| 13 | 85 | 15 | 84 |
| 13 | 65 | 14 | 120 | |||
| 14 | 70 | 17 | 77 |
| 14 | 55 | 13 | 140 | |||
| 15 | 65 | 16 | 82 |
| 15 | 71 | 11 | 160 | |||
| 16 | 80 | 14 | 70 |
| 16 | 62 | 14 | 165 | |||
Контрольні запитання й завдання
1. Дайте визначення загальної економетричної моделі.
2. Назвіть етапи побудови економетричної моделі.
3. Чому необхідно часто будувати модель множинної регресії? Наведіть приклади економічних процесів і явищ, щодо яких ви б застосували цю модель?
4. У чому полягає відмінність цілей побудови моделі парної регресії і моделі множинної регресії?
5. У чому ви вбачаєте характерні особливості специфікації моделі множинної регресії?
6. Яким вимогам повинні відповідати чинники моделі множинної регресії і чому?
7. Яка сутність специфікації моделі?
8. Коли для оцінювання параметрів моделі можна застосовувати МНК?
9. Запишіть оператор оцінювання МНК. Як його можна одержати?
10. Які властивості повинні мати оцінки параметрів економетричної моделі?
11. Як визначити зміщення оцінки МНК?
12. Як обчислити матрицю коваріацій параметрів моделі?
13. Запишіть формулу визначення дисперсії залишків.
14. Як визначити дисперсію залишків, загальну дисперсію і дисперсію регресії? Який між ними зв’язок?
15. Як визначають F-критерій? Для чого його застосовують?
16. Покажіть залежність між F-критерієм і R2.
17. Як оцінити достовірність коефіцієнта кореляції?
18. Як обчислюють t-критерій?
19. Що називають стандартною похибкою оцінок параметрів моделі? Наведіть альтернативні формули для її обчислення.
20. Як визначити довірчі інтервали для параметрів моделі?
21. Як повинні співвідноситися коефіцієнти детермінації для m і m+1 чинників моделі?
22. Поясніть практичне застосування в економіці частинних коефіцієнтів еластичності, бета-коефіцієнтів, дельта-коефіцієнтів.
Додатки
Додаток 1