Оцінка точності моделі
Аналогічно до випадку парної регресії для оцінки точності можна розглядати величину відносної похибки апроксимації в i -му спостереженні:
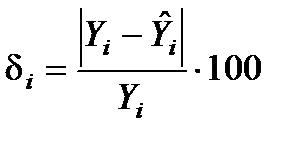 ,
, 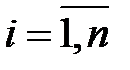 .
.
Для судження про точність моделі визначають середню відносну похибку апроксимації:
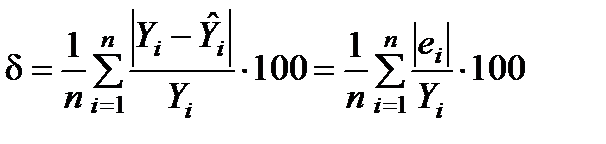 .
.
Похибка, менша 7–10%, свідчить про якісний підбір моделі до початкових даних (висока точність). У разі похибки, більшої 15%, слід вибрати інший тип рівняння моделі.
Змістова перевірка якості економетричної моделі
Нагадаємо, що під змістовим складником аналізу якості розуміють розгляд економічного змісту отриманої моделі і її коефіцієнтів. Для економічної інтерпретації зв'язків між факторними змінними і залежною змінною зазвичай застосовують коефіцієнти еластичності, бета-коефіцієнти і дельта-коефіцієнти. Розглянемо їх окремо.
Коефіцієнти еластичності характеризують відносну зміну залежної змінної за зміни пояснювальної змінної на 1%. Якщо рівняння моделі 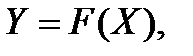 то коефіцієнти еластичності розраховують таким чином:
то коефіцієнти еластичності розраховують таким чином: 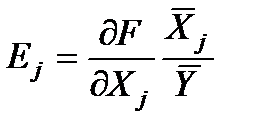 , де
, де 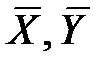 – середні величини, а похідна взята в точці
– середні величини, а похідна взята в точці 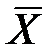 .
.
Бета-коефіцієнти ( 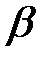 -коефіцієнти), або коефіцієнти регресії, у стандартизованому вигляді застосовують для усунення відмінностей у розмірності чинників. Обчислюють їх за формулою
-коефіцієнти), або коефіцієнти регресії, у стандартизованому вигляді застосовують для усунення відмінностей у розмірності чинників. Обчислюють їх за формулою
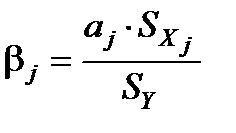 ,
,
де 
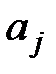 – коефіцієнт перед змінною
– коефіцієнт перед змінною 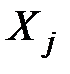 в рівнянні регресії;
в рівнянні регресії;
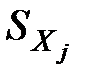 =
= 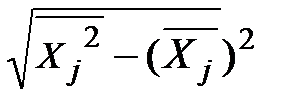 – стандартна похибка у визначенні змінної
– стандартна похибка у визначенні змінної 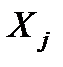 ;
;
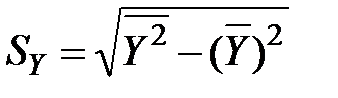 – стандартна похибка у визначенні змінної Y.
– стандартна похибка у визначенні змінної Y.
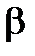 -Коефіцієнт показує, на яку частину величини середньоквадратичного відхилення зміниться в середньому значення залежної змінної Y у випадку зміни факторної ознаки
-Коефіцієнт показує, на яку частину величини середньоквадратичного відхилення зміниться в середньому значення залежної змінної Y у випадку зміни факторної ознаки 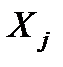 на величину її середньоквадратичного відхилення.
на величину її середньоквадратичного відхилення.
Дельта-коефіцієнт (  -коефіцієнт) характеризує внесок кожного чинника в сумарний вплив на результуючий показник (за умови незалежності чинників). Його обчислюють так:
-коефіцієнт) характеризує внесок кожного чинника в сумарний вплив на результуючий показник (за умови незалежності чинників). Його обчислюють так:
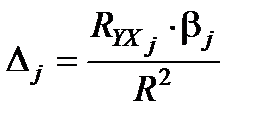 ,
,
де R2 – коефіцієнт детермінації; 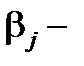 відповідний бета-коефіцієнт;
відповідний бета-коефіцієнт; 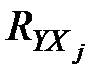 – коефіцієнт парної кореляції між j-м фактором
– коефіцієнт парної кореляції між j-м фактором 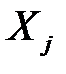 і залежною змінною Y:
і залежною змінною Y:
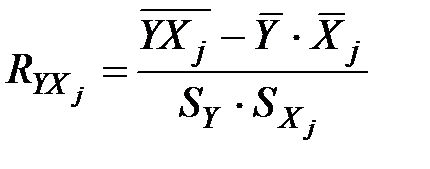 .
.
Зауваження.
1. Доведено, що 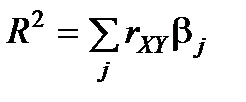 , тому
, тому 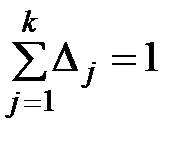 .
.
2. У випадку коректного аналізу, величини 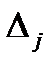 додатні. Тобто всі коефіцієнти регресії мають той же знак, що й відповідні парні коефіцієнти кореляції. Проте в разі сильної корельованості пояснювальних змінних деякі дельта-коефіцієнти можуть бути від’ємними через те, що відповідний коефіцієнт регресії має знак, протилежний до парного коефіцієнта кореляції.
додатні. Тобто всі коефіцієнти регресії мають той же знак, що й відповідні парні коефіцієнти кореляції. Проте в разі сильної корельованості пояснювальних змінних деякі дельта-коефіцієнти можуть бути від’ємними через те, що відповідний коефіцієнт регресії має знак, протилежний до парного коефіцієнта кореляції.
Прогнозування за допомогою економетричних моделей
Одне з важливих завдань економетричного моделювання – оцінити прогнозне значення залежної змінної за умови, що пояснювальні змінні задані на перспективу. На основі економетричної моделі можна отримати точковий та інтервальний прогнози залежної змінної на перспективу.
Для отримання точкового прогнозу підставляють досліджуване значення 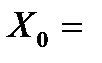
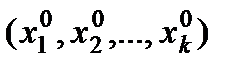 у рівняння моделі та знаходять
у рівняння моделі та знаходять 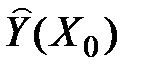 =
= 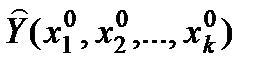 – точкову оцінку, або точковий прогноз.
– точкову оцінку, або точковий прогноз.
Оскільки параметри моделі 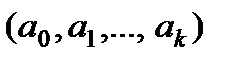 містять випадкові похибки, то залежна змінна
містять випадкові похибки, то залежна змінна 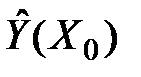 , знайдена за рівнянням моделі в деякій точці
, знайдена за рівнянням моделі в деякій точці 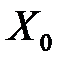 , є випадковою величиною і, отже, визначає деяке умовне середнє значення Y в точці
, є випадковою величиною і, отже, визначає деяке умовне середнє значення Y в точці 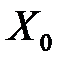 . Імовірність потрапляння Y в знайдену точку
. Імовірність потрапляння Y в знайдену точку 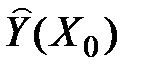 практично дорівнює нулю, тому стають необхідними перспективні оцінки у вигляді «вилки» значень через довірчі інтервали – інтервальний прогноз.
практично дорівнює нулю, тому стають необхідними перспективні оцінки у вигляді «вилки» значень через довірчі інтервали – інтервальний прогноз.
Довірчі інтервали будують за припущення, що факторні змінні набули значень, задаваних вектором 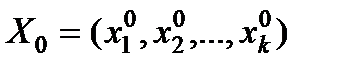 .
.
Довірчий інтервал для умовного середнього визначають, як і в разі парної регресії, за формулою
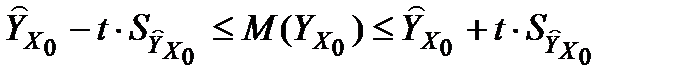 ,
,
причому 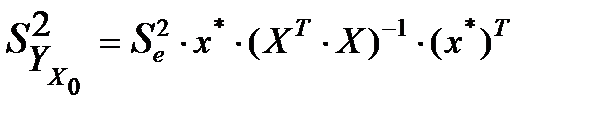 , де
, де 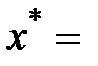
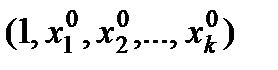 .
.
Аналогічний довірчий інтервал для індивідуальних значень залежної змінної набуде вигляду
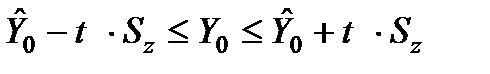 ,
,
де 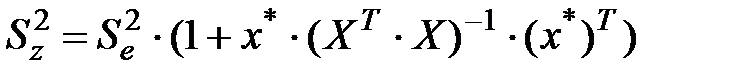 .
.
Нагадаємо такі властивості довірчих інтервалів для прогнозів:
· довірчий інтервал для індивідуального значення Y0 ширший, ніж довірчий інтервал для середнього значення E(Y|X0) за тих же умов;
· ширина довірчих областей найменша у випадку 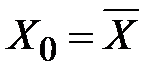 (середнє значення за вибіркою) та збільшується в міру віддалення Х0 від
(середнє значення за вибіркою) та збільшується в міру віддалення Х0 від 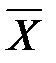 . Така поведінка свідчить про те, що якщо
. Така поведінка свідчить про те, що якщо 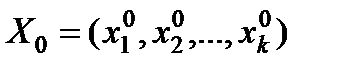 сильно відрізняється від середнього, ширина довірчого інтервалу істотно збільшується, а це свідчить про розпливчатість прогнозу;
сильно відрізняється від середнього, ширина довірчого інтервалу істотно збільшується, а це свідчить про розпливчатість прогнозу;
· досліджуване значення 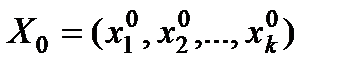 може лежати як усередині вибірки, так і поза нею. Водночас, коли Х0 виходить за межі вибірки й знаходиться на значній відстані від
може лежати як усередині вибірки, так і поза нею. Водночас, коли Х0 виходить за межі вибірки й знаходиться на значній відстані від 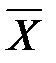 , потрібно дуже обережно екстраполювати регресію для прогнозу.
, потрібно дуже обережно екстраполювати регресію для прогнозу.
Зауваження.
1. Значення факторних змінних, що утворюють досліджуваний вектор (матрицю) 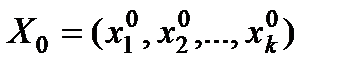 можна отримати як експертні оцінки або прогнозуванням відповідних часових рядів.
можна отримати як експертні оцінки або прогнозуванням відповідних часових рядів.
2. Отримані на основі прогнозу дані слід критично осмислити з розгляду змісту.
Обернена задача прогнозування
У дещо іншій формі проблему прогнозування можна сформулювати так: у разі одержання нової пари спостережень 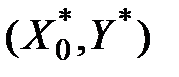 необхідно з'ясувати, чи задовольняє вона попередню залежність, тобто чи дорівнює
необхідно з'ясувати, чи задовольняє вона попередню залежність, тобто чи дорівнює 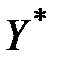 значенню
значенню 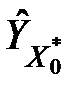 , отриманому підстановкою
, отриманому підстановкою 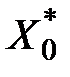 в рівняння моделі.
в рівняння моделі.
Алгоритм розв’язування оберненої задачі
Крок 1. Розглянемо величину 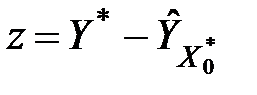 . Сформулюємо дві гіпотези:
. Сформулюємо дві гіпотези:
· H0 : 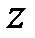 = 0, тобто значення
= 0, тобто значення 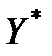 та
та 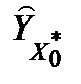 збігаються;
збігаються;
· H1 : 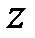 ≠ 0, значення
≠ 0, значення 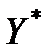 та
та 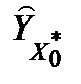 не збігаються.
не збігаються.
Крок 2. Величина 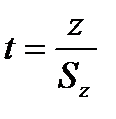 має розподіл Стьюдента з
має розподіл Стьюдента з 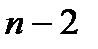 степенями вільності. Оцінку дисперсії величини z обчислимо за формулою
степенями вільності. Оцінку дисперсії величини z обчислимо за формулою
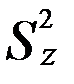 =
= 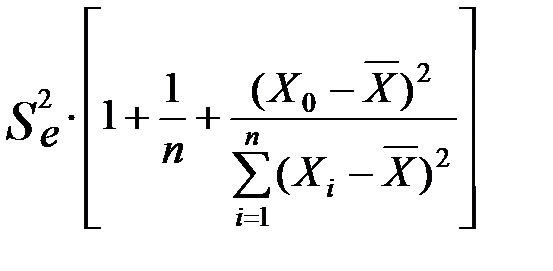 .
.
Крок 3. Застосуємо правило прийняття рішень:
· якщо розрахункове значення t-статистики менше табличного за модулем, то нульову гіпотезу слід прийняти, тобто з вибраним рівнем довіри можна стверджувати, що значення 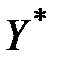 не відрізняється від значення
не відрізняється від значення 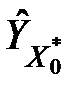 , знайденого за рівнянням моделі, і пара
, знайденого за рівнянням моделі, і пара 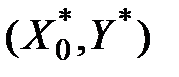 відповідає даній залежності;
відповідає даній залежності;
· якщо розрахункове значення t-статистики більше табличного, то нульову гіпотезу треба відкинути, тобто з вибраним рівнем довіри можна стверджувати, що значення 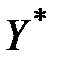 статистично значущо відрізняється від значення
статистично значущо відрізняється від значення 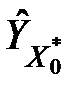 , знайденого за рівнянням моделі, і пара
, знайденого за рівнянням моделі, і пара 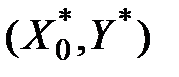 не відповідає даній залежності.
не відповідає даній залежності.
Приклад виконання розрахунків
Маємо статистичні дані про приріст прибутку (Y) за 7 підприємствами галузі залежно від інвестиційних вкладень в оборотні кошти (X1) і основний капітал (X2). Проаналізувати залежність приросту прибутку від цих показників, використовуючи початкові дані табл. 9.
Таблиця 9
| Y | 50 | 120 | 290 | 190 | 200 | 300 | 320 |
| X1 | 30 | 66 | 78 | 110 | 130 | 190 | 250 |
| X2 | 6 | 10 | 20 | 15 | 16 | 18 | 20 |
Етапи розв’язування








