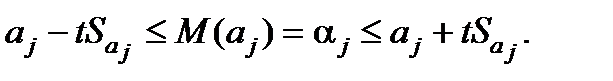Перевірка статистичної значущості коефіцієнтів рівняння регресії
Нагадаємо, що оскільки побудова економетричних моделей ґрунтується на вибіркових статистичних даних, то обчислені параметри відрізнятимуться від відповідних величин, розрахованих за генеральною сукупністю. Тому вибіркові характеристики потребують перевірки статистичної значущості. Крім оцінки значущості рівняння регресії в цілому проводять оцінку індивідуальної статистичної значущості кожного з коефіцієнтів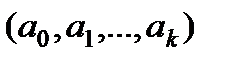 
.
Поняття дисперсійно-коваріаційної матриці параметрів
У класичній регресійній моделі Y = XA + е вектор збурень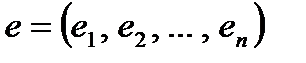 
і залежний вектор 
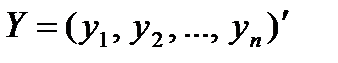є випадковими змінними. До оператора оцінювання 
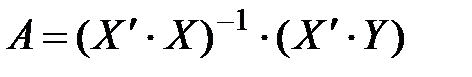входить вектор Y, а отже, оператор А також можна вважати випадковою функцією оцінювання параметрів моделі 
.
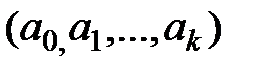Відомо, що для характеристики випадкових змінних поряд із математичним сподіванням застосовують дисперсію і коваріацію. Тому для визначення показників випадкового розсіювання оцінок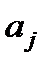 
навколо відповідних істинних значень параметрів 
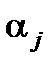, а також характеристик взаємозв’язків отриманих оцінок будують дисперсійно-коваріаційну матрицю.
Визначення. Дисперсійно-коваріаційна матриця істинних значень параметрів класичної економетричної моделі має вигляд
.
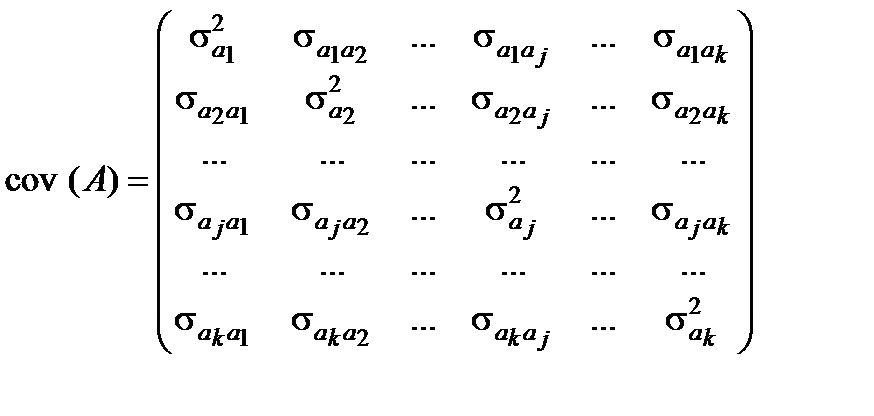На головній діагоналі матриці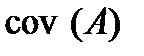 
містяться оцінки дисперсій параметрів, 
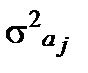, елементи поза головною діагоналлю є оцінками коваріації між відповідними параметрами 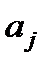і 
.
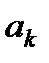Дисперсійно-коваріаційну матрицю параметрів обчислюють за формулою
,
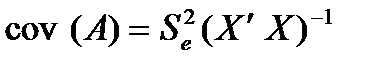де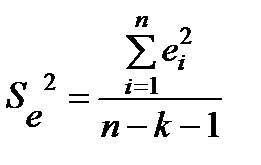 
– незміщена оцінка дисперсії залишків.
Оцінки коваріаційної матриці застосовують для знаходження стандартних похибок та обчислення довірчих інтервалів оцінок параметрів 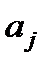. Їх застосовують і в процесі перевірки статистичної значущості останніх.
Оцінка статистичної значущості параметрів
Нехай параметри моделі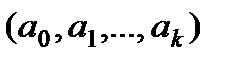 
, розраховані за даними вибірки, є випадковими величинами. Їх математичні сподівання у випадку виконання передумов про відхилення ei дорівнюють відповідно 
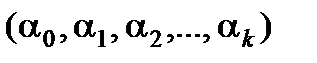. Виберемо для перевірки деякий параметр 
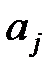. Далі виконаємо такі дії.
Крок 1. Сформулюємо дві гіпотези: H0: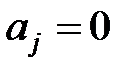 
і H1: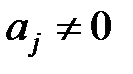 
.
Крок 2. Розрахуємо t-статистику: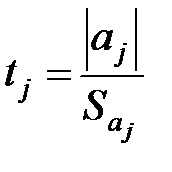 
.
Вибіркову дисперсію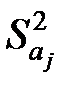 
параметра 
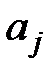обчислимо за формулою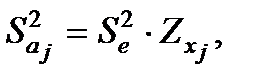 
де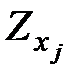 
– діагональний елемент матриці 
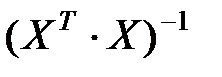, що відповідає змінній 
; 
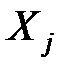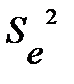– оцінка дисперсії залишків.
Крок 3. Порівняємо розрахункове значення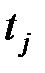 
з табличним значенням
t-статистики Стьюдента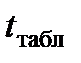 
.
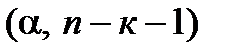Нагадаємо, що рівень статистичної значущості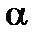 
є ймовірністю похибки, пов'язаної з поширенням спостережуваного результату на всю генеральну сукупність. Кількість степенів вільності n–k–1 – це кількість незалежних параметрів, необхідних для визначення характеристики.
Крок 4. Якщо розрахункове значення статистики більше табличного
( 
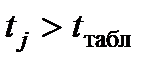), то відхилимо нульову гіпотезу і з вибраною ймовірністю стверджуватимемо, що коефіцієнт регресії 
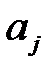статистично значущий (тобто в генеральній сукупності він відмінний від нуля з вибраною ймовірністю). Отже, факторна змінна 
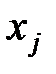істотно впливає на результативний показник.
Якщо параметр 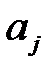статистично незначущий (статистично близький до нуля), це означає, що чинник 
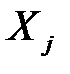не робить серйозного впливу на величину залежної змінної. У цьому випадку доцільно розглянути питання про виключення змінної 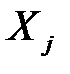з рівняння. Винятком є випадок, коли за незначущого коефіцієнта залежність між Xj і Y існує, але нелінійна. При цьому треба змінити специфікацію моделі (надати їй іншої аналітичної форми).
Для статистично значущих параметрів можна побудувати довірчий інтервал, що показує з імовірністю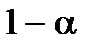 
можливий інтервал зміни істинних параметрів моделі 
:
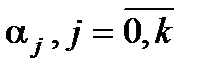