Перевірка статистичної значущості

Дата: 2025-06-02; Просмотры: 11
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Побудова економетричної моделі ґрунтується на вибіркових статистичних даних. Параметри рівняння, коефіцієнти кореляції й інші характеристики моделі, визначені на основі вибіркової сукупності спостережень, відрізняються від відповідних величин, розрахованих за генеральною сукупністю. Тому вибіркові характеристики містять помилки, пов'язані з неповним охопленням спостереженнями всіх одиниць генеральної сукупності. А отже, слід перевіряти надійність і статистичну значущість параметрів моделі й ті характеристики, за якими оцінюють її адекватність.

Статистична значущість результату є оцінена міра упевненості в його надійності. Для оцінки статистичної значущості вводять поняття рівня статистичної значущості та рівня надійності.

Визначення. Рівень значущості α – це ймовірність відхилення гіпотези за умови, що вона правильна, тобто α-рівень – імовірність помилки, пов'язаної з поширенням спостережуваного результату на всю генеральну сукупність. Наприклад, α = 0,05 показує, що є 5%-на ймовірність того, що знайдений у вибірці зв'язок між змінними є лише випадковою особливістю цієї вибірки.

Вибір певного рівня значущості, за перевищення якого результати відкидають як помилкові, є досить довільний. В економетричних дослідженнях рівень 0,05 є прийнятною межею статистичної значущості. Результати з рівнем, вищим 0,05 розглядають як високозначущі.

Визначення. Величину g = 1-a, обернену до рівня значущості a, називають надійністю результату.

Перевірка статистичної значущості передбачає перевірку статистичних гіпотез, яка включає такі етапи:

· формулювання завдання дослідження у вигляді основної статистичної гіпотези та вибір альтернативної гіпотези;

· вибір статистичного критерію та обчислення його фактичного значення;

· визначення критичної області, а також критичного значення статистичного критерію за відповідною таблицею теоретичних розподілів;

· перевірка основної гіпотези на основі порівняння фактичного і критичного значень критерію. Залежно від результатів перевірки основну гіпотезу або відхиляють, або приймають.

Зауваження. Перевірка якої-небудь характеристики моделі на статистичну значущість означає перевірку гіпотези про те, чи не може ця характеристика дорівнювати нулю в генеральній сукупності.

Перевірка гіпотез найпростішої двовимірної моделі регресії включає перевірку:

1) статистичної значущості коефіцієнта кореляції r;

2) статистичної значущості оцінок параметрів 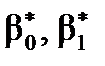економетричної моделі;

3) загальної значущості оціненої парної моделі регресії.

Розглянемо кожне питання окремо.

 

1. Перевірка статистичної значущості коефіцієнта кореляції

Для перевірки гіпотези Н0: r = 0 (коефіцієнт кореляції незначущий) і альтернативної їй гіпотези Н1: r ≠ 0 (коефіцієнт кореляції відмінний від нуля та значущий) підраховують статистичний критерій: .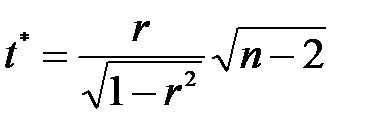

За заданим рівнем значущості a і степенями вільності 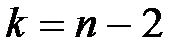встановлюють критичне значення 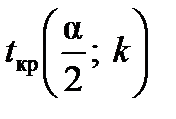(таблиця розподілу Стьюдента) та порівнюють обчислене значення 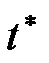з табличним. На основі порівняння роблять висновок стосовно прийняття гіпотези.

Правило прийняття рішення

1. Якщо 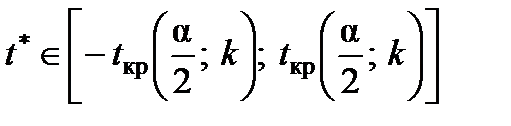, то приймають гіпотезу Н0 про статистичну незначущість розрахованого коефіцієнта кореляції.

2. Якщо 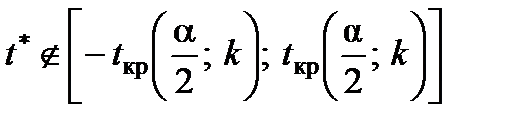, то приймають гіпотезу Н1 про статистичну значущість коефіцієнта кореляції.

2. Перевірка статистичної значущості оцінок параметрів 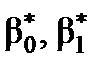економетричної моделі

Для перевірки нульової гіпотези 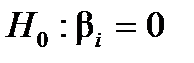(коефіцієнт незначущий) за альтернативної гіпотези 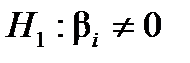(коефіцієнт значущий) вибирають як статистичний критерій випадкову величину 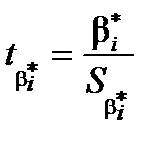( 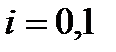), де 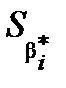– стандартні похибки оцінок параметрів (дод. 1).

Для розрахунку 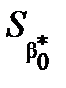та 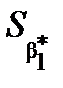застосовують формули

,

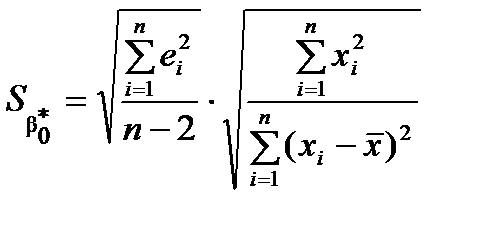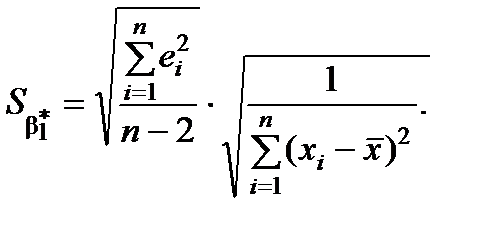
Далі знаходять критичне значення 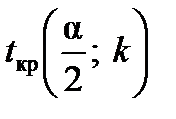з t-розподілу Стьюдента із 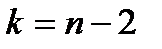степенями вільності за обраним рівнем значущості a.

Правило прийняття рішення

1. Якщо 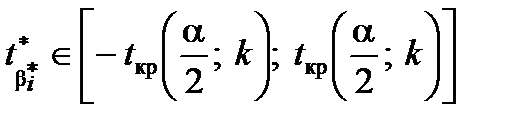, то приймають гіпотезу Н0 про те,
що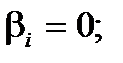

2. Якщо 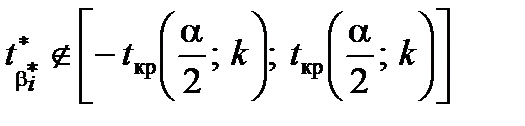, то приймають гіпотезу 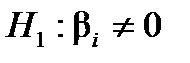про значущість вибіркового коефіцієнта регресії.

Зауваження.

1. Стандартні похибки характеризують середні лінійні коливання оцінок параметрів моделі навколо свого математичного сподівання. Чим менші ці похибки, тим більш стійкі оцінки параметрів.

2. Статистична значущість коефіцієнта 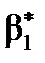свідчить про істотний вплив на залежну змінну вибраної незалежної та дозволяє визначити модель як якісну.

3. Статистична незначущість коефіцієнта 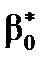вказує на те, що всі інші фактори, які не були враховані в регресійній моделі, не роблять значного впливу на залежну змінну.

Поняття довірчого інтервалу параметрів регресії

Розраховані значення показників є наближені, отримані на основі вибіркових даних. Для оцінки того, наскільки точні значення показників можуть відрізнятися від розрахованих, для статистично значущих параметрів можна побудувати довірчий інтервал.

Визначення. Довірчий інтервал – це інтервал, у якому з певною ймовірністю можна очікувати фактичне значення досліджуваної величини.

Довірчі інтервали коефіцієнтів 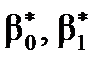обчислюють за формулами

- для : ;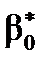

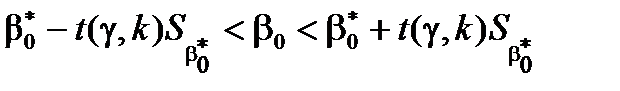- для : ,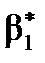

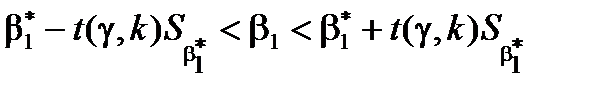де 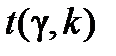визначають згідно з таблицею розподілу Стьюдента за заданою надійністю g = 1-a і кількістю степенів вільності .

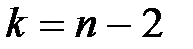3. Перевірка загальної значущості оціненої парної моделі регресії

Значущість усього рівняння в цілому оцінюють за допомогою F-критерію Фішера. Гіпотезу H0 про статистичну незначущість рівняння регресії (відсутність зв’язку між залежною і незалежною змінними) перевіряють порівнянням фактичного та критичного (табличного) значення F-критерію. Формула розрахунку фактичного F-критерію через коефіцієнт детермінації має вигляд

.

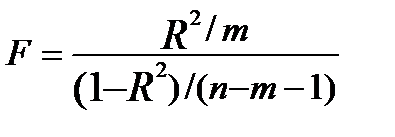Фактичне значення F-критерію порівнюють із табличним значенням
F-розподілу Фішера за степенів вільності n – m і m – 1 (для парної регресії m=1) і вибраного рівня довіри.

Правило прийняття рішення

1. Якщо Fфакт > Fтабл, то гіпотезу H0 відхиляють та підтверджують значущість зв’язку ж залежною і незалежною змінними економетричної моделі, при цьому модель вважають надійною.

2. Якщо Fфакт < Fтабл, то гіпотезу H0 не відхиляють і визнають статистичну незначущість та ненадійність рівняння регресії.

Зауваження. Для моделі лінійної парної регресії статистичну значущість рівняння можна перевірити на основі коефіцієнта парної кореляції .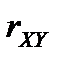
У цьому випадку 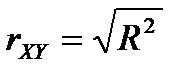. Перевірку проводять за стандартною схемою статистичної перевірки гіпотез із застосуванням t-статистики Стьюдента.

Розрахункове значення статистики складає 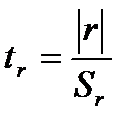. У цій формулі значення 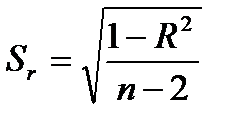(стандартну похибку у визначенні величини 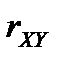) порівнюють із табличним 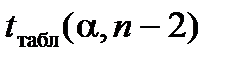. Якщ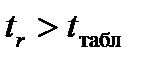о , то 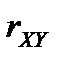з вибраним рівнем довіри визнають статистично значущим, а модель – адекватною і надійною.

Для коефіцієнта кореляції можна побудувати довірчий інтервал:

.

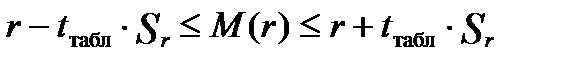Чим ширший інтервал, тим більша невизначеність в оцінці зв'язку 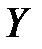та .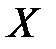

Перевірка точності моделі

Фактичні значення результативного показника відрізняються від теоретичних, розрахованих за рівнянням моделі, на величину 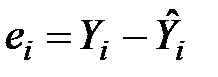. Ця величина в кожному спостереженні є похибкою апроксимації. Відхилення 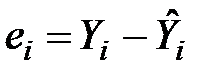становлять абсолютну похибку, але вони непорівнянні між собою, оскільки залежать від одиниць виміру і масштабу величин .

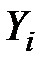Так, якщо в одному спостереженні вийшла похибка 5, а в іншому – 10, це не означає, що в останньому випадку модель дає гірший результат. Тому для того щоб оцінки були порівнянними, розглядають відношення відхилень до фактичних значень (у процентах). Оскільки 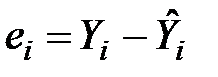може бути як додатною, так і від’ємною величиною, то відхилення беруть за модулем.

Визначення. Величину 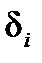= 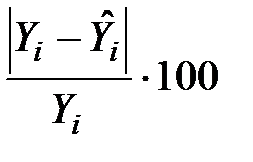, , 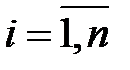називають відносною похибкою апроксимації в i-му спостереженні.

Щоб скласти загальне уявлення про точність моделі, визначають середню відносну похибку апроксимації:

.

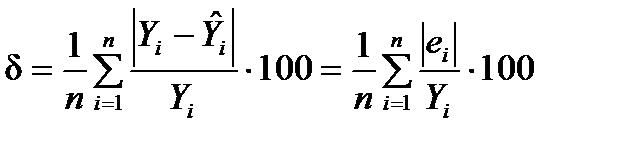Похибка, менша 7–10%, свідчить про хороший підбір моделі до початкових даних (висока точність). У разі похибки, більшої 15%, слід вибрати інший тип рівняння моделі. В економетричному аналізі застосовують й інші алгоритми для розрахунку точності моделі.

Застосування регресійного аналізу: проблема прогнозування

Побудоване на основі вибіркових даних рівняння регресії можна застосовувати для прогнозування, або передбачення, майбутніх значень Y, відповідних деякому заданому Х. Найбільш грубою оцінкою прогнозу буде визначення однієї точки 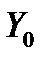для заданого значення 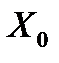– так званий точковий прогноз. Оскільки значення 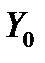є оцінкою, то, напевно, його числове значення відрізняється від істинного. Тому для розрахунку точних прогнозів визначають не одну точку, а прогнозний інтервал. Можливі такі два види прогнозу:

1) середній – прогноз умовної середньої величини Y, відповідний
вибраному Х0;

2) індивідуальний – прогноз індивідуальної величини Y, відповідної Х0.

Прогнозування середнього значення залежної змінної

Довірчий інтервал для теоретичної функції регресії знаходять за формулою

,

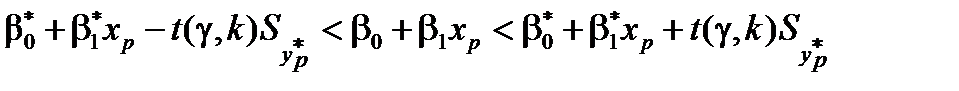де 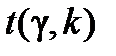визначають відповідно до таблиці розподілу Стьюдента за заданою надійністю g = 1-a і кількістю степенів вільності 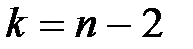, а 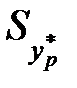обчислюють згідно з формулою

.

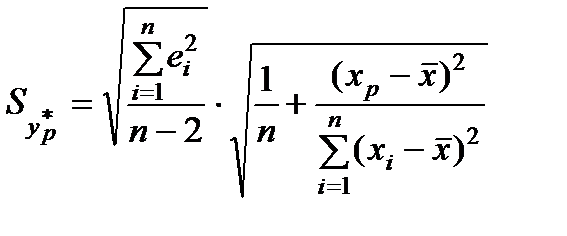Прогнозування індивідуального значення залежної змінної

Довірчий інтервал для прогнозованого індивідуального значення 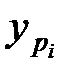із заданою надійністю g становить

,

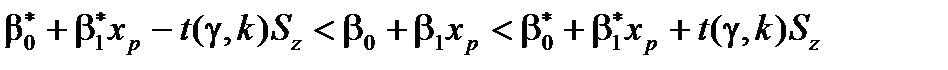де 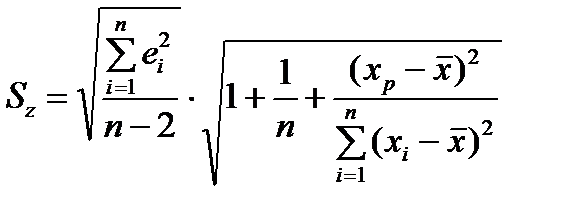, 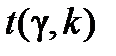визначають так, як описано вище.

Зауваження.

1. Ширина довірчого інтервалу прогнозу залежить від значення 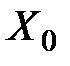: за 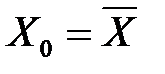вона мінімальна, а в міру віддалення 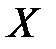від середнього значення ширина довірчого інтервалу збільшується (рис. 4).

Рис.4. Довірча область

для умовних середніх залежної змінної

2. Для індивідуальних значень змінної Y довірчий інтервал за того ж рівня довіри ширший, ніж для умовного середнього 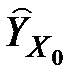, і включає довірчий інтервал для умовного середнього значення.