Аналіз якості рівняння регресії як математичної моделі
Для практичного застосування економетричної моделі велике значення має її адекватність, тобто відповідність реальному процесу і тим статистичним даним, на основі яких побудовано модель.
Аналіз якості (верифікація моделі) включає перевірку:
- загальної якості рівняння регресії;
- статистичної значущості коефіцієнтів;
- точності моделі;
- властивостей, виконання яких було передбачено в ході оцінювання рівняння, наприклад умов Гаусса – Маркова (не входить до завдань цієї лабораторної роботи).
Перевірка загальної якості рівняння регресії
Для оцінки якості побудованої моделі регресії можна використовувати коефіцієнт детермінації. Коефіцієнт детермінації служить мірою, яка дозволяє визначити: наскільки вдало емпіричне рівняння регресії узгоджується зі статистичними даними; якою мірою варіація залежної змінної визначена варіацією незалежної змінної. На основі коефіцієнта детермінації можна зробити висновок про ступінь значущості вимірюваного зв’язку в економетричній моделі.
Визначення. Коефіцієнт детермінації R2 характеризує частку дисперсії, пояснювану регресією, у загальній дисперсії результативного фактора. Коефіцієнт R2 обчислюють за формулою
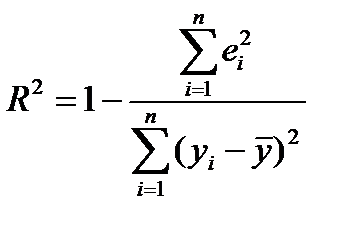або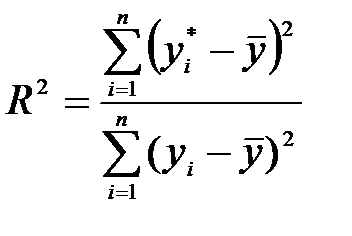 
.
R2 змінюється від нуля до одиниці, тобто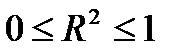 
. За R2=1 виникає функціональний зв'язок, а за R2=0 зв'язок відсутній.
У процесі встановлення того, яке значення R2 можна вважати задовільним у ході оцінки моделі, можна керуватися шкалою Чеддока (табл. 4).
Таблиця 4
| 
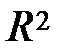
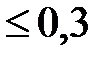
| (0,3–0,5] | (0,5–0,7] | (0,7–0,9] | >0,9 |
| Якість зв’язку | Слабка | Помірна | Значна | Висока | Дуже висока |
Щільність зв’язку певних факторів можна оцінити за допомогою лінійного коефіцієнта парної кореляції rxy. Нагадаємо, що к оефіцієнт парної кореляції rxy служить мірою лінійної асоціативності (лінійного зв’язку) між двома змінними. Його обчислюють за формулою
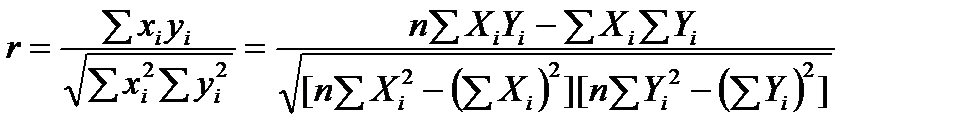
або для випадку парної регресії таким чином:
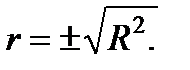
Коефіцієнт кореляції характеризує щільність тільки лінійної залежності й незастосовний для опису нелінійної залежності. Він може набувати значень від – 1 до 1. Хоч r є мірою лінійної асоціативності між двома змінними, це необов’язково означає можливість відображати реальний причинно-наслідковий зв'язок.