Специфікація моделі
Парну регресію застосовують, якщо існує домінуючий фактор, який і виступає пояснювальною змінною. Аналітична форма моделі може бути різною залежно від економічної сутності зв’язків. Розглядають лінійні та нелінійні регресії.
Лінійну регресію описують рівнянням Y = a 0 + a 1 X. Нелінійні регресії поділяються на два класи (табл. 3):
· регресії, нелінійні відносно включених в аналіз пояснювальних змінних, але лінійні за параметрами;
· регресії, нелінійні за параметрами.
Таблиця 3
| Вид регресії | Приклад |
| Регресії, лінійні за параметрами | |
| Поліноми різних степенів |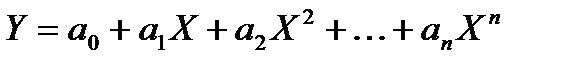 
|
| Рівностороння гіпербола |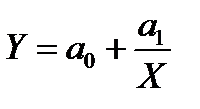 
|
| Регресії, нелінійні за параметрами | |
| Степенева |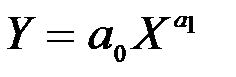 
|
| Показникова |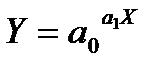 
|
| Експоненціальна |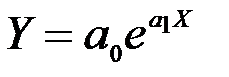 
|
У випадку парної регресії вибір специфікації моделі можна виконати візуально, використовуючи графічне зображення емпіричних даних як точок (xi, yi) на кореляційному полі в декартовій системі координат, які утворюють так звану діаграму розсіювання (рис. 2, а – в). Так, виходячи з рис.2,а можна припустити, що зв’язок між Y та Х є лінійний: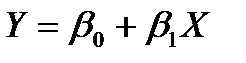 
; зображена на
рис.2,б залежність близька до параболічної: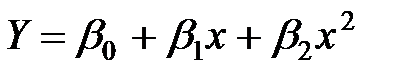 
; на рис.2,в явної залежності між Y та Х не спостерігаємо.
у у y
0 х 0 х 0 х
а б в
Рис. 2. Діаграми розсіювання
Визначення параметрів моделі
Для оцінки параметрів регресій, лінійних за параметрами, застосовують МНК. Метод дозволяє отримати такі оцінки параметрів, за яких сума квадратів відхилень фактичних значень результативної ознаки у від теоретичних значень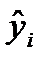 
за тих самих значень фактора х мінімальна, тобто
.
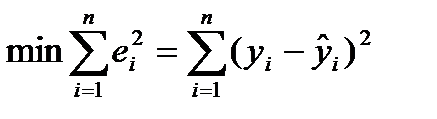Геометричну ілюстрацію МНК показано на рис. 3.
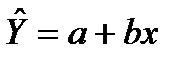
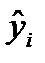
| y i |
| ei |
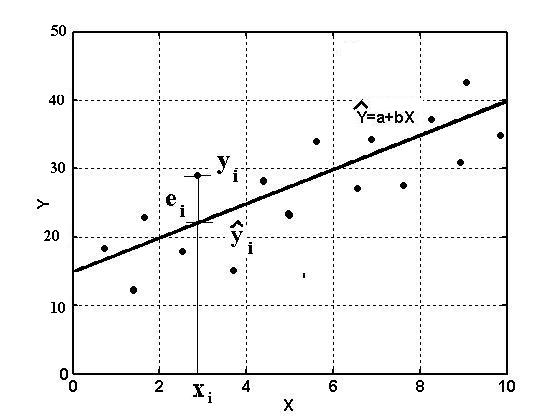
Рис. 3. Геометрична ілюстрація методу найменших квадратів
У випадку лінійної регресії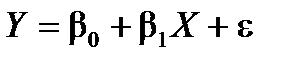 
параметри знаходять із такої системи нормальних рівнянь:
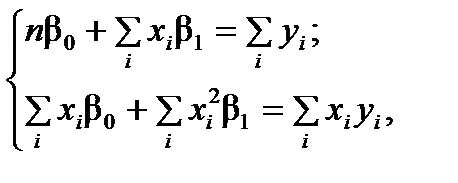
де n – кількість спостережень;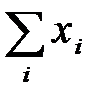 
, 
, 
, 
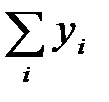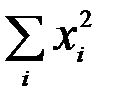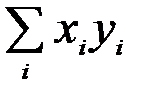– величини, які можна розрахувати на основі вихідних спостережень за змінними Y і X.
Розв’язавши подану систему, одержимо оцінки невідомих параметрів
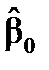і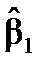 
:
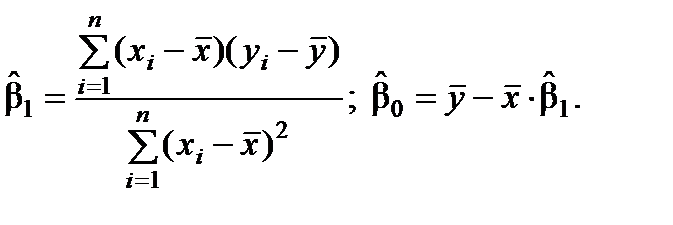
Зауваження .
1. МНК доцільно застосовувати тоді, коли виконуються такі передумови (гіпотези):
а) математичне сподівання залишків дорівнює нулю;
б) значення вектора залишків ε незалежні між собою й мають сталу дисперсію;
в) незалежна змінна моделі не зв’язана із залишками.
Ці гіпотези відомі як умови Гаусса – Маркова. У разі виконання цих умов МНК дозволяє створити найбільш відповідну емпіричним даним модель. Якщо деякі умови не виконуються, то необхідно застосовувати більш складні методи оцінювання.
2. Для нелінійних регресійних моделей, що є нелінійні відносно пояснювальної змінної, але лінійні за параметрами, МНК застосовують так само, як і у випадку лінійної регресії. До регресії, нелінійної за оцінюваними параметрами, залежно від вигляду функції можна застосовувати лінеаризуюче перетворення (буде описано далі).