Лабораторна робота 2 Економетрична модель із двома змінними: побудова і аналіз
Виконавши цю роботу, ви навчитеся:
· будувати парну лінійну економетричну модель;
· перевіряти статистичну значущість коефіцієнтів моделі;
· перевіряти статистичну значущість моделі;
· визначати точність моделі;
· аналізувати зв’язок між змінними за допомогою отриманого рівняння регресії та здійснювати прогнозування.
Ключові поняття: регресія; результативний фактор (ендогенна змінна); фактор-ознака (екзогенна змінна); стохастична складова регресії; коефіцієнт кореляції; специфікація моделі; метод найменших квадратів (МНК); система нормальних рівнянь; стандартна похибка параметрів моделі; статистична значущість оцінок параметрів моделі; t-критерій; довірчий інтервал; значущість економетричної моделі; F-критерій; залишкова дисперсія; коефіцієнт детермінації; інтервальний прогноз; точковий прогноз; похибка прогнозу.
Теоретичні відомості
Серед численних зв’язків між економічними показниками завжди можна виділити такий показник, вплив якого на результативну ознаку є основний, найбільш важливий. Щоб виміряти цей зв’язок кількісно, необхідно побудувати економетричну модель із двома змінними (просту модель).
Визначення. Економетричну модель, у рівняння якої включено лише одну пояснювальну змінну, називають парною. Загальний вигляд моделі такий:
Y = f (X, ε),
де Y – залежна змінна (результативна ознака); X – незалежна змінна (фактор);
ε – стохастична складова.
Постановка задачі. За даними n спостережень за спільною зміною двох параметрів х та у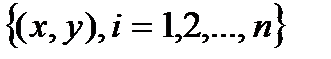 
необхідно визначити аналітичну залежність 
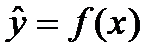, яка б щонайкраще описувала дані спостереження.
Розв’язування задачі побудови якісної математичної моделі у формі рівняння регресії на основі певної вибірки можна умовно поділити на такі три етапи:
1) специфікація моделі (вибір форми рівняння регресії);
2) оцінка параметрів, які є складовими частинами вибраного рівняння;
3) аналіз якості рівняння математичної моделі досліджуваного процесу та перевірка моделі на адекватність (відповідність емпіричним даним) із можливим наступним удосконаленням специфікації рівняння зв’язку.