Тема урока: Решение задач с помощью рациональных уравнений
14.02.2022
Алгебра
8-А, Б, В классы
Тема урока: Решение задач с помощью рациональных уравнений
Ребята, откройте рабочие тетради. Запишите:
Четырнадцатое февраля
Классная работа
Решение задач с помощью рациональных уравнений
Посмотрите видео по ссылке
https://resh.edu.ru/subject/lesson/1979/main/
Запишите решение задач в тетрадь
Задача №1.
При совместной работе двух программистов программа была написана за 6 ч. Сколько времени потребовалось бы каждому программисту отдельно для написания программы, если первому программисту для этого требуется на 5 часов больше, чем второму?
Составим таблицу с данными по основным величинам: производительность (скорость работы), время и работа.
| Производительность | Время | Работа | |
| Программист 1 | 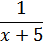
| х + 5 ч. | 1 |
| Программист 2 | 
| х ч. | 1 |
| Совместная работа | 
| 6 ч. | 1 |
Запишем уравнение, отражающее производительность при совместной работе двух программистов
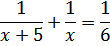
По смыслу задачи х ≠ 0 и х ≠ 5. Умножим обе части уравнения на наименьший общий знаменатель дробей 6х(х + 5)
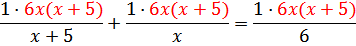
После преобразований, решим уравнение
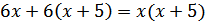
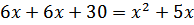
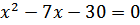
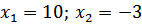
Значение –3 не подходит по смыслу задачи, значит, второй программист напишет программу за 10 часов, а первый потратит на 5 часов больше, то есть 15 часов.
Ответ: t1 = 15ч; t2 = 10ч.
Задача №2.
В лимонад добавили 150 граммов воды. В результате концентрация сахара в лимонаде уменьшилась на 3%. Определим первоначальную массу лимонада, если известно, что в нём содержалось 65 граммов сахара.
Основные величины задачи: масса лимонада, масса сахара и концентрация сахара. Составим таблицу
| Масса лимонада | Масса сахара | Концентрация сахара | |
| Лимонад | х г | 65 г | 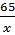 ·100% ·100%
|
| Лимонад с добавлением воды | х + 150 г | 65 г | 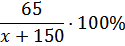
|
Запишем уравнение
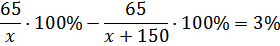
По смыслу задачи х ≠ 0 и х ≠ –150. Умножим обе части уравнения на наименьший общий знаменатель дробей х(х + 150)
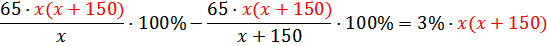
После преобразований, решим уравнение
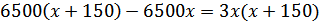
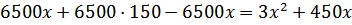
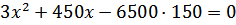
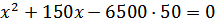
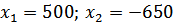
Значение –650 не подходит по смыслу задачи, значит, первоначальная масса лимонада 500 граммов.
Ответ: 500 граммов
Задача №3
Моторная лодка прошла 25 км по течению реки и 3 км против течения, затратив на весь путь 2 ч. Какова скорость лодки в стоячей воде, если скорость течения реки равна 3 км/ч?
Пусть х км/ч – скорость скорость лодки в стоячей воде.
| V, км/ч | t,ч | S, км | |
| По течению | х+3 | 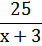
| 25 |
| Против течения | х-3 | 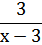
| 3 |
Запишем уравнение
– Приводим дроби к общему знаменателю, расставляем дополнительные множители и решаем.
25(х–3)+3(х+3)=2(х+3)(х–3)
– Раскрываем скобки, приводим подобные слагаемые.
25х – 75+3х+9 –2х2+6х–6х+18=0
–2х2 +28х –48=0
– Разделим уравнение на –2.
х2–14х+24=0
– Найдем корни уравнения.
D=196–4*24*1=100
Х1,2= 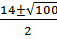 =
= 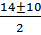
х1= 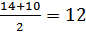
х2= 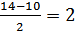
ООУ: х 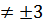
– Решив уравнение мы нашли корни х1=12 и х2=2.
– По смыслу задачи скорость лодки в стоячей воде должна должна быть больше скорости течения. Этому условию удовлетворяет первый корень – число 12 и не удовлетворяет второй.
Ответ: 12 км/ч.
Домашнее задание: повторить п.26, решить № 619, 628








