Частина 1. Загальні питання автоматизованого електропривода
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ
КАФЕДРА КОМП’ЮТЕРНИХ НАУК
СЕКЦІЯ КОМП’ЮТЕРИЗОВАНИХ СИСТЕМ УПРАВЛІННЯ
ОБОВ’ЯЗКОВЕ ДОМАШНЄ ЗАВДАННЯ
з дисципліни: «Електронні системи автоматичного керування та електроприводи»
Варіант №17
Виконав
студент групи СУ-01 Паламарчук О. І.
Перевірив Черв’яков В. Д.
СУМИ 2014
Зміст
ЧАСТИНА 1. ЗАГАЛЬНІ ПИТАННЯ АВТОМАТИЗОВАНОГО ЕЛЕКТРОПРИВОДА 3
Задача №1. 3
Задача №2. 4
Задача №3. 5
Задача №4. 7
ЧАСТИНА 2. МЕХАНІКА ЕЛЕКТРОПРИВОДА.. 13
Задача №1. 13
Задача №2. 14
Задача №3. 16
Задача №4. 21
Задача №5. 24
Задача №6. 27
Задача №7. 31
Задача №8. 34
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ.. 36
ЧАСТИНА 1. ЗАГАЛЬНІ ПИТАННЯ АВТОМАТИЗОВАНОГО ЕЛЕКТРОПРИВОДА
Задача №1
Керований тиристорний перетворювач (рис 1) має внутрішній опір Rп=0,15 Ом. Анодна напруга U=260 В. Потрібно побудувати зовнішню характеристику перетворювача при значенні кута управління a=42 ел. град.

Розв ’ язок:
Зовнішньою характеристикою перетворювача змінного струму в постійний називається функціональна залежність Ud(Id) випрямленої напруги від випрямленого струму. В нашому випадку схема випрямлення – трьохфазна нульова, тому схемний коефіцієнт kсх=1,17. Для цієї схеми максимальна випрямлена е.р.с. (при a=0 ел. град.)
Еd0=kсхU=1,17*260=304,2 B
Випрямлена е.р.с. при заданому значенні a=54 ел. град.
Еd=Еd0cos420=304,2*0,74=225,1 В
Рівняння зовнішньої характеристики перетворювача має вигляд лінійної функції
Ud=Ed-RпId=225,1 - 0,15Id.
Графік зовнішньої характеристики (рис 2.) представляє пряму лінію, яка проходить через точки з координатами (Udo;0) і (0;Iкз), де Udo= Еd = 225,1 В – напруга холостого ходу,
Iкз= Еd/Rп=225,1/0,15=1500,7 А.
Областю визначення струму являється інтервал дійсних чисел [0;∞).
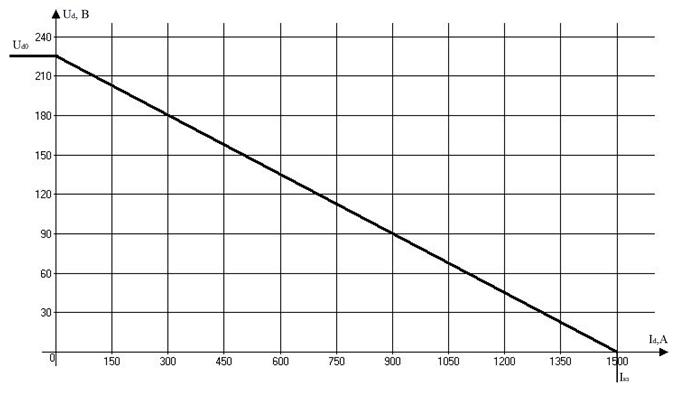
Рисунок 2
Задача №2
Якір двигуна постійного струму з незалежним збудженням підключений до нереверсивного керованого тиристорного перетворювача. Анодна напруга U=260 В. Еквівалентний опір якірного ланцюгу Rе=Rя+Rп+Rд, де Rя=0,03 Ом – опір якірного ланцюгу двигуна, Rп=0,05 Ом – внутрішній опір перетворювача, Rд=0,75 Ом – опір додаткового резистора в якірному ланцюзі. Потрібно визначити значення кута α управління тиристорного перетворювача, при якому випрямлена напруга Ud=k1Еd0, , якщо двигун працює у руховому режимі при значенні е.р.с. якоря Ея=k2Еd0, де Еd0 – максимальна випрямлена е.р.с. Значення коефіцієнтів k1=0,8, k2=0,6.
Розв’язок:
Перетворювач виконаний за трифазною нульовою схемою, тому схемний коефіцієнт kcx=1,17. Максимальна випрямлена е.р.с.: Ed0=kcxU=1,17*260=304,2 В, а випрямлена напруга: Ud=0,8Ed0=0,8*304,2=243,36 В.
Е.р.с. якоря: Eя= k2Еd0=0,6*304,2=182,52 В
Рівняння електричного стану ланцюгу якоря має вигляд:
Ud=Eя+(Rя+Rд)Id
З цього рівняння маємо змогу визначити значення струму якорю (випрямленого струму):
Id =( Ud- Eя)/( Rя +Rд)=(243,36-182,52)/(0,03+0,75)=78 А.
Випрямлена е.р.с. перетворювача:
Еd= Ud+ Rп Id=243,36+0,05*78=247,26 В.
Кут управління перетворювача:
α=arcos(Еd/ Еd0)= arcos(247,26/304,2)=35,63 ел. град.
Відповідь: α=35,63 ел.град.
Задача №3
Якір двигуна постійного струму з незалежним збудженням підключений до нереверсивного керованого тиристорного перетворювача. Двигун працює в генераторному режимі, перетворюючи механічну енергію в електричну, яка передається в живильну мережу через тиристорний перетворювач. При цьому останній працює в інверторному режимі. Індуктивність фази трансформатора Lт=0,001 Гн. Частота напруги живильної мережі f=50 Гц. Анодна напруга U=260 В. Опір якірного ланцюгу двигуна Rдв=Rя+Rд, де Rд=1,0 Ом. Двигун розвиває електромагнітну потужність Pем. Значення Rя=0,3 Ом та Pем=4,5 кВт. Потрібно визначити значення кута α управління тиристорного перетворювача, якщо е.р.с. Eя якоря двигуна за величиною дорівнює анодній напрузі U; накреслити характеристику управління перетворювача Еd(α) і вказати на неї робочу точку , що відповідає заданому режиму роботи двигуна.
Розв’язок:
Зважаючи на режими роботи двигуна і перетворювача, при обраних позитивних напрямках е.р.с. Еd перетворювача, випрямленій напрузі Ud, струму Id та е.р.с. Eя якоря двигуна (рис.1), маємо: Id>0, Еd<0, Eя<0, Pем<0, тобто Pем= - 4,5кВт, Eя= - U= -260 В.
Використовуючи відому рівність Pем= Eя Id, визначимо струм якоря двигуна:
Id= Pем/ Eя= - 4,5*103/(-260)=17,31 А.
Еквівалентний опір перетворювача:
Rп=(m/(2π))xт= mf Lт =3*50*0,001=0,15 Ом,
де m=3 – кількість фаз; xт»2 π f Lт – індуктивний опір фази трансформатора, приведений до вторинного ланцюгу.
Еквівалентний опір ланцюгу випрямленого струму:
Rе= Rдв+ Rп= Rя+ Rд+ Rп=0,3+1+0,15=1,45 Ом.
Е.р.с. перетворювача визначимо із рівняння електричного стану якірного ланцюгу двигуна:
Еd= Eя+ Id Rе= - 260+17,31*1,45= -234,9 В.
Перетворювач виконаний за трьохфазною нульовою схемою, тому схемний коефіцієнт kсх=1,17. Максимальна випрямлена е.р.с.:
Еd0=kсхU=1,17*260=304,2 В, а косинус кута управління
cos α=Еd/ Еd0= -234,9/304,2= -0,77.
Кут управління тиристорного перетворювача:
α=arcos(-0,77)=140,35 ел. град.
На рис.3 наведена характеристика управління перетворювача, на якої показана робоча точка з координатами (140,35; -234,9), що відповідає заданому режиму роботи двигуна.
Рисунок 3
| ||||||
| ||||||
 | ||||||
| ||||||
Задача №4
Якір двигуна постійного струму з незалежним збудженням підключений до реверсивного керованого тиристорного перетворювача. Потрібно:
1) Відповідно заданому варіанту, обрати відомості про схему випрямлення, лінійну напругу Uлм трьохфазної живильної мережі і тип двигуна, накреслити електричну схему силової частини електропривода, навести паспортні дані двигуна;
2) визначити розрахункові параметри силового трансформатора, обрати останній з таблиці та навести його паспортні дані (значення коефіцієнтів, що зв'язують параметри трансформатора зі струмами та напругами у схемі перетворювача, наведені в таблиці). Допускається користування довідниками та каталогами, з посиланням на джерело інформації;
3) визначити розрахункові параметри тиристорів та зробити їх вибір з таблиці;
4) розрахувати індуктивність зрівнювальних реакторів (для обмеження зрівнювального струму).
Лінійна напруга Uлм=220 В; тип двигуна Д12; Рн=2,5 кВт; Uн=220 В; Iн=14,6А; nн=1140 об/хв.
Розв’язок:
Як слідує з умов задачі, реверсивний тиристорний перетворювач виконаний за трьохфазною нульовою схемою випрямлення зі зрівнювальними реакторами. Це означає, що здійснюється погоджене управління вентильними групами перетворювача. Оскільки з умов задачі передбачається використання двохобмоткового трьохфазного трансформатора, то живлення обох вентильних груп перетворювача має здійснюватись від однієї його вторинної обмотки.
Електрична схема силової частини електропривода наведена на рис.4.
Вибір трансформатора для живлення вентильного перетворювача здійснюється по розрахункових значеннях фазних струмів I1 та I2 відповідно в його первинній та вторинній обмотках, вторинної фазної е.р.с. E2 і типової потужності Sт.
Зробимо розрахунок параметрів трансформатора та вибір останнього в схемі рис.4. Теоретичне значення вторинної фазної е.р.с.:
E2т=kнUd=kнUн,
де kн=0,922 - схемний коефіцієнт для реверсивного вентильного перетворювача з трьохфазною нульовою схемою випрямлення, навантаженого на противо-е.р.с. при погодженому управлінні вентильними групами, що враховує схему випрямлення та мінімально допустиме значення кута управління інверторної групи; Ud – потрібне значення випрямленої напруги.
З урахуванням запасів розрахункове значення вторинної фазної напруги:
U2фр=kukakrE2т=kukakrkнUн=1,1×1,1×1,05×0,922×220=257,708 В,
де ku=1,1 і ka=1,05÷1,15 - коефіцієнти запасів, якими враховуються, відповідно, можливі коливання напруги живильної мережі та кутів управління вентильних груп, а коефіцієнтом kr=1,05 враховуються падіння напруги в обмотках трансформатора, вентилях та з'єднувальних проводах.
Розрахункове значення вторинної лінійної напруги:
U2лр= 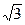 U2фр=1,732×257,708=446,351 В.
U2фр=1,732×257,708=446,351 В.
Типова потужність трансформатора:
Sт=kмUdId=kмUнIн=1,45×220×14,6=4,657 кВА,
де kм=1,45 – схемний коефіцієнт (табл. 2.2).
Розрахункова потужність трансформатора:
Sр=kukakіSт=1,1×1,1×1,05×4,657=5,92 кВА,
де kі=1,05¸1,1 - коефіцієнт, що враховує відхилення форми струмів вентилів від прямокутної.
Трансформатор обирається з урахуванням співвідношень Sн³Sр, U2н³0,85×U2лр=379,4 U1н=Uлм, де Sн, U2н, U1н та Uлм– відповідно номінальні значення його потужності, вторинної та первинної лінійних напруг і лінійної напруги живильної мережі.
Оберемо трансформатор типу ТТ-11 потужністю 11 кВА. Схема з'єднання обмоток - Ү/Ү. Номінальні первинна та вторинна напруги цього трансформатора відповідно дорівнюють: U1н=220 В; U2н=400 В. Співвідношення Sн³Sр та U2н³0,85×U2лр виконуються. Для перевірки обраного трансформатора за струмової навантаженості обмоток зробимо наступні розрахунки.
Номінальний струм фази первинної обмотки трансформатора (з урахуванням схеми з'єднання фаз цієї обмотки):
I1фн=Sн/ 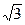 U1н=11×103/(1,73×220)=28,9 A.
U1н=11×103/(1,73×220)=28,9 A.
Номінальний струм фази вторинної обмотки трансформатора (з урахуванням схеми з'єднання фаз цієї обмотки):
I2фн=Sн/ 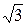 U2н=11×103/(1,73×400)=15,9A.
U2н=11×103/(1,73×400)=15,9A.
Коефіцієнт трансформації:
kтр=U1н/U2н=220/400=0,55.
Розрахункове діюче значення струму вторинної обмотки трансформатора: I2р=kikт2Id=kikт2Iн=1,05*0,577*14,6=8,86 А, а розрахункове діюче значення струму первинної обмотки:
I1р=kikт1Id/kтр =ki(kт1/kтр)Iн=1,05×(0,471/0,55)×14,6=13,13 А.
Обраний трансформатор проходить за струмовому навантаженню обмоток, оскільки виконуються співвідношення I1н³I1р і I2н³I2р (трансформатор має потужність більш за двократну в порівнянні з Sр через обмеженість вибору за таблицею).
Зробимо розрахунок параметрів та вибір тиристорів у схемі рис.4.
Середнє значення струму вентиля (тиристора):
Iвс=kтвId=kтвIн,
де kтв=0,333 – схемний коефіцієнт, а розрахункове значення номінального струму вентиля:
Iвр=kвIвс= kвkтвIн=1,2×0,333×14,6=5,83 А,
де kв=1,1¸1,3 – коефіцієнт запасу, вибір якого призводять з урахуванням умов охолодження вентиля та пускового струму двигуна.
Розрахункове значення максимальної зворотної напруги, що прикладається до вентиля:
Uв.макс.=kukakrkнвUd=1,1×1,1×1,05×2,25×220=628,89 В,
де kнв=Uв.макс.т/Ud=2,25 – схемний коефіцієнт;
Uв.макс.т=kнв×Ud – теоретичне значення зворотної напруги;
Ud=Uн=220 В.
У системах електропривода широко застосовуються лавинні тиристори серії ТЛ. Вони здібні витримувати значні перевантаження з напруги зворотного напряму, мають високу термостабільність, здібні витримувати великі швидкості зростання прямої напруги. призведемо вибір тиристорів цієї серії.
Номінальна напруга вентиля, тобто добуток класу вентиля на 100, має бути не менш як Uв.макс.=628,89 В, а номінальний струм вентиля має бути не менш як Iвр=5,83А. Тому обираємо тиристори типу ТЛ-150 7-го класу, з примусовим охолодженням.
Призведемо розрахунок індуктивності зрівнювальних реакторів у схемі. Сумарна індуктивність 2Lур двох реакторів, що необхідна для обмеження статичного зрівнювального струму Iур (середнього значення зрівнювального струму) в реверсивних вентильних перетворювачах, визначається за формулою:
2Lур= 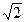 U2фkур/wIур.макс.,
U2фkур/wIур.макс.,
де Lур - індуктивність одного реактора (2Lур – сумарна індуктивність двох реакторів);
U2ф – фазна напруга вторинної обмотки трансформатора;
Iур.макс. – максимально допустиме значення зрівнювального струму;
w=2pf=314 рад/с – кругова частота живильної мережі при стандартній частоті
f=50 Гц ;
kур – розрахунковий коефіцієнт (kур»0,65 для нульових схем випрямлення і kур»0,18 для мостових схем).
Значення Iур.макс. зрівнювального струму приймають таким, що дорівнює (0,1 – 0,3)Iн, причому при достатніх запасах за струмом вентилей та при відсутності спеціальних вимог до енергетичних показників електроприводу слід приймати більші значення Iур.макс.. Ми приймемо Iур.макс.=0,2×Iн=0,2*14,6=2,92 А.
Для реакторів, що не насичуються (з великим зазором) і насичуються, індуктивність кожного з двох реакторів відповідно дорівнює Lур та 2Lур. З ціллю мінімізації габаритів звичайно обирають реактори, що насичуються частково. Ми приймаємо саме таке рішення. У цьому випадку
Lур=0,7×2×Lур=0,7× 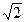 ×U2нkур/(
×U2нkур/( 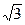 ×wIур.макс.)=
×wIур.макс.)=
=(0,7× 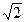 ×400×0,65)/(
×400×0,65)/( 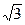 ×314×2,92)=152,05/348,07=0,1621 Гн.
×314×2,92)=152,05/348,07=0,1621 Гн.
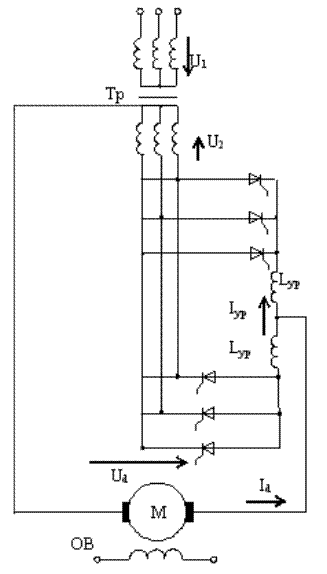
Рисунок 4
ЧАСТИНА 2. МЕХАНІКА ЕЛЕКТРОПРИВОДА
Задача №1
Визначити момент інерції шестерні (рис.1), виготовленої з чавуну, питома вага якого γ = 7,2 т/м3. Варіанти геометричних розмірів шестерні наведені в таблиці (n – кількість отворів, що рівномірно розподілені по колу шестерні).
Таблиця 1
| Номер варіанта | n | Розміри шестерні, мм | ||||||||
| h1 | h2 | h3 | r1 | r2 | r3 | r4 | r5 | r6 | ||
| 17 | 6 | 150 | 100 | 40 | 600 | 550 | 140 | 300 | 80 | 100 |
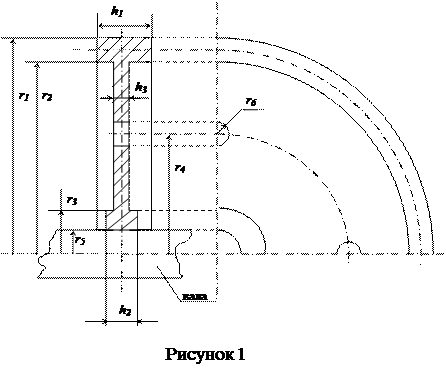
Розв’язок:
Визначимо момент інерції вінця шестерні за формулою
Jв = 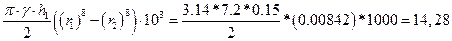 ,
,
після підстановки даних дає результат: Jв = 14,28 кг∙м2.
Визначимо момент інерції тіла шестерні за формулою
Jт = 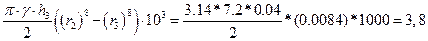 ,
,
після підстановки даних дає результат: Jт = 3,8 кг∙м2.
Визначимо момент інерції ступиці шестерні за формулою
Jс = 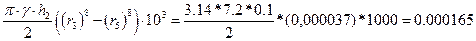 ,
,
після підстановки даних дає результат: Jс = 0.000165 кг∙м2.
Вважаючи що отвори на шестерні зробленими з того ж матеріалу, що й сама шестерня, за формулою
Jмо = 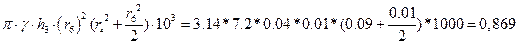 ,
,
визначимо момент інерції одного монтажного отвору: Jмо = 0.869 кг∙м2.
Спільний момент інерції шестерні
Jм = Jв + Jт + Jс -6Jмо = 14,28+3,8 +0.000165–6*0,869 = 12,87 кг∙м2.
Задача №2
Визначити момент інерції шківа зі спицями (рис. 2), виготовленого зі сталі, питома вага якої γ = 7,8 т/м3. Варіанти геометричних розмірів шківа наведені в табл.2 (n – кількість спиць, що рівномірно розподілені по колу шківа, d – діаметр спиць).
Таблиця 2
| Номер варіанта | n | Розміри шківа, мм | ||||||
| h1 | h2 | d | r1 | r2 | r3 | r 4 | ||
| 17 | 6 | 150 | 100 | 40 | 600 | 550 | 140 | 80 |
Розв’язок:
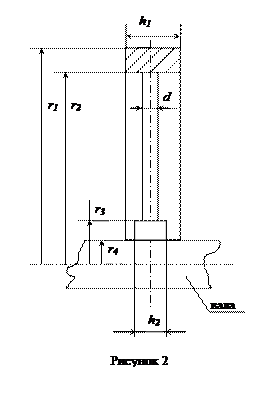
Визначаємо момент інерції вінця шківа за формулою
Jв = 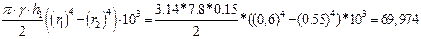 (кг∙м2),
(кг∙м2),
Визначаємо момент інерції спиці шківа за формулою
Jст = 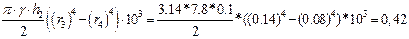 (кг∙м2),
(кг∙м2),
Припустимо що шків суцільний. Визначимо момент інерції тіла шківа за формулою
Jсуц = 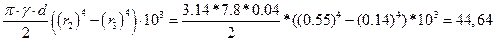 (кг∙м2),
(кг∙м2),
Щоб знайти момент інерцій однієї спиці знайдемо коефіцієнт пропорційності який дорівнює відношенню об’єму суцільного тіла до об’єму однієї спиці
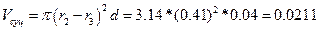 (м3),
(м3),
Vc= 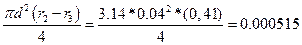 (м3)
(м3)
k= 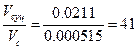
Знайдемо момент інерцій однієї спиці 
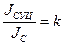
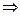
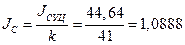
Спільний момент інерції шківа
 J = Jв + Jст +6*Jс = 69,974+0,42+6*1,0888 = 76,927 (кг∙м2).
J = Jв + Jст +6*Jс = 69,974+0,42+6*1,0888 = 76,927 (кг∙м2).
Задача №3
На рис. 3 показана кінематична схема електропривода ліфта. Вала двигуна 2 пов’язана з гальмом 1 і через муфту 3 з вхідною валою знижуючого од-ноступінчатого редуктора 4. Вихідна вала редуктора з’єднана з канатоведучим шківом 5. Канатоведучий шків 7 приводиться в рух канатом і забезпечує натяг останнього, достатній для стійкого руху кабіни 6 ліфта в спрямовуючих і противаги 8.
Обчислити приведений до швидкості обертання двигуна 2 підсумовний момент інерції 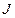 механічної частини електропривода і статичний момент
механічної частини електропривода і статичний момент 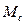 на валі двигуна при русі кабіни 6 ліфта «вгору» і «вниз», якщо задані (див. табл. 1): маса
на валі двигуна при русі кабіни 6 ліфта «вгору» і «вниз», якщо задані (див. табл. 1): маса 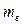 вантажу, маса
вантажу, маса 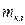 кабіни, маса
кабіни, маса 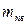 противаги 8, швидкість
противаги 8, швидкість 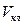 руху кабіни 6 ліфта, діаметр
руху кабіни 6 ліфта, діаметр 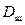 канатоведучих шківів 5 і 7, передатне число
канатоведучих шківів 5 і 7, передатне число 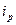 редуктора 4, ККД
редуктора 4, ККД 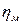 механічної частини електропривода, довжина
механічної частини електропривода, довжина 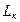 канату, маса
канату, маса 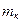 погонного метра канату, коефіцієнт жорсткості одного метра канату
погонного метра канату, коефіцієнт жорсткості одного метра канату 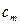 , підсумовний момент інерції
, підсумовний момент інерції 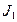 елементів, що обертаються зі швидкістю
елементів, що обертаються зі швидкістю  , підсумовний момент інерції
, підсумовний момент інерції  елементів, що обертаються зі швидкістю
елементів, що обертаються зі швидкістю  . Кабіна 6 ліфта порожня при русі «вгору» і завантажена при русі «вниз» (цю обставину необхідно мати на увазі при визначенні режимів роботи двигуна).
. Кабіна 6 ліфта порожня при русі «вгору» і завантажена при русі «вниз» (цю обставину необхідно мати на увазі при визначенні режимів роботи двигуна).
Скласти розрахункову кінематичну схему електропривода у вигляді двомасової пружної системи з урахуванням пружності канату, незважаючи на податність валів. Визначити параметри розрахункової кінематичної схеми. Скласти математичну модель механічной частини електропривода у вигляді системи рівнянь руху і структурной схеми. Визначити частоту власних коливань двомасової пружної системи. Розглянути питання про можливість спрощення розрахункової кінематичної схеми електропривода ліфта до жорсткої (одномасової) системи.
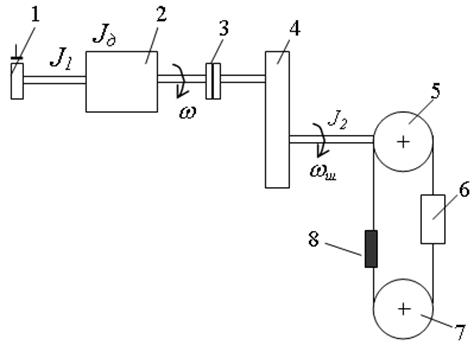
Рисунок 3
Таблиця 3
| Номер варіанта | 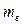 ,
т ,
т
| 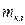 ,
т ,
т
| 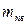 ,
т ,
т
| 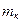 ,
кг ,
кг
| 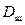 ,
м ,
м
| 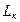 ,
м ,
м
| 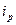
| 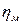
| 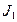 ,
кг*м ,
кг*м 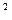
| 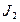 ,
кг*м ,
кг*м 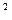
| 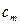 ,
Н/м ,
Н/м
|
| 17 | 0,5 | 0,2 | 0,23 | 180 | 0,8 | 40 | 32 | 0,8 | 0,36 | 2,4 | 1*108 |
Розв’язок:
Здійснимо приведення параметрів обертальних елементів привода до швидкості ω обертання двигуна 2. Елементи 4-5 мають швидкість обертання, яка відрізняється від ω. Передаточне число редуктора має значення i р=32. Приведення моментів інерції та жорсткостей обертальних елементів привода здійснюється за формулами:
J пр.і = 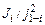 ,
,
спр.і = 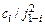 .
.
Кабіна ліфта 6 рухається зі швидкістю V кл. Для кабіни ліфта радіус приведення дорівнює
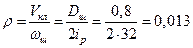 (м),
(м),
де w ш -швидкість обертання канатоведучих шківів 5 і 7,
D ш- діаметр канатоведучих шківів,
i р- передаточне число редуктора 4.
Приведений до вала двигуна момент інерції:
при русі кабіни “вгору”
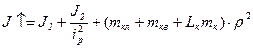 ,
,
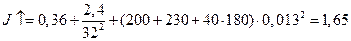 кг*м
кг*м 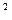 ,
,
при русі кабіни “вниз”
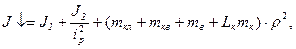
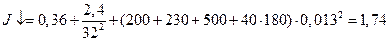 кг*м
кг*м 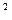 .
.
Приведена жорсткість канату:
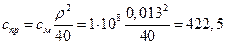 Н∙м.
Н∙м.
Статичний момент, який долає двигун при підйомі кабіни ліфта:
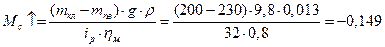 Н∙м.
Н∙м.
Статичний момент, який долає двигун при спуску кабіни ліфта:
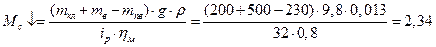 Н∙м.
Н∙м.
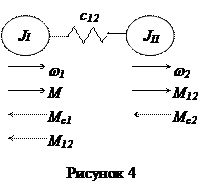 Розрахункова кінематична схема двомасової механічної частини електропривода подана на рис. 4, де JI, JII – моменти інерції першої та другої мас, з'єднаних пружним зв'язком з коеффіцієнтом жорсткості с12; w 1 і w 2 – швидкості обертання першої та другої мас; М – електромагнітний момент двигуна; Мс1 та Мс2 – статичні моменти опору, що діють відповідно на першу та другу маси; М12 – пружний момент.
Розрахункова кінематична схема двомасової механічної частини електропривода подана на рис. 4, де JI, JII – моменти інерції першої та другої мас, з'єднаних пружним зв'язком з коеффіцієнтом жорсткості с12; w 1 і w 2 – швидкості обертання першої та другої мас; М – електромагнітний момент двигуна; Мс1 та Мс2 – статичні моменти опору, що діють відповідно на першу та другу маси; М12 – пружний момент.
Визначимо параметри розрахункової кінематичної схеми при русі кабіни «вгору»:
Моменти інерції першої та другої мас:
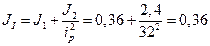 кг∙м2,
кг∙м2,
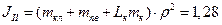 кг∙м2;
кг∙м2;
Cтатичні моменти опору:
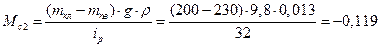 Н∙м.
Н∙м.
Мс1 = Мс 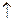 -Мс2= - 0,149+0,119 = - 0,03 Н∙м.
-Мс2= - 0,149+0,119 = - 0,03 Н∙м.
Визначимо параметри розрахункової кінематичної схеми при русі кабіни «вниз»:
Моменти інерції першої та другої мас:
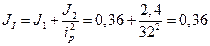 кг∙м2,
кг∙м2,
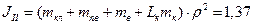 кг∙м2;
кг∙м2;
Cтатичні моменти опору:
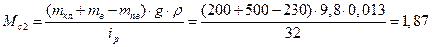 Н∙м.
Н∙м.
Мс1 = Мс 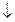 -Мс2=2,34-1,87=0,47 Н∙м.
-Мс2=2,34-1,87=0,47 Н∙м.
Математична модель механічної системи рис. 4 має вигляд системи рівнянь руху:
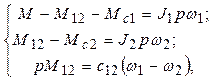
де р = d/dt - оператор диференціювання за часом.
Математична модель механічної системи рис. 4. у вигляді структурної схеми на рис.5.
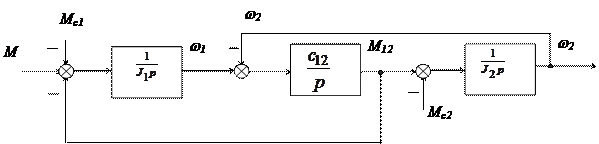 |
Рисунок 5
Рух багатомасових механічних систем з пружними зв'язками може супроводжуватись резонансними явищами. Резонансні частоти системи можуть бути визначені шляхом аналізу структурних схем методами теорії автоматичного керування. Резонансна частота двомасової системи (обертального руху):
W12 = 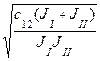
При русі кабіни в вгору:
W12 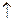 =
= 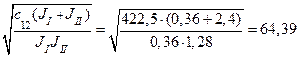 рад/с.
рад/с.
При русі кабіни вниз:
W12 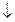 =
= 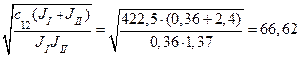 рад/с.
рад/с.
Можливість спрощення моделі механічної частини електроприводу, тобто представлення останньої у вигляді одномасової (жорсткої) системи, можна оцініти:
При русі кабіни в вгору:
γ 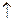 = ( JI + JII )/ JI = (0,36 + 1,28)/0,36=4,56
= ( JI + JII )/ JI = (0,36 + 1,28)/0,36=4,56
При русі кабіни вниз:
γ 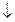 = ( JI + JII )/ JI = (0,36 + 1,37)/0,36=4,8
= ( JI + JII )/ JI = (0,36 + 1,37)/0,36=4,8
Оскільки значення γ незначно перевищує одиницю, то можемо вважати
JII << JI. У такому випадку можна без помітної погрішності представити механічну частину електропривода жорсткою приведеною ланкою (рис. 6), сумарний момент інерції якої:
При русі кабіни в вгору:
Ј S 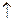 = JI + JII =0,36+1,28 = 1,64 кг∙м2,
= JI + JII =0,36+1,28 = 1,64 кг∙м2,
При русі кабіни вниз:
Ј S 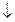 = JI + JII =0,36+1,37 = 1,73 кг∙м2,
= JI + JII =0,36+1,37 = 1,73 кг∙м2,
а сумарний момент навантаження відповідно напряму руху вгору вниз:
Мс 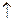 = Мс1 + Мс2 = - 0,149+0,119 = - 0,03 Н∙м.
= Мс1 + Мс2 = - 0,149+0,119 = - 0,03 Н∙м.
Мс 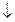 = Мс1 + Мс2 = 2,34-1,87=0,4 Н∙м.
= Мс1 + Мс2 = 2,34-1,87=0,4 Н∙м.
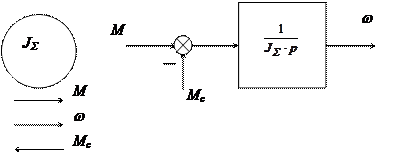 |
Рисунок 6
Рівняння руху одномасової системи (рис 5) має вигляд:
M – Mc = J S∙∙p w .
Задача №4
На рис. 7 наведено кінематичну схему механічної частини електроприводу пересування візка мостового крану, де 1 – ходові колеса, 2 – гальмо, 3 – двигун, 4 – з’єднувальна муфта, 5 – рейки.
Знехтуючи податністю механічних зв’язків, визначити приведений до швидкості обертання двигуна статичний момент 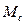 , електромагнітний момент
, електромагнітний момент 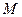 двигуна та його динамічну складову
двигуна та його динамічну складову 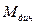 в процесах сталого руху, розгону і гальмування, якщо задані (див. табл 4 і 5): суспільна маса візка з вантажем
в процесах сталого руху, розгону і гальмування, якщо задані (див. табл 4 і 5): суспільна маса візка з вантажем 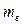 ; діаметр ходових колес
; діаметр ходових колес 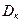 ; діаметр
; діаметр 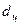 цапф підшипників ходових колес, момент інерції ротора двигуна
цапф підшипників ходових колес, момент інерції ротора двигуна 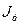 , момекнт інерції решти мас обертального руху
, момекнт інерції решти мас обертального руху 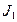 ,
, 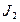 і
і 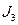 ; числа зубців шестерен редуктора
; числа зубців шестерен редуктора 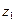 ,
, 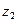 ,
, 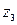 і
і 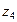 ; ККД однієї шестеренної пари
; ККД однієї шестеренної пари 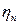 , коефіцієнт
, коефіцієнт 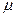 тертя в опорах ходових колес, коефіцієнт
тертя в опорах ходових колес, коефіцієнт 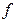 тертя кочіння ходових колес, коефіцієнт
тертя кочіння ходових колес, коефіцієнт 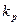 , що враховує тертя реборд колес об рейки, прискорення (лінійне)
, що враховує тертя реборд колес об рейки, прискорення (лінійне) 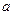 поступового руху візка в процесах розгону і гальмування.
поступового руху візка в процесах розгону і гальмування.
Скласти розрахункову кінематичну схему електропривода у вигляді жорсткої (одномасової) системи. Визначити параметри розрахункової кінематичної схеми. Скласти математичну модель механічної частини електропривода у вигляді рівняння руху і структурної схеми.
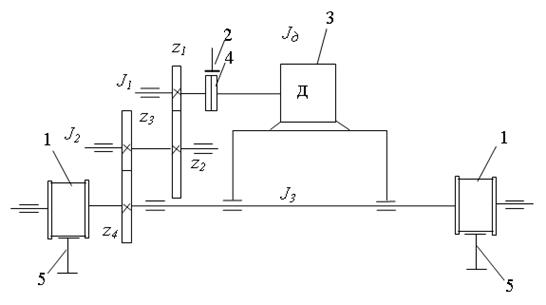
Рисунок 7
Таблиця 4
| Номер варіанта | 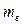 ,
т ,
т
| 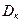 ,
м ,
м
| 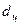 ,
м ,
м
| 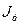 ,
кг*м ,
кг*м 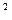
| 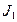 ,
кг*м ,
кг*м 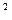
| 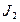 ,
кг*м ,
кг*м 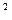
| 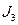 ,
кг*м ,
кг*м 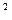
| 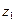
| 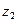
| 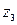
| 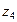
|
| 17 | 8,2 | 0,5 | 0,07 | 3,82 | 0,36 | 0,56 | 0,66 | 44 | 112 | 36 | 96 |
Таблиця 5
| Номер варіанта | 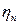
| 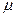
| 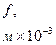
| 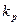
| 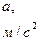
|
| 16 – 30 | 0,92 | 0,015 | 0,6 | 1,5 | 0,9 |
Розв’язок:
Нехтуючи податливістю механічних зв'язків, визначимо приведений до швидкості обертання двигуна статичний момент Мс
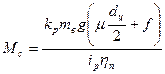 Н∙м.
Н∙м.
де: m в - спільна маса візка з вантажем;
d ц - діаметр цапф підшипників ходових колес;
z1, z2, z3 і z4 - числа зубців шестерень редуктора ;
ηп - ккд однієї шестеренної пари;
µ- коефіцієнт тертя в опорах ходових колес;
f - коефіцієнт тертя котіння ходових колес;
k - коефіцієнт що враховує тертя реборд колес об рейки;
i р - передаточне число редуктора.
Останнє дорівнює:
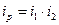 ,
,
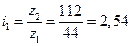 ,
,
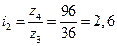 ,
,
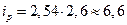 .
.
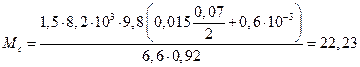 Н∙м.
Н∙м.
Знайдемо електромагнітний момент М двигуна та його динамічну складову Мдин в процесах сталого руху, розгону і гальмування:
M – Mc = J S∙∙ 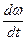 .
.
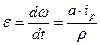
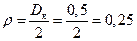 м.
м.
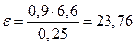
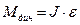
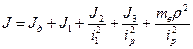
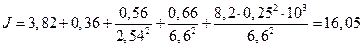 кг∙м2
кг∙м2
В процесах розгону і гальмування.
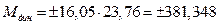 Н∙м.
Н∙м.
Знаки “+” і “-” відносяться відповідно до моментів:
Електромагнітний момент М двигуна в процесі сталого руху(Мдин=0)
M = Mc = 22,23 Н∙м.
Електромагнітний момент М двигуна в процесі, розгону (Мдин>0)
M = Mc + Мдин = 22,23+381,348=403,578 Н∙м.
Електромагнітний момент М в процесі гальмування (Мдин<0)
M = Mc - Мдин = 22,23-381,348=-359,118 Н∙м
Розрахункова кінематична схема електропривода у вигляді жорсткої (одномасової) системи та її структурна схема подані на рисунку 8.

Рисунок 8
Рівняння руху одномасової системи має вигляд:
M – Mc = J S∙∙p w .
Задача №5
На рис. 9 наведено кінематичну схему механічної частини електропривода повороту платформи 1 з технологічним обладнанням (наприклад, екскаватора або великовантажного маніпулятора), де 2 – двигун, 3 – з'єднувальна муфта, 4 – гальмо, 5 – редуктор; 6 – ведуча шестерня, 7 – нерухомий зубчастий венець, 8 - опорні ролики.
Знехтуючи податністю механічних зв'язків, визначити: допустимі значення моменту на валу двигуна при пуску і гальмуванні, момент утрат в передачі (редукторі та шестеренній парі "ведуча шестерня - зубчастий венець") і статичний момент в перехідних і усталеному режимах, якщо задані маса m п платформи з вантажем; діаметр Dк кола опорного роликового круга; діаметр d р роликів; момент інерції J д двигуна; момент інерції J 1 двигуна і жорстко зв'язаних з ним елементів (системи "ротор двигуна - редуктор - ведуча шестерня"); момент інерції J 2 поворотної платформи з розміщеним на неї вантажем (відносно вісі обертання платформи); допустиме лінійне прискорення aдоп платформи на колі її опорного роликового круга; коефіцієнт f тертя котіння роликів; коефіцієнт k р, що враховує тертя роликів опорного роликового круга об реборди спрямовуючої (на площині зубчастого венця) і тертя в центральній цапфі вісі обертання платформи; передатне число i р і ККД h р редуктора; передатне число i ш і ККД h ш шестеренній парі "ведуча шестерня - зубчастий венець".
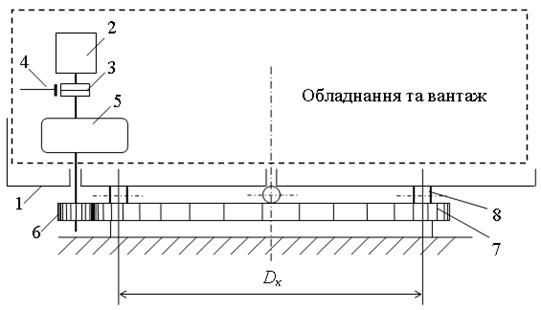
Рисунок 9
Таблиця 6
| Номер Варіанта | m п, т | D к, м | d р, м | J д, кг∙м2 | J 1, кг∙м2 | J 2, кг∙м2 | i р | i ш | a доп, м/с2 |
| 17 | 19 | 28 | 0,2 | 28,6 | 32,5 | 550 | 16 | 48 | 0,8 |
Таблиця 7
| Номер варіанта | ηр | ηш | f, м | k р |
| 16-30 | 0,9 | 0,92 | 0,0006 | 2,1 |
Розв’язок:
Нехтуючи податливістю механічних зв'язків, визначимо приведений до швидкості обертання двигуна статичний момент Мс
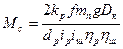 Н∙м.
Н∙м.
де: m п -маса платформи з вантажем; Dк - діаметр кола опорного роликового круга; d р – діаметр роликів; f - коефіцієнт тертя котіння роликів; k р - коефіцієнт, що враховує тертя роликів опорного роликового круга об реборди спрямовуючої (на площині зубчастого венця) і тертя в центральній цапфі вісі обертання платформи; i р передатне число і ККД h р редуктора; i ш - передатне число і ККД h ш шестеренній парі "ведуча шестерня - зубчастий венець".
Після підстановки даних :
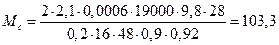 Н∙м
Н∙м
Знайдемо динамічну складову двигуна Мдин в процесах сталого руху, розгону і гальмування:
Мдин = J S∙∙ 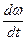 .
.
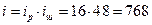
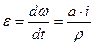
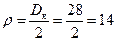 м.
м.
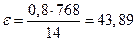
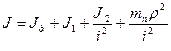
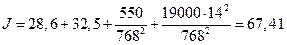 кг∙м2
кг∙м2
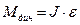
В процесах розгону і гальмування:
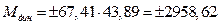 Н∙м.
Н∙м.
Знаки “+” і “-” відносяться відповідно до моментів:
Електромагнітний момент М двигуна в процесі, розгону (Мдин>0):
M = Mc + Мдин = 103,3+2958,62=3061,92 Н∙м.
Електромагнітний момент М в процесі гальмування (Мдин<0):
M = Mc - Мдин = 103,3-2958,62=-2855,32 Н∙м
Знайдемо момент втрат в передачі (на редукторі та шестернній парі "ведуча шестерня - зубчатий вінець"):
в процесі сталого руху і розгону:
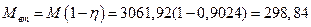 Н∙м
Н∙м
де - 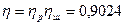
в процесі гальмування:
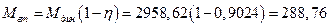 Н∙м.
Н∙м.
Знайдемо статичний момент в перехідному та установленому режимах.
Статичний момент в процесі сталого руху і розгону:
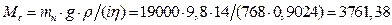 Н∙м.
Н∙м.
Статичний момент в процесі гальмування:
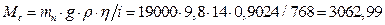 Н∙м.
Н∙м.
Задача №6
Механічні характеристики двигуна і статичного навантаження лінійні (див. рис.10, прямі 1 і 2). Отримайте аналітичні вирази функцій ω(t) і М(t) відповідно швидкості обертання і електромагнітного моменту двигуна для процеса пуску електропривода в часі (до усталеної швидкості ωуст), якщо задані M кз і M со - моменти двигуна і статичного навантаження при w = 0; b і b с - модулі жорсткості механічних характеристик двигуна і статичного навантаження; J - момент інерції електропривода, приведений до швидкості обертання двигуна. Графіки функцій ω(t) и М(t) проілюструйте рисунком. Обчисліть час пуску. Доведіть, що усталений режим буде стійким.
Рисунок 10 
Таблиця 8
| Номер варіанта | M кз, Н×м | M со, Н×м | b, Н·м·с | b с, Н·м·с | J, кг·м2 |
| 17 | 2050 | 210 | 13,67 | 0,85 | 8,6 |
Розв’язок:
Рівняння статичних механічних характеристик двигуна і навантаження мають вигляд:
M = M кз-b w;
M с = M со+b с w,
де M кз і M со - моменти двигуна і статичного навантаження при w=0; b і b с - модулі жорсткості цих характеристик.
M = 2050-13,67w;
M с = 210+0,85w,
Рівняння руху електропривода має вигляд:
М - Мс = J(d w/dt),
де J - момент інерції електропривода, приведений до швидкості обертання двигуна.
M кз - b w - M со - b с w = J(d w/dt).
Після перетворення отримуємо:
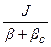 ×
× 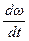 + w =
+ w = 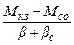 ,
,
або:
Тм(d w/dt) + w = w уст,
де Тм = J/(b + b c) - електромеханічна постійна часу електропривода,
wуст = (Mкз - Mсо)/(b + bс) – усталена швидкість (в точці перетину характеристик
1 і 2).
Тм = 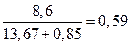 c
c
wуст = 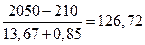 рад/с
рад/с
Рівняння руху електропривода:
0,59× 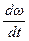 + w = 126,72
+ w = 126,72
Розв’язання неоднорідного диференційного рівняння має вигляд:
w ( t ) = A × 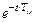 + w уст,
+ w уст,
де А - постійна інтегрування.
Постійна інтегрування А визначається із початкової умови: при t=0 швидкість дорівнює w(0)=w по ч =0. Після підстановки в значень t = 0 і w =w по ч=0 (в процесі пуску початкова швидкість дорівнює нулю) отримуємо:
А = w поч - w уст =0 – 126,72= -126,72.
В результаті підстановки отримуємо шуканий закон змінення швидкості в часі:
w ( t ) = А× 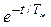 + w уст
+ w уст
w ( t ) = -126,72× 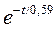 + 126,72
+ 126,72
Підставивши це рівняння у рівняння статичної механічної характеристики двигуна, отримуємо закон змінення електромагнітного момента двигуна в часі:
M ( t ) = M кз - b w ( t ) = M кз - b(w поч - w уст)× 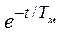 - b w уст
- b w уст
M ( t ) = 2050– 13,67w ( t ) = 2050 + 1732,26× 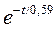 - 1732,26
- 1732,26
M ( t ) = 317,74 + 1732,26× 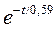 .
.
Усталене значення w уст і M уст відповідно швидкості і момента визначаються рішенням системи рівнянь статичних механічних характеристик двигуна і навантаження при М = Мс = Муст і w = w уст. Результат розв’язання: w уст = (M кз - M со)/(b + b с) = 65,29, як відмічалося вище, і Муст = M кз - b w уст = M кз - (M кз - M со)b/(b + b с).
Муст = 2050 - (2050 - 210) 13,67/(13,67 + 0,85) = 317,71 Н∙м
Якісні графіки залежностей ω( t ) і М( t ) наведені на рис. 11.
Піддотичні експонент w ( t ) і M ( t ) дорівнюють електромеханічній постійній часу Тм. Час перехідного процесу t пп, за якій швидкість змінюється від початкового значення w поч =0 до кінцевого w кін (або момент від початкового Мпоч до кінцевого Мкін), визначається з закону змінення електромагнітного момента двигуна в часі шляхом логаріфмування після підстановки w = w кін або М = Mкін:
t пп = Тм × ln[(wуст - w поч)/(wуст - wкін)] = Тм×ln[(M уст - Mпоч)/(Mуст - M кін)].
Приймаючи w кін = 0,95w уст або M кін = 0,95M уст, отримуємо оцінку часу перехідного процесу: t пп » 3Тм.
t пп =0,214 с
Примітка: отримання закону змінення електромагнітного момента двигуна в часі свідчить про те, що перехідні процеси в електроприводі при заданих статичних механічних характеристиках двигуна і статичного навантаження відносяться до категорії механічних перехідних процесів, оскільки завдання статичної механічної характеристики двигуна w ( M ) виявляється еквівалентним завданню функції М( t ). Закони змінення швидкості та моменту після закінчення перехідного процесу змінюються незначно (цими змінами можна принебрігати), тому робота двигуна буде стійкою.
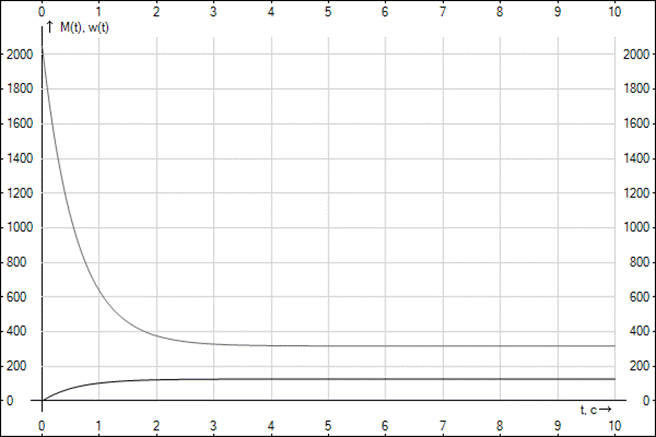
Рисунок 11
Задача №7
 Електропривод працює в усталеному режимі, що характеризується координатами точки А механічної характеристики 1 двигуна (рис.12), рівняння якої має вигляд ω = ω01 - М/β1. Двигун навантажений постійним за величиною реактивним статичним моментом Мс. Треба розрахувати і побудувати графіки ω(t) и М(t) змінення в часі швидкості обертання та електромагнітного моменту двигуна від початкових ω поч і Мпоч до кінцевих ω кін і Мкін значень в перехідному процесі, якій виникає при миттєвому переводі двигуна на механічну характеристику 2, рівняння якої має вигляд ω = ω 02 - М/β 2. Значення швидкостей ω 01 і ω 02 обертання двигуна при ідеальному холостому ході, модулей β 1 і β 2 жорсткості механічних характеристик 1 і 2, приведеного до валі двигуна підсумовного моменту інеції J електропривода та величини Мс статичного моменту наведені в табл.9.
Електропривод працює в усталеному режимі, що характеризується координатами точки А механічної характеристики 1 двигуна (рис.12), рівняння якої має вигляд ω = ω01 - М/β1. Двигун навантажений постійним за величиною реактивним статичним моментом Мс. Треба розрахувати і побудувати графіки ω(t) и М(t) змінення в часі швидкості обертання та електромагнітного моменту двигуна від початкових ω поч і Мпоч до кінцевих ω кін і Мкін значень в перехідному процесі, якій виникає при миттєвому переводі двигуна на механічну характеристику 2, рівняння якої має вигляд ω = ω 02 - М/β 2. Значення швидкостей ω 01 і ω 02 обертання двигуна при ідеальному холостому ході, модулей β 1 і β 2 жорсткості механічних характеристик 1 і 2, приведеного до валі двигуна підсумовного моменту інеції J електропривода та величини Мс статичного моменту наведені в табл.9.
Таблиця 9
| Номер варіанта | ω 01, рад/с | b 1, Н·м·с | ω 02, рад/с | b 2, Н·м·с | M с, Н×м | J, кг·м2 |
| 17 | 104,66 | 7,64 | 0 | 1,8 | 150 | 10,0 |
Розв’язок:
Рівняння статичної механічної характеристики двигуна
ω = ω0 - М/β,
де β - модуль жорсткості цієї характеристики.
Початкову швидкість знайдемо з закону змінення першого графіку. В сталому режимі електромагнітний момент дорівнює статичному (М = Мс):
ω поч = ω 01 - Мс/β 1 = 104,66 - 150/7,64 = 85 рад/с.
Знаходимо швидкість усталеного режиму на другому графіку:
ω уст = ω 02 - Мс/β 2 = 0 - 150/1,8 = -83,3 рад/с.
При Мс = Const електромеханічна постійна часу електропривода:
Тм = J/β 1 = 10/7,64 = 1,31 c.
Момент короткого замикання:
Мкз = β 1 ω 01 = 7,64×104,66 = 799,6 Н×м.
Функція ω ( t ) є рішенням диференційного рівняння:
Тм(d ω/dt) + ω = ω уст.
У процесі розгону двигуна із непорушного стану до усталеної швидкості при ω 0 = Const рішення рівняння (2.59) має вигляд:
ω = ωпоч 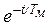 + ω уст(1 -
+ ω уст(1 - 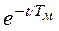 ).
).
ω( t ) = 85 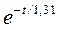 - 83,3(1 -
- 83,3(1 - 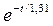 ) рад/с.
) рад/с.
Закон змінення електромагнітного моменту в часі:
М( t ) = Мкз – β 2 ω ( t ) = Мкз – β 2 ω поч 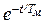 + β 2 ω уст(1 -
+ β 2 ω уст(1 - 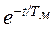 )
)
М( t ) = 799, 6 – 153 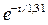 - 149,94 (1 -
- 149,94 (1 - 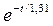 ) Н·м.
) Н·м. 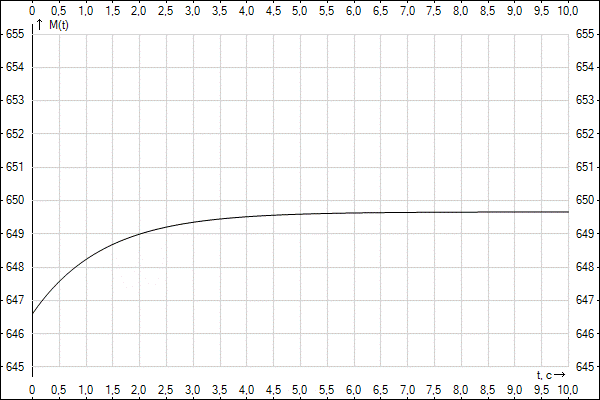
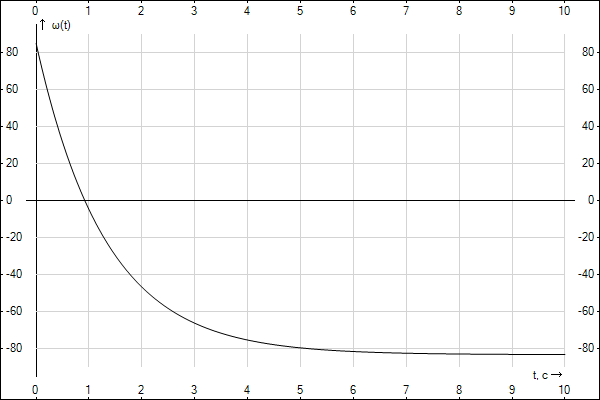
Рисунок 13, 14
Задача №8
Електромагнітний момент електродвигуна змінюється в часі за законом:
М(t) = a + bt. Статичний момент Мс постійний за величиною, реактивний, не перешкоджуючий руху в позитивному напрямку. Визначити закон w(t) змінення кутової швидкості обертання двигуна та побудувати графік функції w(t), якщо початкове значення швидкості wпоч = 0. Поясніть, за яких умов перехідний процес може бути перерваний з переходом в усталений режим.
Значення моменту інерції J механічної частини електропривода, приведеного до швидкості обертання двигуна, величини Мс статичного моменту, коефіцієнтів a, b та постійної часу Т наведені в табл.10.
Таблиця 10
| Номер варіанта | J, кг·м2 | M с, Н×м | a, Н×м | b, Н·м | T, с |
| 17 | 2,8 | 240 | -380 | 750 | 0,01 |
Розв’язок:
Закон зміни моменту двигуна у часі має вигляд:
М( t) = а + b(1- et/ T) = -380-750(1-е t/0,01 )
Рівняння руху електропривода для додатного напрямку руху має вид:
| |
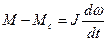 ,
,
або
| |
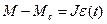 .
.
Звідси кутове прискорення буде:
| |
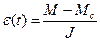 .
.
Підставимо в заданий закон змінення в часі електромагнітного моменту двигуна. Тоді отримаємо:
| |
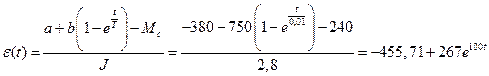 .
.
Проінтегрувавши вираз 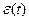 , отримаємо шуканий закон ω(t) змінення кутової швидкості обертання двигуна (з урахуванням, що за умовою задачі ωпоч = 0):
, отримаємо шуканий закон ω(t) змінення кутової швидкості обертання двигуна (з урахуванням, що за умовою задачі ωпоч = 0):
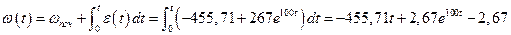 .
.
За отриманою залежністю побудуємо графік швидкості обертання двигуна від часу ω(t).
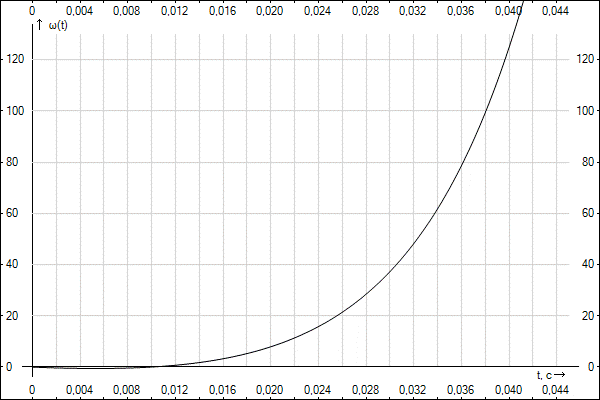
Рисунок 15
В початковий момент пуску електропривода пусковий момент перевищує статичний момент, тому пуск двигуна відбувається відразу. Перехідний процес може бути перерваний з переходом в усталений режим за умови, якщо початковий момент двигуна буде меншим, за статичний. Продовж інтервалу часу, коли зберігається співвідношення 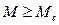 двигун буде розганятися. Цей інтервал називається часом пуску.
двигун буде розганятися. Цей інтервал називається часом пуску.
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1.Методичні вказівки до самостійної роботи з дисципліни «Автоматизований електропривод» (Частина 1. Загальні питання автоматизованого електропривода) Суми, видавництво СумДУ 2004.
2. Методичні вказівки до самостійної роботи з дисципліни «Автоматизований електропривод» (Частина 2. Механіка електропривода) Суми, видавництво СумДУ 2006.








