Архангельский государственный технический университет
Министерство образования и науки Российской Федерации
Архангельский государственный технический университет
ЭЛЕКТРОДИНАМИКА
Методические указания
к выполнению контрольного задания № 3
для студентов-заочников
инженерно-технических специальностей
Архангельск
2004
Рассмотрены и рекомендованы к изданию методической комиссией
факультета промышленной энергетики
Архангельского государственного технического университета
29 октября 2003 г.
Составители:
Л.В. Филимоненкова, доц., канд. техн. наук;
Н.С. Самылова, ст. преп.;
И.В. Шульгин,ст. преп.
Рецензент
А.В.Соловьев, доц.,канд. техн. наук
УДК 530.1
Филимоненкова Л.В., Самылова Н.С., Шульгин И.В. Электродинамика: Методические указания к выполнению контрольного задания N3 для студентов-заочников инженерно-технических специальностей Архангельск: Изд-во АГТУ, 2004. – 45 с.
Подготовлены кафедрой физики АГТУ.
В указаниях даны общие рекомендации к решению задач по электромагнетизму, приведен необходимый справочный материал.
Предназначены для студентов-заочников инженерно-технических специальностей.
Ил. 35. Табл. 4. Библиогр. 8 назв.
ã Архангельский государственный технический университет , 2004
РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
К выполнению контрольной работы следует приступить только после изучения материала, соответствующего данному разделу программы, внимательного ознакомления с примерами решения задач, приведенных в данном пособии по каждому разделу курса.
При выполнении контрольной работы необходимо руководствоваться следующими правилами.
1. Контрольная работа выполняется в обычной школьной тетради (каждая контрольная выполняется в отдельной тетради). Для замечаний рецензента на страницах тетради оставляются поля. Каждая следующая задача должна начинаться с новой страницы. Условия задач переписываются полностью без сокращений.
2. При решении задач следует пользоваться международной системой единиц ( СИ ). Все величины, входящие в условия задачи, выражаются в единицах этой системы.
3. Решения задач должны сопровождаться краткими, но исчерпывающими пояснениями, раскрывающими физический смысл употребляемых формул. В тех случаях, когда это возможно, дать чертеж, выполненный с помощью чертежных принадлежностей.
Если при решении задачи применяется формула, получаемая для частного случая, не выражающая какой-нибудь физический закон или не являющаяся определением какой-нибудь физической величины, то её следует вывести.
4. Решать задачу надо в общем виде, то есть выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. При таком способе решения не производятся вычисления промежуточных величин.
Получив решение в общем виде, сделать анализ его размерности. Для этого надо подставить в правую часть полученной рабочей формулы вместо символов величин обозначения единиц, провести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине. Если такого соответствия нет, то это означает, что задача решена неверно.
5. В конце контрольной работы следует указать учебники и учебные пособия, которыми пользовались при решении задач.
6. Получив из университета проверенную работу, следует внимательно ознакомиться с замечаниями и указаниями рецензента. Если при выполнении контрольной работы были допущены ошибки, необходимо выполнить работу над ошибками в той же тетради и направить ее на повторную проверку.
7. После получения положительной рецензии студент обязан пройти собеседование по существу решенных задач. Итогом собеседования является зачет по контрольной работе.
8. Студентам, проживающим вблизи университета или филиалов и учебно – консультационных пунктов, рекомендуется прослушать курс лекции по физике, организуемых для студентов заочников, а также использовать очные консультации преподавателей кафедры физики.
Основные уравнения электродинамики
1. Электростатика
1.1. Закон сохранения электрического заряда:
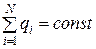 ,
,
где 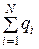 - алгебраическая сумма зарядов, входящих в изолированную систему; N - число зарядов.
- алгебраическая сумма зарядов, входящих в изолированную систему; N - число зарядов.
1.2. Закон Кулона. Сила взаимодействия 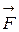 между двумя точечными зарядами и модуль этой силы F:
между двумя точечными зарядами и модуль этой силы F:
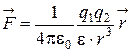 ;
; 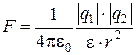 ,
,
где 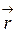 - радиус-вектор, соединяющий заряды;
- радиус-вектор, соединяющий заряды; 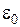 - электрическая постоянная,
- электрическая постоянная, 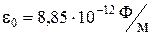 , e - диэлектрическая проницаемость среды, в которой расположены заряды q1 , q2.
, e - диэлектрическая проницаемость среды, в которой расположены заряды q1 , q2.
Здесь коэффициент:
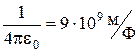 .
.
1.3. Характеристики электрического поля:
напряженность 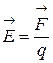 ; потенциал
; потенциал 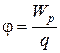 ,
,
где 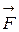 - сила, действующая на точечный положительный заряд q, помещенный в данную точку поля,
- сила, действующая на точечный положительный заряд q, помещенный в данную точку поля, 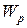 -потенциальная энергия точечного положительного заряда q, помещенного в данную точку поля.
-потенциальная энергия точечного положительного заряда q, помещенного в данную точку поля.
1.4. Напряженность 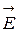 и потенциал j поля точечного заряда q:
и потенциал j поля точечного заряда q:
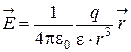 ;
; 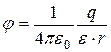 ,
,
где 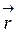 - радиус - вектор, проведенный из точки, в которой расположен заряд q, до интересующей нас точки.
- радиус - вектор, проведенный из точки, в которой расположен заряд q, до интересующей нас точки.
1.5. Напряженность и потенциал электрического поля, создаваемого заряженной сферической поверхностью радиусом R, несущей заряд q, на расстоянии r от центра сферы:
· внутри сферы (r < R)
E=0; 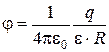 ;
;
· на поверхности сферы (r = R)
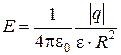 ;
; 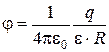 ;
;
· вне сферы (r > R)
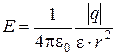 ;
; 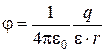 .
. 
1.6. Распределение зарядов. Для упрощения математических расчетов во многих случаях бывает удобно игнорировать тот факт, что заряды имеют дискретную структуру и считать, что они “размазаны” определенным образом в пространстве. Другими словами, удобно заменить истинное распределение точечных дискретных зарядов фиктивным непрерывным распределением. При переходе к непрерывному распределению вводят понятие о плотности заряда — объемной r, поверхностной s, линейной t:
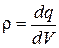 ,
, 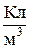 ;
; 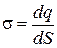 ,
, 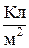 ;
; 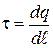 ,
, 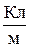 ,
,
где dq – заряд, заключенный в объеме dV , на поверхности dS, на длине dl.
1.7. Напряженность электрического поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) на расстоянии r от его оси:
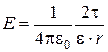 ,
,
где t-линейная плотность заряда.
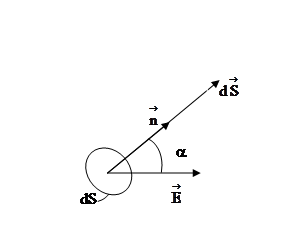
1.8. Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью:
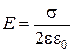 ,
,
где s – поверхностная плотность заряда.
1.9. Поток ФЕ вектора напряженности 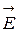 электрического поля:
электрического поля:
· через плоскую поверхность, помещенную в однородное поле,
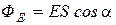 ,
,
· через произвольную поверхность S, помещенную в неоднородное поле,
|
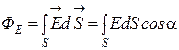 ,
,
где 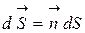 вектор, модуль которого равен dS, а напрвление совпадает с направлением единичного вектора нормали
вектор, модуль которого равен dS, а напрвление совпадает с направлением единичного вектора нормали 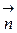 к элементу поверхности; a - угол между вектором напряженности
к элементу поверхности; a - угол между вектором напряженности 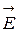 и нормалью
и нормалью 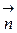 к элементу поверхности (рис.1).
к элементу поверхности (рис.1).
1.10. Теорема Остроградского-Гаусса. Поток вектора напряженности 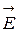 через любую замкнутую поверхность, охватывающую заряды q 1 , q 2 ,…, qN:
через любую замкнутую поверхность, охватывающую заряды q 1 , q 2 ,…, qN:
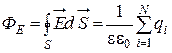 ,
,
где 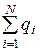 - алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; N-число зарядов.
- алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; N-число зарядов.
1.11. Cвязь между напряженностью и потенциалом:
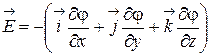 или
или 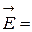 - gradj ,
- gradj ,
где 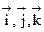 - единичные векторы координатных осей x,y,z.
- единичные векторы координатных осей x,y,z.
Знак минус показывает ,что вектор 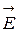 направлен в сторону убывания потенциала.
направлен в сторону убывания потенциала.
В случае электрического поля, обладающего сферической симметрией, эта связь выражается:
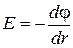 ;
; 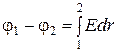 .
.
В случае однородного поля:
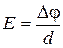 ;
; 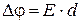 ,
,
где Dj=(j1- j2) - разность потенциалов двух точек поля вдоль силовой линии; d-расстояние между этими точками.
1.12. Принцип суперпозиции (наложения) электрических полей:
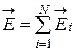 ;
; 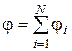 ,
,
где 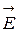 - напряженность результирующего поля, созданного несколькими точечными зарядами, равная векторной сумме напряженностей складываемых полей;
- напряженность результирующего поля, созданного несколькими точечными зарядами, равная векторной сумме напряженностей складываемых полей;
j - потенциал поля, созданного системой N точечных зарядов, равный алгебраической сумме потенциалов, создаваемых отдельными точечными зарядами.
1.13. Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал j1, в другую, имеющую потенциал j2:
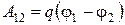 .
.
1.14. Энергия взаимодействия системы точечных зарядов:
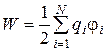 ,
,
где ji - потенциал, создаваемый в той точке, в которой находится заряд q i, всеми зарядами, кроме i-го.
1.15. Электроемкость конденсатора:
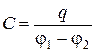 ,
,
где q - заряд , накопленный на конденсаторе, 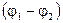 - разность потенциалов между обкладками.
- разность потенциалов между обкладками.
1.16. Электроемкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью e:
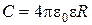 ,
,
где S - площадь пластин; d - расстояние между пластинами; e - диэлектричес-кая проницаемость диэлектрика, заполняющего пространство между пластинами.
1.17. Соединение конденсаторов в батареи.
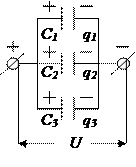
| Соединение | Параллельное | Последовательное |
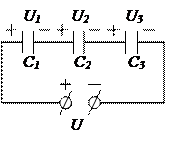 Схема Схема
| 
| |
| Сохраняющаяся величена | U1=U2=U3=Un=const | q1=q2=q3=qn=const |
| Суммируемые величины | 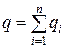
| 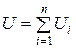
|
| Результирующая емкость | 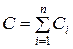
| 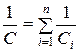
|
1.18. Энергия заряженного конденсатора:
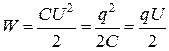 ,
,
где q - заряд конденсатора; C- электроемкость; U- разность потенциалов между обкладками.
1.19. Пондеромоторная сила - сила, с которой пластины конденсатора притягивают друг друга:
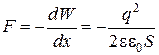 ,
,
где знак минус указывает, что сила F- сила притяжения.
1.20. Объемная плотность энергии:
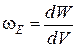 .
.
В случае однородного поля, то есть поля, напряженность которого в каждой точке его одинакова как по модулю, так и по направлению ( 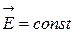 ):
):
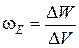 .
.
Для электрического поля в среде с диэлектрической проницаемостью e плотность энергии через напряженность поля Е:
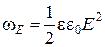 .
.
1.21. Полная энергия электрического поля через объемную плотность энергии:
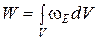 .
.
 Примеры решения задач
Примеры решения задач
Пример 1.
|
Три точечных заряда q1= q2= q3=1нКл расположены в вершинах равно-стороннего треугольника. Какой заряд q 4 нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии?
Дано: q1= q2= q3=1 нКл=10-9 Кл
Найти: q4.
Решение.
Все три заряда, расположенные по вершинам треугольника, находятся в одинаковых условиях. Поэтому достаточно выяснить, какой заряд следует поместить в центре треугольника, чтобы какой – нибудь один из трех зарядов, например q1, находился в равновесии.
Заряд q1 будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю (рис. 2):
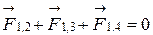 , (1)
, (1)
где 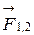 ,
, 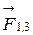 ,
, 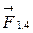 -силы, с которыми действуют на заряд q1 заряды q2, q3, q4.
-силы, с которыми действуют на заряд q1 заряды q2, q3, q4.
Заменим векторное равенство (1) скалярным соотношением в проекции на ось x. Учитывая расположение зарядов, выберем ось x, проходящую через заряды q1 и q4, то есть совпадающую с биссектрисой угла равностороннего треугольника:
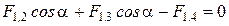 .
.
Учитывая, что F1,2=F1,3, получим:
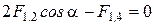 .
.
Применяя закон Кулона и имея в виду, что q1=q2=q3, получим:
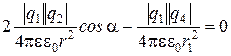
или
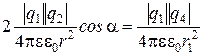 .
.
Выполнив преобразования, найдем
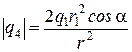 . (2)
. (2)
Из геометрических построений в равностороннем треугольнике следует:
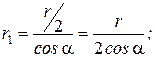
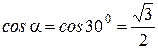 .
.
C учетом этого формула (2) примет вид:
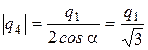 .
.
Подставив численные значения, получим
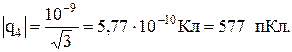
q 4= - 577 пКл.
Следует отметить, что равновесие системы зарядов будет неустойчивым.
Пример 2.
Электрическое поле создано двумя точечными зарядами q1=30 нКл и q2= -10 нКл. Расстояние между двумя зарядами d=20 см. Определить напряженность электрического поля в точке, находящейся на расстоянии r1=15 см от первого заряда, на расстоянии r2=10 см от второго заряда (рис.3).
Дано: q1=30 нКл =30×10-9 Кл, q2=-10 нКл =-10×10-9 Кл, d=20 см =20×10-2 м, r1=15 см =15×10-2 м, r2=10 см =10×10-2 м.
Найти: Е.
Решение.
Согласно принципу суперпозиции электрических полей каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность 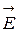 электрического поля в искомой точке может быть найдена как векторная сумма напряженностей
электрического поля в искомой точке может быть найдена как векторная сумма напряженностей 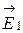 и
и 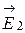 полей, создаваемых каждым зарядом в отдельности:
полей, создаваемых каждым зарядом в отдельности:
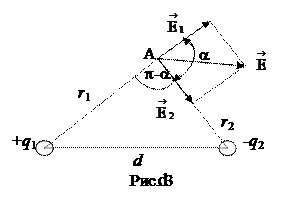
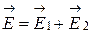 .
.
Напряженность электрического поля, создаваемого в вакууме (e=1) первым зарядом q1:
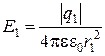 ,
,
вторым зарядом q2:
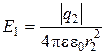 .
.
Вектор 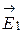 (рис.3) направлен по силовой линии от заряда q1, так как заряд q1 положителен; вектор
(рис.3) направлен по силовой линии от заряда q1, так как заряд q1 положителен; вектор 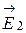 направлен так же по силовой линии, но к заряду q2, так как заряд q2 отрицателен.
направлен так же по силовой линии, но к заряду q2, так как заряд q2 отрицателен.
Абсолютное значение вектора 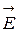 найдем, используя теорему косинусов:
найдем, используя теорему косинусов:
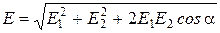 , (3)
, (3)
где a - угол между векторами 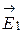 и
и  может быть найден из треугольника со сторонами r 1 , r 2 и d ,
может быть найден из треугольника со сторонами r 1 , r 2 и d ,
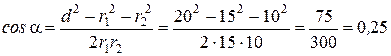 .
.
Производя подстановку в уравнение (3) и вынося общий множитель 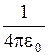 за знак корня, получим:
за знак корня, получим:
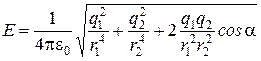 .
.
Подставив численные значения, получим:
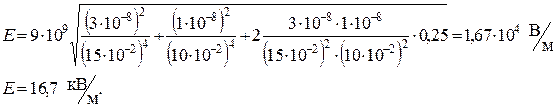
Пример 3.
Тонкое кольцо радиусом R=8 см несет заряд, равномерно распределенный с линейной плотностью t=10-8 Кл/м. Какова напряженность электричес-кого поля в точке, равноудаленной от всех точек кольца на расстояние r=10 см?
Дано: R=8 см =8×10-2 м, t=10-8 Кл/м, r=10 см =10×10-2 м.
Найти E.
 Решение.
Решение.
|
Поле создано зарядом, распределенным по тонко-му кольцу заданного ради-уса. Оно не обладает дос-таточной симметрией даже при равномерном распре-делении заряда (нельзя указать точную конфигу-рацию силовых линий), поэтому для расчета на-пряженности можно ис-пользовать только прин-цип суперпозиции 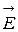 .
.
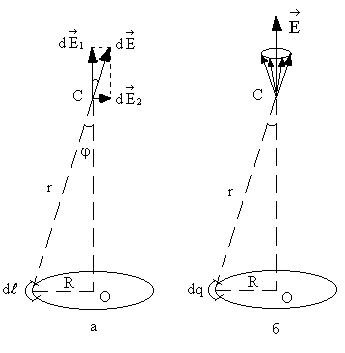
Разобьем кольцо на элемен-тарные участки dl (рис.4,а).
Каждый такой участок можно принять за точечный заряд, несущий заряд dq=tdl. Элементарный заряд dq, находящийся на элементе dl, создает в данной точке С на расстоянии r вектор напряженности 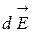 , равный по модулю:
, равный по модулю:
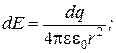
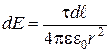 ,
,
где r- расстояние от элемента заряда dq до точки поля С.
Векторы 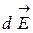 от всех элементарных участков образуют симметричный конический веер (рис.4,б). Из соображений симметрии можно заключить, что результирующий вектор
от всех элементарных участков образуют симметричный конический веер (рис.4,б). Из соображений симметрии можно заключить, что результирующий вектор 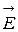 направлен вдоль оси кольца. Каждый из составляющих векторов
направлен вдоль оси кольца. Каждый из составляющих векторов 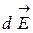 вносит в результирующий вектор вклад
вносит в результирующий вектор вклад 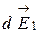 , равный по модулю:
, равный по модулю:
d Е1= d Е cosj
или
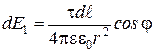 , (4)
, (4)
при этом составляющие 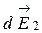 , параллельные плоскости кольца, в сумме дают нуль. Проинтегрировав по всему кольцу уравнение (4) и заменив cosj через r и R (
, параллельные плоскости кольца, в сумме дают нуль. Проинтегрировав по всему кольцу уравнение (4) и заменив cosj через r и R ( 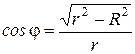 ), получим абсолютное значение результирующего вектора
), получим абсолютное значение результирующего вектора 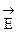 :
:
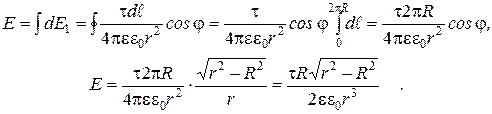
Подставив численные значения, получим:
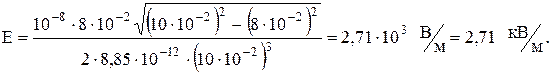 .
.
Пример 4.
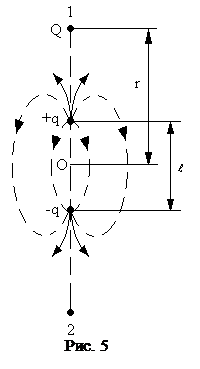
Точечный заряд Q=-2×10-10 Кл расположен на продолжении оси диполя, электрический момент которого Pq=1,5×10-10 Кл×м , на расстоя-нии r=10 см от центра (ближе к положи-тельному заряду диполя). Какую работу надо совершить, чтобы перенести этот заряд в симметрично расположенную точку по другую сторону диполя? Плечо диполя l << r (рис. 5).
Дано: Q=-2×10-10 Кл, Р q=1,5×10-10 Кл×м, r=10 см =10×10-2 м, l << r .
Найти: А.
Решение.
Работа А*, совершаемая внешними силами при перемещении заряда в электрическом поле, равна работе сил поля, взятой с обратным знаком:
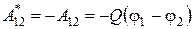 , (5)
, (5)
где j1, j2 – потенциалы соответственно начальной и конечной точек.
Поле создается двумя точечными зарядами + q и – q диполя, и потенциалы точек 1 и 2 следует искать методом суперпозиции. Как видно из рисунка 5, точка 1 находиться на расстоянии 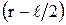 от положительного заряда и на расстоянии
от положительного заряда и на расстоянии 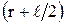 от отрицательного заряда. В соответствии с этим потенциал первой точки:
от отрицательного заряда. В соответствии с этим потенциал первой точки:
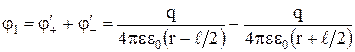 , (6)
, (6)
где 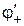 ,
, 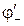 – потенциалы в первой точке, созданные соответственно положительным и отрицательным зарядами:
– потенциалы в первой точке, созданные соответственно положительным и отрицательным зарядами:
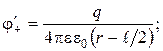
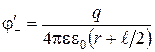
Аналогично потенциал второй точки:
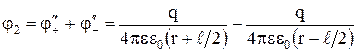 . (7)
. (7)
Приведем к общему знаменателю каждое из выражений (6) и (7):
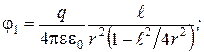 (8)
(8)
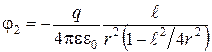 . (9)
. (9)
Если учесть, что ql = Pq и при r >>l членами 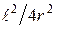 можно пренебречь, то выражения (8) и (9) примут вид:
можно пренебречь, то выражения (8) и (9) примут вид:
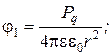
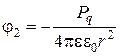
Подставив эти выражения в уравнении (5), получим:
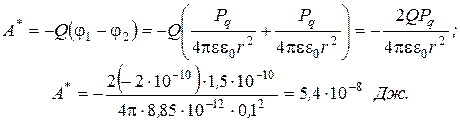
Пример 5
Электрическое поле создано длинным цилиндром радиусом R=1 см, равномерно заряженным с линейной плотностью t=20 нКл./м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии а1=0,5 см и а2=2 см от поверхности цилиндра в средней его части (рис. 6).
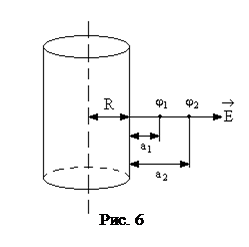 Дано: R=1 см =10-2 м, t=20 нКл/м =20×10-9 Кл/м, а1=0,5 см =5×10-3 м, а2=2 см =2×10-2 м.
Дано: R=1 см =10-2 м, t=20 нКл/м =20×10-9 Кл/м, а1=0,5 см =5×10-3 м, а2=2 см =2×10-2 м.
Найти: Dj.
Решение.
Для определения разности потенциалов воспользуемся соотношением между напряженностью поля и изменением потенциала:
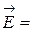 -qradj .
-qradj .
Для поля с осевой симметрией, каким является поле цилиндра, это соотно-шение можно записать в виде:
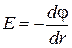 или
или 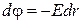 .
.
Проинтегрировав это выражение, найдем разность потенциалов двух точек, отстоящих на расстояниях r1 и r2 от оси цилиндра:
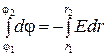 или
или 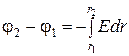 . (10)
. (10)
Так как цилиндр и точки взяты вблизи его средней части, то для выражения напряженности поля можно воспользоваться формулой напряженности поля, созданного бесконечно длинным цилиндром:
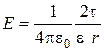 .
.
Произведя подстановку в уравнение (10), получим:
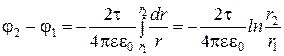
или
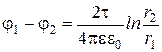 . (11)
. (11)
Так как величины r 1 и r 2 входят в формулу (11) в виде отношения, то их можно выразить в любых, но только одинаковых единицах:
r1=R+a1=1,5 см; r2=R+a2=3 см
Подставим численные значения в формулу 11, получим:
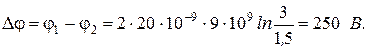
2. Электрический ток
2.1 Сила тока есть скалярная физическая величена, определяемая зарядом, проходящем через поперечное сечение проводника в единицу времени:
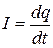 .
.
2.2. Постоянный ток – ток, сила тока и направление которого не изменяется со временем:
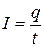 ,
,
где q – заряд, прошедший через поперечное сечение проводника за время t.
2.3. Плотность тока есть величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока:
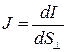 .
.
2.4. Сопротивление однородного проводника:
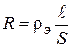 ,
,
где rэ - удельное сопротивление вещества проводника; 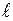 - его длина; S- площадь поперечного сечения.
- его длина; S- площадь поперечного сечения.
 |
2.5. Закон Ома
· для неоднородного участка цепи:
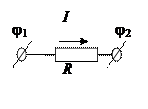
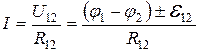 ,
,
· для однородного участка цепи ( 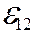 =0):
=0):

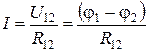 ,
,
· для замкнутой цепи:
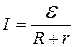 ,
,
где 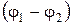 - разность потенциалов на концах участка цепи;
- разность потенциалов на концах участка цепи; 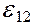 - ЭДС источников тока, входящих в участок; U12 - падение напряжения на участке цепи; R12 - сопротивление участка цепи; R - сопротивление внешней цепи; r - внутреннее сопротивление источника тока;
- ЭДС источников тока, входящих в участок; U12 - падение напряжения на участке цепи; R12 - сопротивление участка цепи; R - сопротивление внешней цепи; r - внутреннее сопротивление источника тока; 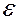 - ЭДС всех источников тока цепи.
- ЭДС всех источников тока цепи.
2.6. Работа постоянного тока на участке за время t:
A = IUt.
2.7. Мощность тока PR при прохождении тока по участку с сопротивлением R:
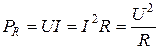 .
.
2.8. Полная мощность цепи - мощность, развиваемая источником тока:
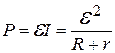 .
.
2.9. Коэффициент полезного действия источника тока:
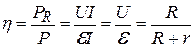 .
.
2.10. Закон Джоуля - Ленца. Если ток проходит по неподвижному проводнику, то вся работа идет на его нагревание и количество теплоты, выделяющееся в участке цепи за время dt:
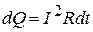 .
.
В случае постоянного тока (I=const):
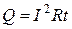 .
.
2.11. Законы Кирхгофа.
Первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю; т. е.
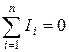 ,
,
где n– число токов, сходящихся в узле.
Второй закон Кирхгофа: в любом замкнутом контуре разветвленной цепи алгебраическая сумма произведений сил токов Ii на сопротивление Ri соответствующих участков этого контура равна алгебраической сумме ЭДС 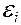 , встречающихся в этом контуре; т. е.
, встречающихся в этом контуре; т. е.
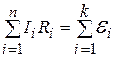
где n- число участков, содержащих активное сопротивление; к - число источников в контуре.
При решении задач по законам Кирхгофа надо придерживаться следующих правил.
1. Обозначить на схеме буквами узлы и контуры.
2. Произвольно выбрать направление токов (если они не оговорены условием задачи) во всех участках цепи и обозначить их на чертеже стрелками.
3. Учесть направление токов при составлении первого закона. Положи-тельными считать токи, подходящие к узлу, а отрицательными – отходя-щие от узла.
4.  Составить систему уравнений для первого закона Кирхгофа. Число уравнений, составленных по этому закону, должно быть на единицу меньше числа узлов в цепи.
Составить систему уравнений для первого закона Кирхгофа. Число уравнений, составленных по этому закону, должно быть на единицу меньше числа узлов в цепи.
5.  Выбрать произвольно направление обхода контуров. Условиться, что ЭДС в уравнении будет положи-тельной, если направление от отрицательного полюса к положительному совпадает с направлением обхода, в противном случае ЭДС следует считать отрицательной.
Выбрать произвольно направление обхода контуров. Условиться, что ЭДС в уравнении будет положи-тельной, если направление от отрицательного полюса к положительному совпадает с направлением обхода, в противном случае ЭДС следует считать отрицательной.
6. Считать падение напряжения в цепи (IR) положи-тельным, если выбранное ранее направление тока на этом участке (между двумя узлами) совпадает с направлением обхода контура, и отрица-тельным, если направление тока не совпадает с направлением обхода контура.
7. Первый контур выбрать произвольно. При составлении уравнений следующих контуров надо включать в них контуры, ранее не входящие.
8. Число уравнений, составленных по второму закону Кирхгофа, определяется следующими условиями. Если число контуров в цепи m, а узлов в ней n, то число независимых уравнений, достаточных для решения, будет равно m-n+1.
9. Получение в ответе токов с отрицательными знаками означает, что было выбрано направление, обратное действительному.
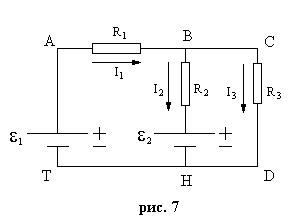
Пример 6
Найти токи, протекающие в каждой ветви электрической цепи (рис. 7), если 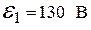 ,
, 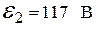 R 1=0,5 Ом, R 2=0,3 Ом, R 3=120 Ом. Внутреннее сопротивление источника тока не учитывать.
R 1=0,5 Ом, R 2=0,3 Ом, R 3=120 Ом. Внутреннее сопротивление источника тока не учитывать.
Дано: 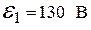 ,
, 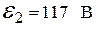 , R 1=0,5 Ом, R 2=0,3 Ом, R 3=120 Ом.
, R 1=0,5 Ом, R 2=0,3 Ом, R 3=120 Ом.
Найти: I1, I2, I3.
Решение.
 Задача дана для расчета разветвленных цепей, когда в них есть несколько источников тока. При решении задач такого типа рационально пользоваться законами Кирхгофа.
Задача дана для расчета разветвленных цепей, когда в них есть несколько источников тока. При решении задач такого типа рационально пользоваться законами Кирхгофа.
1. Обозначаем на схеме (рис. 7) контуры, узлы и направление токов.
2. Устанавливаем число ветвей m (в данной схеме их три) и число узлов n (в данной схеме их два - в точках В и Н).
3.
|
Для составления уравнений по первому закону Кирхгофа достаточно выбрать один из указанных узлов. Выберем узел В, в котором сходятся токи от трех проводников. Учитывая направления токов, получим:
I1-I2-I3=0. (12)
4. Устанавливаем число уравнений, необходимых для решения задач по второму закону Кирхгофа. Это число уравнений равно m - n+I=3-2+I=2. Выбираем контуры ВСДНВ и АВНТА.
5. Устанавливаем обход по контуру ВСДНВ, учитывая правило знаков при обходе тока внутри источников ЭДС. Выбираем обход по часовой стрелке, при котором ЭДС 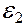 будет положительной. С учетом выбранного ранее направления токов составляем первое уравнение по второму закону Кирхгофа:
будет положительной. С учетом выбранного ранее направления токов составляем первое уравнение по второму закону Кирхгофа:
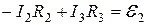 (13)
(13)
Cоставляем уравнение для второго контура BHTAB. Так как в этом контуре два источника тока ( 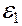 >
> 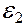 ), обход начинаем от
), обход начинаем от 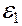 к
к 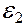 по часовой стрелке.
по часовой стрелке.
Кроме того, знаки при ЭДС и падения напряжения IR устанавливаем в соответствии с ранее приведенными правилами:
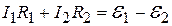 (14)
(14)
Подставив в равенства (12), (13), (14) значения сопротивлений и ЭДС, получим систему уравнений:
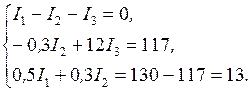
Эту систему уравнений с тремя неизвестными можно решить обычными приемами алгебры, в данной задаче удобно воспользоваться методом определителей (детерминантов). С этой целью перепишем уравнения еще раз в следующем виде:
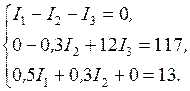
Искомые значения токов найдем из выражений:
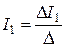 ;
; 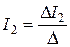 ;
; 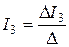 ,
,
где D - определитель системы уравнений; 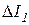 ,
, 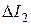 ,
, 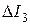 - определители, полученные заменой соответствующих столбцов определителя D столбцами, составленными из свободных членов трех вышеприведенных уравнений.
- определители, полученные заменой соответствующих столбцов определителя D столбцами, составленными из свободных членов трех вышеприведенных уравнений.
Составим и вычислим определитель системы и определители для I 1 , I 2 , I 3:
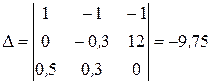 ;
; 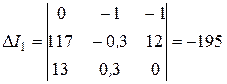 ;
;
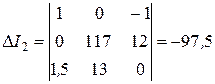 ;
; 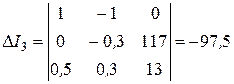 .
.
Отсюда получаем:
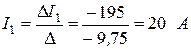 ;
;
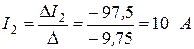 ;
;
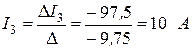 .
.
3. Магнитное поле тока
3.1 Характеристики магнитного поля:
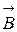 - вектор магнитной индукции – характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками;
- вектор магнитной индукции – характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками;
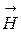 - вектор напряженности – характеризует магнитное поле, создаваемое только макротоками.
- вектор напряженности – характеризует магнитное поле, создаваемое только макротоками.
В случае однородной изотропной среды:
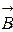 =
= 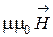 ,
,
где 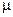 - магнитная проницаемость среды;
- магнитная проницаемость среды; 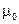 - магнитная постоянная,
- магнитная постоянная, 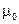 =4p×10-7Гн/м.
=4p×10-7Гн/м.
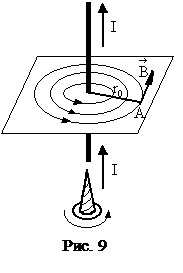
3.2 Закон Био-Савара-Лапласа. Элемент проводника 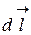 с током I создает в некоторой точке А индукцию поля:
с током I создает в некоторой точке А индукцию поля:
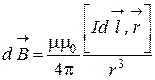 ;
; 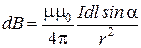 ,
,
где - 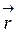 - радиус-вектор, проведенный из элемента
- радиус-вектор, проведенный из элемента 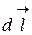 проводника в точку А; a – угол между радиусом-вектором и направлением тока в элементе проводника (рис. 8).
проводника в точку А; a – угол между радиусом-вектором и направлением тока в элементе проводника (рис. 8).
 |
3.3 Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током:
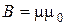
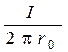 ,
,
где 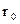 - кратчайшее расстояние от оси проводника до точки, в которой определяется магнитная индукция.
- кратчайшее расстояние от оси проводника до точки, в которой определяется магнитная индукция.
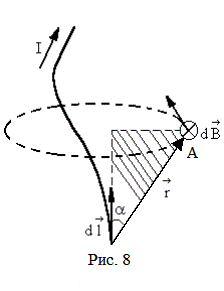
Вектор индукции 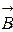 направлен по касательной к силовой линии. Для бесконечно длинного проводника силовыми линиями являются окружности. Направление силовой линии (а значит, и направление вектора
направлен по касательной к силовой линии. Для бесконечно длинного проводника силовыми линиями являются окружности. Направление силовой линии (а значит, и направление вектора 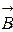 ) определяется по правилу правого винта (рис. 9).
) определяется по правилу правого винта (рис. 9).
3.4 Магнитная индукция поля, создаваемого отрезком проводника с током:
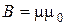
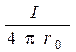 (
( 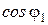 -
- 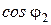 ),
),
где 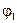 ,
, 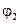 - углы между направлением тока в проводнике и радиус-векторами, проведенными от концов проводника к рассматриваемой точке А (рис. 10).
- углы между направлением тока в проводнике и радиус-векторами, проведенными от концов проводника к рассматриваемой точке А (рис. 10).
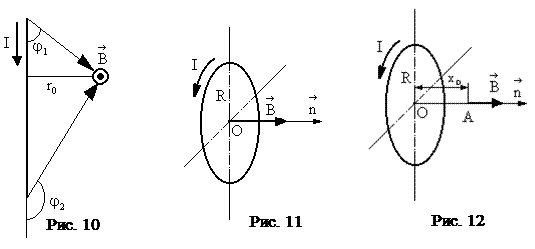 |
Вектор индукции 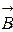 перпендикулярен плоскости чертежа, направлен к нам, и поэтому изображен точкой (рис. 10).
перпендикулярен плоскости чертежа, направлен к нам, и поэтому изображен точкой (рис. 10).
3.5 Магнитная индукция в центре кругового тока:
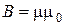
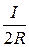 ,
,
где R – радиус кругового тока.
Вектор индукции 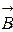 перпендикулярен плоскости кругового тока (рис. 11).
перпендикулярен плоскости кругового тока (рис. 11).
3.6 Магнитная индукция на оси кругового тока:
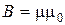
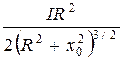 ,
,
где x 0 - расстояние от центра витка до точки, в которой определяется магнитная индукция.
Вектор индукции 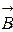 направлен вдоль оси контура (рис. 12).
направлен вдоль оси контура (рис. 12).
3.7 Магнитная индукция поля, создаваемого бесконечно длинным соленоидом в средней его части (или тороида на его оси):
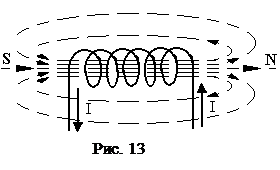
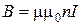 ,
,
где n – число витков, приходящихся на единицу длины соленоида; I – сила тока в соленоиде.
Линии 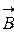 поля соленоида показаны на рис. 13.
поля соленоида показаны на рис. 13.
3.8 Принцип суперпозиции магнитных полей: магнитная индукция результирующего поля равна векторной сумме магнитных индукции 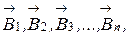 складываемых полей, т.е.
складываемых полей, т.е.
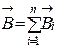 .
.
3.9 Закон Ампера. На каждый элемент тока 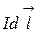 в магнитном поле индукции
в магнитном поле индукции 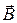 действует сила:
действует сила:
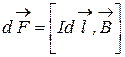 ;
; 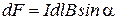 ,
,
где 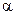 - угол между элементом тока
- угол между элементом тока 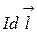 и вектором
и вектором 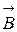 .
.
Для однородного поля ( 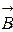 =const) и прямого отрезка проводника закон Ампера:
=const) и прямого отрезка проводника закон Ампера:
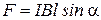 ,
,
где 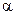 - угол между направлением тока в проводнике и вектором магнитной индукции
- угол между направлением тока в проводнике и вектором магнитной индукции 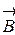 .
.
3.10 Сила взаимодействия двух прямых бесконечно длинных параллельных проводников с токами 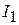 и
и 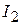 , находящихся на расстоянии
, находящихся на расстоянии 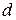 друг от друга, рассчитанная на отрезок проводника длиной l:
друг от друга, рассчитанная на отрезок проводника длиной l:
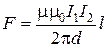 .
.
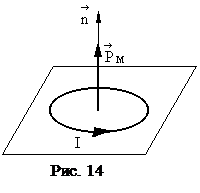 3.11 Магнитный момент плоского контура с током:
3.11 Магнитный момент плоского контура с током:
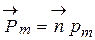 ;
; 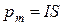
где 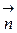 - единичный вектор положительной нор-мали к плоскости контура,
- единичный вектор положительной нор-мали к плоскости контура, 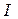 - сила тока, протекаю-щего по контуру,
- сила тока, протекаю-щего по контуру, 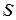 - площадь контура (рис. 14).
- площадь контура (рис. 14).
3.12 Механический (вращающий) момент, действующий на контур с током в однородном магнитном поле:
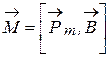 ;
; 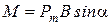 ,
,
где 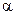 - угол между векторами
- угол между векторами 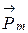 и
и 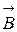 .
.
3.13 Сила 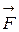 , действующая на заряд, движущийся со скоростью
, действующая на заряд, движущийся со скоростью 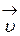 в магнитном поле с индукцией
в магнитном поле с индукцией 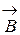 :
:
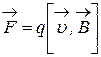 ;
; 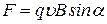 ,
,
где 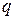 - заряд частицы;
- заряд частицы; 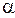 - угол между векторами
- угол между векторами 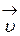 и
и 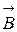 .
.
Если имеются одновременно электрическое 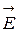 и магнитное поле
и магнитное поле 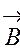 , сила, действующая на заряженную частицу (сила Лоренца):
, сила, действующая на заряженную частицу (сила Лоренца):
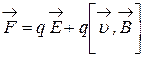 .
.
3.14 Магнитный поток Ф через плоский контур площадью 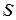 :
:
· в случае однородного поля и плоского контура
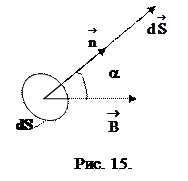
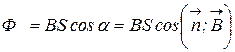 ,
,
· в случае неоднородного поля
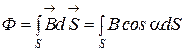 ,
,
где 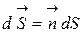 вектор, модуль которого равен dS , а направление совпадает с направлением единичного вектора нормали
вектор, модуль которого равен dS , а направление совпадает с направлением единичного вектора нормали 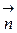 к элементу поверхности. (рис.15).
к элементу поверхности. (рис.15).
3.15 Потокосцепление, т.е. полный магнитный поток, сцепленный со всеми витками соленоида или тороида:
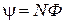 или
или 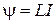 ,
,
где  - магнитный поток через один виток;
- магнитный поток через один виток; 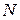 - число витков соленоида или тороида; L – индуктивность контура.
- число витков соленоида или тороида; L – индуктивность контура.
3.16 Работа по перемещению замкнутого контура в магнитном поле:
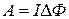 ,
,
где 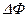 - изменение магнитного потока, пронизывающего поверхность, ограниченную контуром;
- изменение магнитного потока, пронизывающего поверхность, ограниченную контуром; 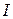 - сила тока в контуре.
- сила тока в контуре.
3.17 Закон электромагнитной индукции Фарадея:
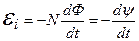 ,
,
где 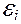 - электродвижущая сила индукции, возникающая в контуре при изменении магнитного потока. Этот закон является универсальным: ЭДС
- электродвижущая сила индукции, возникающая в контуре при изменении магнитного потока. Этот закон является универсальным: ЭДС 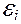 не зависит от способа изменения магнитного потока.
не зависит от способа изменения магнитного потока.
3.18 Разность потенциалов на концах провода длиною l, движущегося в магнитном поле со скоростью 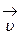 :
:
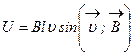 .
.
3.19 Индуктивность соленоида (тороида):
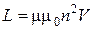 ,
,
где 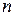 -число витков на единицу длины соленоида (тороида); V-объем соленоида.
-число витков на единицу длины соленоида (тороида); V-объем соленоида.
3.20 Электродвижущая сила самоиндукции 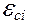 , возникающая в замкнутом контуре при изменении в нем тока:
, возникающая в замкнутом контуре при изменении в нем тока:
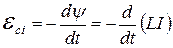 ,
,
если контур не деформируется и магнитная проницаемость среды не изменяется (L=const):
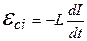 .
.
3.21 Экстратоки самоиндукции:
· при замыкании цепи
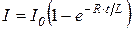 ,
,
· при размыкании цепи
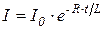 ,
,
где 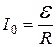 - установившийся ток (t®¥) при замыкании цепи или начальное значение тока (t=0) при размыкании цепи;
- установившийся ток (t®¥) при замыкании цепи или начальное значение тока (t=0) при размыкании цепи; 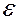 ¾ ЭДС источника тока; R – сопротивление контура.
¾ ЭДС источника тока; R – сопротивление контура.
3.22 Энергия магнитного поля, сцепленного с контуром:
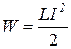 .
.
3.23 Объемная плотность энергии магнитного поля (энергия, заключенная в единице объема):
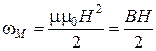 .
.
3.24 Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего контур:
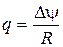 или
или 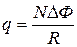
Пример 7.
Бесконечно длинный прямой провод согнут под прямым углом. По проводнику течет ток I=100 А. Вычислить магнитную индукцию 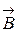 в точке, лежащей на внутренней биссектрисе угла и удаленной от вершины угла на а=100 см (среда - вакуум).
в точке, лежащей на внутренней биссектрисе угла и удаленной от вершины угла на а=100 см (среда - вакуум).
Дано: I =100 А, a=1 м, m=1.
Найти: B.
Решение.
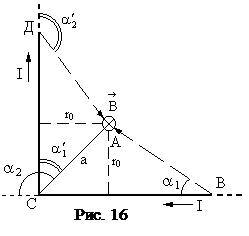 Изогнутый провод можно рассматривать как два провода, концы которых соединены в точке С. Искомая индукция
Изогнутый провод можно рассматривать как два провода, концы которых соединены в точке С. Искомая индукция 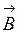 в точке А (рис. 16) является векторной суммой индукции
в точке А (рис. 16) является векторной суммой индукции 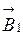 и
и 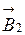 , создаваемых в этой точке токами, текущими в каждом из двух проводов ВС и СД, являющихся сторонами угла ВСД, то есть
, создаваемых в этой точке токами, текущими в каждом из двух проводов ВС и СД, являющихся сторонами угла ВСД, то есть
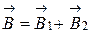 .
.
В соответствии с правилом буравчика вектора 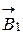 и
и 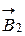 , будут направлены перпендикулярно плоскости угла и направлены от нас. Это позволяет векторное равенство заменить скалярным:
, будут направлены перпендикулярно плоскости угла и направлены от нас. Это позволяет векторное равенство заменить скалярным:
В=В1+В2.
Действительно, магнитная индукция поля, создаваемого отрезком прямолинейного проводника с током, выражается формулой:
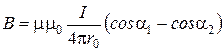 .
.
Согласно этой формуле:

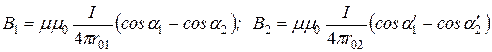 , (15)
, (15)
где r01, r02–кратчайшие расстояния от точки поля А до проводников ВС и СД соответственно (в нашем случае r01=r02=r0 согласно свойствам биссектрисы угла); a1 a2 – углы , образованные направлением тока в проводнике ВС и радиусами – векторами, проведенными от концов проводника ВС к точке поля А; 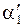
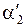 – углы , образованные направлением тока в проводнике СД и радиусами – векторами, проведенными от концов проводника СД к точке поля А (рис. 16);
– углы , образованные направлением тока в проводнике СД и радиусами – векторами, проведенными от концов проводника СД к точке поля А (рис. 16);
В нашем случае a1=00; a2=1800 (cos1800= ‑cos00= -1), 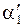 =450,
=450, 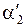 =1350.
=1350.
Соотношения между ними:
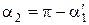 ;
; 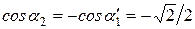 .
.
Тогда выражения ( 15 ) примут вид:
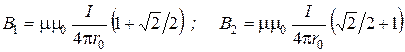 ,
,
откуда В1=В2.
Формула для вычисления результирующей индукции поля в точке А примет вид:
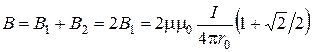 .
.
Заметив, что
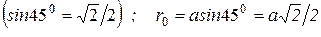 ,
,
получим:
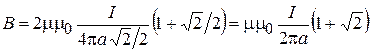 .
.
Проведем вычисления:
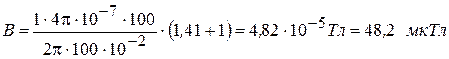 .
.
Пример 8.
Квадратная рамка со стороной а=2 см, содержащая 100 витков тонкого провода, подвешена на упругой нити, постоянная кручения С, которая равна 10 мкН×м/град. Плоскость рамки совпадает с направлением линий индукции внешнего магнитного поля. Определите индукцию внешнего магнитного поля, если при пропускании по рамке тока силой I=1 А она повернулась на угол j=600.
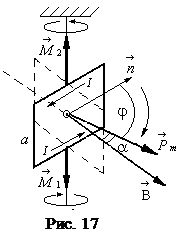
Дано: а=2 см =2×10-2 м, N=100 витков, C=10мкН×м/град =10×10-6 Н×м/град, I=1 А, j=600.
Найти: B .
Решение.
Индукция В внешнего поля может быть найдена из условия равновесия рамки в поле. Рамка будет находиться в равновесии, если сумма механических моментов, действующих на нее, будет рана нулю:
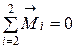 . (16)
. (16)
В данном случае на рамку действуют два момента ( рис 17 ): М1 – момент сил, с которым внешнее магнитное поле действует на рамку с током, М2 – момент упругих сил, возникающих при закручивании нити, на которой рамке подвешена. Следовательно, формула (16) может быть переписана в виде:
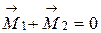 .
.
Выразив М1, М2 в этом равенстве через величины, от которых зависят моменты сил, получим:
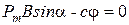 , (17)
, (17)
где a - угол между нормалью к плоскости рамки и направлением линий индукции магнитного поля; j - угол, на который поворачивается рамка.
Знак минус перед моментом М2 означает, что этот момент противоположен по направлению моменту М1.
Магнитный момент рамки:
Pm = ISN,
где I- сила тока в рамке; S – площадь рамки, S = a 2; N – число витков.
Тогда равенство (17) можно записать в виде:
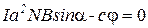 .
.
Откуда
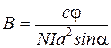 . (18)
. (18)
Из рисунка 17 видно, что 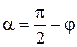 , значит, sina=cosj .С учетом этого равенство 18 примет вид:
, значит, sina=cosj .С учетом этого равенство 18 примет вид:
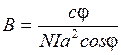 .
.
Проведем вычисления:
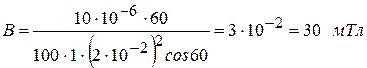 .
.
Пример 9.
Протон, имеющий скорость u = 104 м/с, влетел в однородное магнитное поле с индукцией В=0,01Тл (рис 18). Вектор скорости протона направлен под углом a=600 к линиям индукции. Определить траекторию движения протона, ее параметры, а также путь S, пройденный протоном по траектории за время t=10 мкс.
Дано: u =104 м/с, В=0,01 Тл, a=600, t=10 мкс =10×10-6 c, mp=1,67×10-27 кг; qp=1,6×10-19 Кл (характеристики протона берем из таблицы IV Приложения).
Найти S .
Решение.
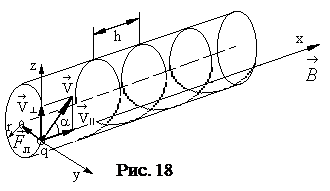 Известно, что на заряженную частицу, влетевшую в магнитное поле, действует сила Лоренца
Известно, что на заряженную частицу, влетевшую в магнитное поле, действует сила Лоренца
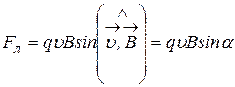 .
.
Эта сила, перпендикулярная вектору скорости, не совершает работы, поэтому кинетическая энергия протона и модуль вектора скорости остаются неизменными. Следовательно, путь, пройденный по траектории,
S = u × t .
Подставив значения u и t, получим:
S=104×10×10-6=0,1 м=10 см.
Для описания траектории протона удобно представить вектор скорости 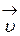 как сумму составляющих, одна из которых
как сумму составляющих, одна из которых 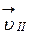 направлена по линиям ин-дукции, вторая
направлена по линиям ин-дукции, вторая 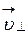 - перпендикулярна им.
- перпендикулярна им.
Составляющая скорости 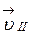 в магнитном поле не изменяется ни по модулю, ни по направлению и обеспечивает перемещение протона вдоль силовой линии. (действием силы тяжести можно пренебречь).
в магнитном поле не изменяется ни по модулю, ни по направлению и обеспечивает перемещение протона вдоль силовой линии. (действием силы тяжести можно пренебречь).
Составляющая скорости 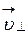 в результате действия силы Лоренца будет изменяться только по направлению. Сила Лоренца
в результате действия силы Лоренца будет изменяться только по направлению. Сила Лоренца 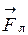 (рис 18) сообщает протону нормальное ускорение, так как
(рис 18) сообщает протону нормальное ускорение, так как 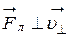 и вызывает вращение по окружности в плоскости, перпендикулярной линиям индукции. Таким образом, протон участвует в двух движениях: равномерном и прямолинейном со скоростью
и вызывает вращение по окружности в плоскости, перпендикулярной линиям индукции. Таким образом, протон участвует в двух движениях: равномерном и прямолинейном со скоростью 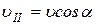 , параллельной линиям индукции (вдоль оси OX), и равномерном вращении по окружности в плоскости yOz со скоростью
, параллельной линиям индукции (вдоль оси OX), и равномерном вращении по окружности в плоскости yOz со скоростью 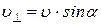 .
.
В результате одновременного участия в движениях по окружности и по прямой протон будет двигаться по винтовой линии радиусом r и шагом h .
Радиус окружности, по которой движется протон, найдем следующим образом. Сила Лоренца 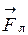 сообщает протону нормальное ускорение
сообщает протону нормальное ускорение 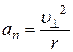 . По второму закону Ньютона:
. По второму закону Ньютона: 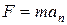 , где
, где 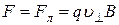 .
.
Тогда 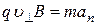 ,
,
откуда 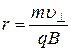 или
или 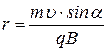 .
.
Выполним вычисления:
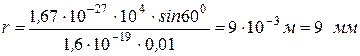 .
.
Шаг винтовой линии равен пути, пройденному протоном вдоль поля со скоростью 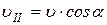 за время, равное периоду обращения T:
за время, равное периоду обращения T:
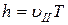 . (19)
. (19)
Период обращения связан с перпендикулярной составляющей скорости соотношением
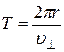 .
.
Подставив это выражение в формулу 19, найдем шаг винтовой линии:
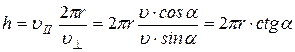 .
.
Произведя подстановку числовых значений, получим:
h=2×3,14×9×10-3×ctg600=3,3×10-2 м=3,3 см.
Пример 10
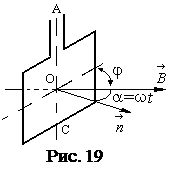
В однородном магнитном поле с индукцией B=0,1 Тл равномерно вращается рамка, содержащая N=1000 витков, с частотой n=10 с-1, площадь рамки s=150 см2 (рис 19). Определить мгновенное значение ЭДС ( 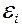 )для тех моментов времени, когда плоскость катушки составляет с линиями поля угол j=600.
)для тех моментов времени, когда плоскость катушки составляет с линиями поля угол j=600.
Дано: B=0,1 Тл, j=600, s=150см2=150×10-4 м2,
N = 1000 витков.
Найти: 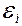 .
.
Решение.
Мгновение значение ЭДС индукции 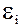 опреде-ляется основным уравнением электромагнитной индукции Фарадея – Максвелла:
опреде-ляется основным уравнением электромагнитной индукции Фарадея – Максвелла:
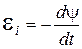 . (20)
. (20)
Потокосцепление:
y=N Ф,
где N – число витков катушки, пронизываемых магнитным потоком Ф.
Подставив выражение для потокосцепления в формулу (20), получим
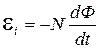 (21)
(21)
При вращении катушки (рис 19) магнитный поток Ф, пронизывающий катушку в момент времени t, изменяется по закону
Ф=B × S × cosa=B × S × coswt,
где В – магнитная индукция; S - площадь рамки; a - угол между нормалью к плоскости рамки и направлением вектора индукции поля 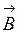 ; w - круговая частота.
; w - круговая частота.
Угловая скорость вращения постоянна, следовательно, 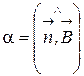 изменяется со временем по закону a=wt, если принять, что в начальный момент плоскость рамки перпендикулярна к линиям индукции. Подставив в формулу (21) выражение магнитного потока Ф и продифференцировав по времени, найдем мгновенное значение ЭДС индукции:
изменяется со временем по закону a=wt, если принять, что в начальный момент плоскость рамки перпендикулярна к линиям индукции. Подставив в формулу (21) выражение магнитного потока Ф и продифференцировав по времени, найдем мгновенное значение ЭДС индукции:
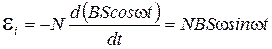 . (22)
. (22)
Круговая частота w связана с частотой вращения n соотношением w=2pn. Подставив w в формулу (22), получим:
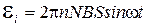 .
.
Заметив, что 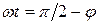 (рис19), мгновенное значение ЭДС индукции для заданных моментов времени будет равно
(рис19), мгновенное значение ЭДС индукции для заданных моментов времени будет равно
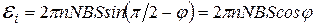 .
.
Проведем вычисления:
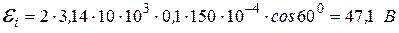 .
.
Пример 11.
В магнитном поле, индукция которого равна 0,1 Тл, помещена квадратная рамка из медной проволоки. Площадь поперечного сечения проволоки S0=1 мм2, площадь рамки S=25 см2, нормаль к плоскости рамки направлена по силовым линиям поля. Какое количество электричества q пройдет по контуру рамки при исчезновении магнитного поля?
Дано: B =0,1 Тл, S0=1 мм2 =1×10-6 м2, S=25 см2 =25×10-4 м2,rмеди=1,7×10-8Ом×м.
Найти q.
Решение.
При выключении магнитного поля произойдет изменение магнитного потока. Вследствие этого в рамке возникнет ЭДС индукции, определяемая основным законом электромагнитной индукции:
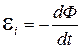 .
.
Возникшая ЭДС индукции вызовет в рамке индукционный ток, мгно-венное значение которого можно определить, воспользовавшись законом Ома для полной цепи:
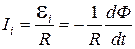 ,
,
где R- сопротивление рамки.
Так как мгновенное значение индукционного тока 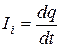 , то заряд dq, который протекает через поперечное сечение рамки за время dt, будет равен
, то заряд dq, который протекает через поперечное сечение рамки за время dt, будет равен
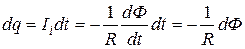 .
.
Проинтегрировав это выражение, найдем полный заряд:
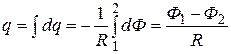 .
.
Заметим, что при выключенном поле Ф2=0, тогда
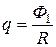 .
.
Найдем магнитный поток Ф1. По определению магнитного потока:
Ф1=BScos a ,
где S – площадь рамки, a - угол между нормалью к плоскости рамки и вектором индукции, в нашем случае a=00.
Сопротивление проволоки материала, из которого сделана рамка:
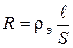 , (23)
, (23)
где rэ - удельное сопротивление материала, из которого сделана рамка; l – длина проволоки, равная периметру рамки l=4a; a – сторона рамки, 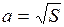 .
.
Произведя подстановки в формулу (23), получим:
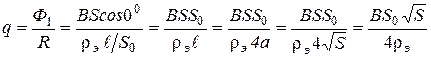 .
.
Воспользовавшись таблицей I Приложения, запишем rмеди=1,7×10-8 Ом×м.
Проведем вычисления: 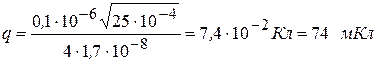 .
.
Контрольная работа № 3
Контрольная работа № 3 включает решение восьми задач. Вариант контрольной работы выбирается по последней цифре шифра, номера задач – по таблице. Необходимые справочные данные приведены в Приложении.
| Номер варианта | Номера задач | |||||||
| 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| 1 | 1 | 11 | 21 | 31 | 41 | 51 | 61 | 71 |
| 2 | 2 | 12 | 22 | 32 | 42 | 52 | 62 | 72 |
| 3 | 3 | 13 | 23 | 33 | 43 | 53 | 63 | 73 |
| 4 | 4 | 14 | 24 | 34 | 44 | 54 | 64 | 74 |
| 5 | 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 |
| 6 | 6 | 16 | 26 | 36 | 46 | 56 | 66 | 76 |
| 7 | 7 | 17 | 27 | 37 | 47 | 57 | 67 | 77 |
| 8 | 8 | 18 | 28 | 38 | 48 | 58 | 68 | 78 |
| 9 | 9 | 19 | 29 | 39 | 49 | 59 | 69 | 79 |
1. Электрическое поле создано двумя бесконечными параллельными пластинами, несущими равномерно распределенный по площади заряд с поверхностными плотностями s1=5×10-7 Кл/м2 и s2=3×10-7 Кл/м2. Определить напряженность Е поля между пластинами и вне пластин.
2. Две бесконечно длинные равномерно заряженные нити с линейными плотностями зарядов t1=6×10-9 Кл/м и t2= - 3×10-9 Кл/м расположены параллельно на расстоянии 12 см друг от друга. Установить геометрическое место точек, где результирующая напряженность электрического поля равна нулю.
3. Две длинные прямые параллельные нити находятся на расстоянии d=5 см друг от друга, на нитях равномерно распределены заряды с линейными плотностями t1= - 5 нКл/м и t1=10 нКл/м. Определить напряженность электрического поля Е в точке, удаленной от первой нити на расстояние r 1 = 3 см и от второй на расстояние r 2 = 4 см.
4. Металлическому полому шару сообщили заряд q=I нКл. Радиус шара R=15 cм. Определить напряженность Е и потенциал поля j: I) вне шара на расстоянии r=10 см от его поверхности; 2) на поверхности шара; 3) в центре шара.
5. Две бесконечные параллельные пластины равномерно заряжены с поверхностными плотностями s1=10 нКл/м2 и s2= - 30 нКл/м2. Определить силу взаимодействия между пластинами, приходящуюся на площадь S , равную I м2.
6. Два неодинаковых точечных заряда q1 и q 2 находятся на расстоянии r друг от друга. Найти положение точки, в которой напряженность Е поля равна нулю. Рассмотреть случаи: а) для одноименных зарядов; б) для разноименных зарядов. Найти потенциал поля в этих точках.
7. В вершинах правильного треугольника со стороной а = 4 см расположены два положительных и один отрицательный заряды, равные по модулю: ïq 1ï= ïq 2ï= ïq 3ï=1 нКл. Определить напря-женность и потенциал поля в центре треугольника.
8. B двух противоположных вершинах квадрата, сторона которого а=30см, находятся одинаковые заряды q=0,2 мкКл каждый. Найти напряженность и потенциал электрического поля в двух других вершинах квадрата.
9. Две бесконечные пластины, расположенные под прямым углом друг к другу несут равномерно распределенные по площади заряды с поверхностными плотностями s1=1 нКл/м2 и s2=2 нКл/м2. Опре-делить напряженность поля, создаваемого пластинами.
10. Тонкое кольцо радиусом R=10 см равномерно заряжено. Линейная плотность заряда t=20 нКл/см. Определить силу F . действующую на заряд q=10 нКл, находящийся в точке, лежащей на перпендикуляре, проходящем через центр кольца, на расстоянии а=10 см от него.
11. По тонкому кольцу радиусом R=10 см равномерно распределен заряд с линейной плотностью t=10 нКл/м. Определите потенциал j в точке, лежащей в центре кольца.
12. По тонкому кольцу радиусом R=30 см равномерно распределен заряд с линейной плотностью t=20 мкКл/м. Определите потенциал в точке, лежащей на оси кольца на расстоянии а= 5 см от центра.
13. По тонкому полукольцу радиусом R =10 см равномерно распределен заряд с линейной плотностью t=15 нКл/см. Определите потенциал j в точке, лежащей в центре кривизны.
14. На отрезке прямого провода равномерно распределен заряд с линейной плотностью t=1 мкКл/м. Определите работу сил поля по перемещению заряда q=1 нКл из точки В в точку С (рис.20)
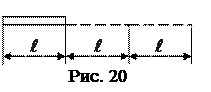
15. Два заряда q1 = 4×IO-7 Кл и q2= - 6×IO-7 Кл находятся на расстоянии 10 см друг от друга. Найти потенциал той точки поля, где напря-женность равна нулю
16. Тонкий стержень согнут в полукольцо. Стержень заряжен, линейная плотность заряда t=133 нКл/м. Какую работу надо совершить, чтобы перенести заряд q= 6,7 нКл из центра полукольца в бесконечность?
17. Поле образовано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда s = 10-9 Кл/м2. Определить раз-ность потенциалов двух точек поля, отстоящих от плоскости на расстоянии r 1=5 см и r 2= 10 см по силовой линии.
18. В керосине (e=2) на расстоянии 5 см друг от друга находятся два заряда q1=20 нКл и q2=30 нКл. Определить напряженность и потен-циал электрического поля в точке, лежащей на перпендикуляре, восстановленном к середине прямой, соединяющей заряды, на расстоянии, равном половине расстояния между зарядами.
19. Две бесконечные параллельные плоскости находятся на расстоянии d=1 см друг от друга. Плоскости несут равномерно распределенные по поверхностям заряды с плотностями s1=0,2 мкКл/м2 и s2=0,5мкКл/м2. Найти разность потенциалов Dj между плоскостями.
20. Металлический шарик диаметром d=2 см заряжен отрицательно до потенциала j=300 В. Сколько электронов находится на поверхности шарика? Определить значение и направление градиента потенциала в точке, удаленной от поверхности заряженного шара на расстояние а=2 см.
21. Пылинка массой m= 5 мг, несущая на себе N=10 электронов, прошла в вакууме ускоряющую разность потенциалов Dj=1 мВ. Какова кинетическая энергия пылинки? Какую скорость приобрела пылинка?
22. Электрон, обладающий кинетической энергией Т=5 эВ, влетел в однородное электрическое поле в направлении линий напряжен-ности. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов Dj= 2 В?
23. Пылинка массой m=20×10-6 г, несущая на себе заряд q= 40 нКл, влетела в электрическое поле в направлении линий напряженности. После прохождения разности потенциалов 100 B пылинка имела скорость 30м/с. Определить скорость пылинки до того, как она влетела в электрическое поле.
24. Протон, начальная скорость которого V 0=105 м/с, влетел в однородное электрическое поле (Е=300 В/см) так, что вектор скорости совпал с направлением линий напряженности. Какой путь должен пройти протон в направлении линий напряженности поля, чтобы его скорость удвоилась?
25. При бомбардировке неподвижного ядра калия 19К39 a-.частицей сила отталкивания между ними достигла 100 Н. На какое наименьшее расстояние приблизилась a- частица к ядру атома калия? Какую скорость имела a-частица вдали от ядра? Влиянием электронной оболочки атома калия пренебречь.
26. Пылинка массой m=4×1O-10 кг с зарядом q=10-16 Кл попадает в поле заряженного шарика, имея скорость 10 см/с, направленную к центру шарика. На какое расстояние она сможет приблизиться к шарику, заряд которого 109 Кл?
27. Электрон перемещается от одной пластины плоского конденсатора до другой. Разность потенциалов между пластинами 300 В, расстояние между ними 5 мм. Определите: а) скорость, с которой электрон достигнет другой пластины (V 0=0); б) время его движения; в) поверхностную плотность заряда на пластинах.
28. Длинный цилиндр радиусом R=I см равномерно заряжен с линейной плотностью t=10-5 Кл/м. Попавшая в поле цилиндра a-частица перемещается вдоль силовой линии от поверхности цилиндра до точки, находящейся на расстоянии 4 см от его поверхности. Как при этом изменится энергия a- частицы?
29. 

 Поверхность нагретой отрицательно заряженной нити электрон покидает со скоростью V 0=20 м/с. Какую скорость он будет иметь на расстоянии R=2 см от ее центра? Линейная плотность заряда нити t=-2×10-9 Кл/м, радиус нити r=0,5 мм.
Поверхность нагретой отрицательно заряженной нити электрон покидает со скоростью V 0=20 м/с. Какую скорость он будет иметь на расстоянии R=2 см от ее центра? Линейная плотность заряда нити t=-2×10-9 Кл/м, радиус нити r=0,5 мм.
30. 


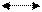

 Бесконечная прямая нить несет равномерно распределенный по длине нити заряд, линейная плотность заряда нити t=0,1 мкКл/м. Определить работу сил электрического поля при перемещении заряда q=50 нКл из точки 1 в точку 2 (рис.21).
Бесконечная прямая нить несет равномерно распределенный по длине нити заряд, линейная плотность заряда нити t=0,1 мкКл/м. Определить работу сил электрического поля при перемещении заряда q=50 нКл из точки 1 в точку 2 (рис.21).
31. Что покажет вольтметр (рис. 22), сопротивление которого 300 Ом. Исходные данные: 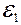 =
= 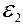 =2,2 В, R 1=100 Ом, R 2=200 Ом, R 3=300 Ом, R 4=400 Ом. Внутренним сопротивлением источников пренебречь.
=2,2 В, R 1=100 Ом, R 2=200 Ом, R 3=300 Ом, R 4=400 Ом. Внутренним сопротивлением источников пренебречь.
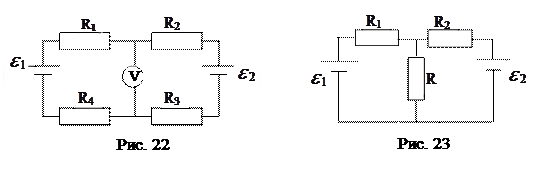
32. При каком соотношении между сопротивлениями и ЭДС источников в цепи (рис.23) ток через вторую батарею не идет?
33.  Три источника тока с электродвижущими силами
Три источника тока с электродвижущими силами 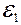 =2,5 В,
=2,5 В, 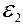 =2 В,
=2 В, 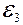 =1,5 В и сопротивлениями R 1=2 Ом, R 2=3 Ом, R 3=0,8 Ом соединены, как показано на рис. 24. Определить токи в сопротивлениях. Сопротивлением источников пренебречь.
=1,5 В и сопротивлениями R 1=2 Ом, R 2=3 Ом, R 3=0,8 Ом соединены, как показано на рис. 24. Определить токи в сопротивлениях. Сопротивлением источников пренебречь.
34. Найдите величину токов в отдельных ветвях и напряжение на сопротивлении R, если 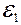 =5 В,
=5 В, 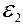 =4 В, внутренние сопротивления источников r 1=0,5 Ом, r 2=1 Ом (рис. 25).
=4 В, внутренние сопротивления источников r 1=0,5 Ом, r 2=1 Ом (рис. 25).
35.
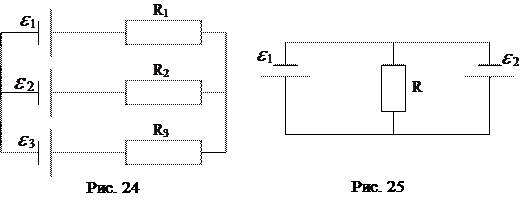 |
Найдите величины токов в отдельных ветвях цепи и напряжение на сопротивлении R, использовав условие предыдущей задачи, если в источнике 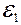 поменять полюса.
поменять полюса.
36.
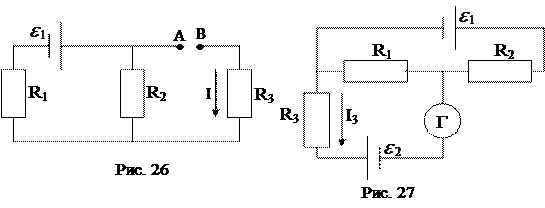 |
Три сопротивления R 1=5 Ом, R 2=1 Ом, R 3=3 Ом, а также источник тока с ЭДС 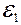 =1,4 В соединены, как показано на рис.26. Определите ЭДС источника тока, который надо подключить между точками А и В. чтобы в сопротивлении R3.шел ток силой I=1 А в направлении, указанном стрелкой. Сопротивлением источников тока пренебречь.
=1,4 В соединены, как показано на рис.26. Определите ЭДС источника тока, который надо подключить между точками А и В. чтобы в сопротивлении R3.шел ток силой I=1 А в направлении, указанном стрелкой. Сопротивлением источников тока пренебречь.
37. Электрическая цепь состоит из двух гальванических элементов, трех сопротивлений и гальванометра (рис. 27): R 1=100 Ом, R 2=50 Ом, R 3=20 Ом, 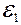 =2 В. Гальванометр регистрирует ток I 3=50 мА, идущий в направлении, указанном стрелкой. Определить ЭДС второго элемента
=2 В. Гальванометр регистрирует ток I 3=50 мА, идущий в направлении, указанном стрелкой. Определить ЭДС второго элемента 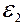 . Сопротивлением гальванометра и внутренним сопротивлением элементов пренебречь.
. Сопротивлением гальванометра и внутренним сопротивлением элементов пренебречь.
38. Определить силу тока в сопротивлении R 3 (рис.28) и напряжение на концах этого сопротивления, если 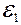 =4 В,
=4 В, 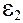 =3 В, R1=2 Ом, R2=6 Ом, R3=1 Ом. Внутренними сопротивлениями источников тока пренебречь.
=3 В, R1=2 Ом, R2=6 Ом, R3=1 Ом. Внутренними сопротивлениями источников тока пренебречь.
39.  Три источника с ЭДС
Три источника с ЭДС 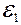 =6 В,
=6 В, 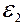 =
= 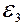 =4 В и внутренними сопротив-лениями r = 0,5 Ом каждый соединены, как показано на рис. 29, и замкнуты на сопротивлении R=4 Ом. Определить разность потенциа-лов между точками C и D (jC-jD) и между точками K и D (jK-jD).
=4 В и внутренними сопротив-лениями r = 0,5 Ом каждый соединены, как показано на рис. 29, и замкнуты на сопротивлении R=4 Ом. Определить разность потенциа-лов между точками C и D (jC-jD) и между точками K и D (jK-jD).
40. 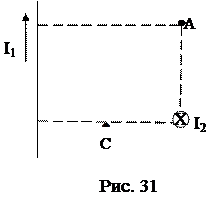

 В схеме, приведенной на рис.30,
В схеме, приведенной на рис.30, 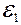 =20 В,
=20 В, 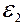 =25 В, R 1=10 Ом, R 2=15 Ом, внутренние сопротивления источников пренебрежимо малы. Определите работу, совершенную источниками, и полное количество выделившейся теплоты за интервал времени Dt = 0,5 с на R 3=82 Ом.
=25 В, R 1=10 Ом, R 2=15 Ом, внутренние сопротивления источников пренебрежимо малы. Определите работу, совершенную источниками, и полное количество выделившейся теплоты за интервал времени Dt = 0,5 с на R 3=82 Ом.
41. По двум бесконечно длинным прямым проводникам, скрещенным под прямым углом, текут токи I 1=50 А и I 2=100 А. Расстояние между проводниками d = 20 см. Определить магнитную индукцию в точке А, одинаково удаленной от обоих проводников на расстояние, равное d (рис. 31) (среда - воздух).
42. Два бесконечно длинных прямых проводника скрещены под прямым углом. По проводникам текут токи I 1=100 А, I2=50 А. Расстояние между проводниками d=20 см. Определите индукцию магнитного поля в точке С, лежащей посередине общего перпендикуляра к проводникам (рис. 31) (среда - воздух).
43. По двум длинным параллельным проводам, расстояние между кото-рыми d = 5 см, текут одинаковые токи I = 10 А. Определите индук-цию магнитного поля в точке, удаленной от каждого провода на расстояние r = 5 см , если токи текут: а) в одинаковом направлении; б) в противоположных направлениях (среда - воздух).
44. Радиусы кольцевых токов 5 и 10 А соответственно равны 12 и16 см. Они имеют общий центр и их плоскости составляют угол 45°. Найти индукцию магнитного поля в общем центре колец (среда - воздух).
45. Перпендикулярно плоскости кольцевого тока (I 1=10 А) радиусом R=20 см проходит изолированный длинный провод так, что он касается кольца. Ток в проводе равен I 2 =10 А. Найдите суммарную напряженность магнитного поля в центре кольца.
46.  Прямой бесконечный провод имеет круговую петлю радиусом R=8 см, касательную к проводу. Опреде-лить величину тока в проводе, если известно, что напряженность магнитного поля в центре петли Н=100 A/м (рис.32).
Прямой бесконечный провод имеет круговую петлю радиусом R=8 см, касательную к проводу. Опреде-лить величину тока в проводе, если известно, что напряженность магнитного поля в центре петли Н=100 A/м (рис.32).
47. По кольцевому проводнику радиусом R=5 см течет ток I 1=10 А. Параллельно плоскости кольцевого проводника на расстоянии d=2 см над его центром проходит прямой проводник с током I 2=4 А. Определите индукцию поля в центре кольца (среда - воздух).
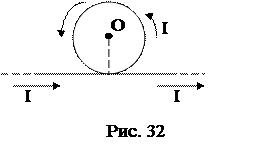
48. 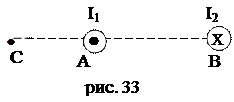 На рис.33 изображено сечение двух прямолинейных бесконечно длинных проводников с током. Расстояние АВ между проводниками равно 10 см (I 1=20 А, I 2=30 А). Найти индукцию магнитного поля, вызван-ного токами I 1 и I 2 в точке С, удаленной от первого проводника на расстояние 2 м (среда - воздух).
На рис.33 изображено сечение двух прямолинейных бесконечно длинных проводников с током. Расстояние АВ между проводниками равно 10 см (I 1=20 А, I 2=30 А). Найти индукцию магнитного поля, вызван-ного токами I 1 и I 2 в точке С, удаленной от первого проводника на расстояние 2 м (среда - воздух).
49. Два круговых витка радиусом 4 см каждый расположены в парал-лельных плоскостях на расстоянии 5 см друг or друга. По виткам текут токи I 1 = I 2=4 А. Найти индукцию магнитного поля в центре одного из витков. Задачу решить для случаев: I) токи в витках текут в одном направлении; 2) токи текут в противоположных направлениях (среда - воздух).
50.  На рис.34 изображено сечение трех прямолинейных бесконечно длин-ных проводников с током. Расстояние АВ = ВС = 5 см, I 1 = I 2 = I ; I 3 =2 I. Найти точку на прямой АС, в которой напряженность магнитного поля, вызванного токами I 1 , I 2 и I 3 , равна нулю (среда - воздух).
На рис.34 изображено сечение трех прямолинейных бесконечно длин-ных проводников с током. Расстояние АВ = ВС = 5 см, I 1 = I 2 = I ; I 3 =2 I. Найти точку на прямой АС, в которой напряженность магнитного поля, вызванного токами I 1 , I 2 и I 3 , равна нулю (среда - воздух).
51. В однородном магнитном поле с индукцией В=0,1 Тл находится прямой медный проводник сечением S 0=8 мм2, концы которого подключены гибким проводом, находящимся вне поля, к источнику постоянного тока. Определите величину тока в проводнике, если известно, что при расположении его перпендикулярно к линиям поля сила тяжести уравновешивается силой, действующей на проводник со стороны магнитного поля.
52. На двух параллельных горизонтальных шинах, расположенных на расстоянии 10 см друг от друга лежит толстый проводник массой 100 г. Шины подключены к источнику напряжения, по которому идет ток 12 А. При включении магнитного поля перпендикулярно к плоскости, в которой находятся шины, проводник приходит в равномерное движение. Определите величину индукции магнитного поля, если коэффициент трения проводника о шины 0,2.
53. Квадратная проволочная рамка расположена в одной плоскости с длинным прямым приводом так, что две ее стороны параллельны проводу. По рамке и проводу текут одинаковые токи I =1 кА, Определите силу F , действующую на рамку, если ближайшая к проводу сторона рамки находится на paccтoянии, равном ее длине.
54. По трем параллельным прямым проводам, находящимся на одинаковом расстоянии d= 10 см друг от друга, текут одинаковые токи силой I=100 А. В двух проводах направления сил токов совпадают. Вычислить силу, действующею на отрезок каждого провода длиной в 1 м.
55. Рамка гальванометра длиной 4 см, шириной 1,5 см, содержащая 200 витков тонкой проволоки, находится в магнитном поле с индукцией В=0,1 Тл. Плоскость рамки параллельна линиям индукции. Найдите механический момент, действующий на рамку, когда по ней идет ток I=1 мА.
56. Квадратная плоская катушка со стороной 4 см, состоящая из 30 витков, выполнена из медной проволоки диаметром 0,4 мм. К выводам катушки приложено напряжение U=1 В. Какой вращающий момент действует на катушку, если плоскость катушки составляет угол 30° с направлением однородного поля напряженностью Н= 100 А/м?
57. Напряженность магнитного поля Н=50 А/м. В этом поле находится плоская рамка площадью 10 см2, которая может свободно вращаться. Плоскость рамки вначале совпадала с направлением поля. Затем по рамке кратковременно пропустили ток I=1 А и рамка получила угловое ускорение 100 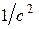 . Считая вращающий момент постоян-ным, найти момент инерции рамки.
. Считая вращающий момент постоян-ным, найти момент инерции рамки.
58. Плоская круглая рамка диаметром 10 см находится в однородном магнитном поле с напряженностью Н=10 А/м. По рамке протекает ток I=20 А. На сколько изменится вращающий момент, действующий на рамку, при повороте плоскости рамки на угол 60° к направлению поля? До поворота плоскость рамки совпадала с направлением поля. Какая при этом совершена работа?
59. Виток диаметром 20 см может вращаться около вертикальной оси, совпадающей с одним из диаметров витка. Виток установили в плоскости магнитного меридиана и пустили по нему ток I=10 A. Найдите механический момент, который нужно приложить к витку, чтобы удержать его в начальном положении. Горизонтальную составляющую индукции магнитного поля 3емли ВГ принять равной 20 мкТл.
60. В центре соленоида, имеющего 5 витков на каждый сантиметр, рас-положена плоская катушка, состоящая из 20 витков площадью 0,3 см2 каждый. Плоскость витков катушки составляет с осью соленоида угол 35°. По обмотке соленоида течет ток I 1=4 А, по обмотке катушки I 2=0.1 А. Определить вращающий момент, дейст-вующий на плоскую катушку в начальном положении; работу, совершаемую силами поля, при повороте катушки до положения устойчивого равновесия.
61. Электрон движется в магнитном поле с индукцией В=2×10-3 Тл по винтовой линии радиусом R=2 см и шагом h=5 см. С какой скоростью влетел электрон в магнитное поле?
62. Электрон влетает в однородное магнитное поле напряженностью 1500 А/м со скоростью 720 км/с, Направление скорости составляет угол 30° с направлением поля. Определить радиус и шаг винтовой линии, по которой будет двигаться электрон в магнитном поле.
63. В однородном магнитном поле (В=2 Тл) движется протон, траектория его движения представляет собой винтовую линию с радиусом 10 см и шагом 60 см. Определить кинетическую энергию протона.
64. Электрон прошел ускоряющую разность потенциалов U=800 В и, влетев в однородное магнитное поле (B=47 мкТл),стал двигаться по винтовой линии с шагом h=6 см. Определить радиус R винтовой линии.
65. Альфа-частица прошла ускоряющую разность потенциалов U=300 В и, попав в однородное магнитное поле, стала двигаться по винтовой линии радиусом R=1 см и шагом h =4 см. Определить магнитную индукцию В поля.
66. Альфа-частица прошла ускоряющую разность потенциалов U=300 В, влетев в однородное магнитное поле с индукцией В=0,1 Тл, и стала двигаться по винтовой линии радиусом R=1 см и шагом h=6,5 см. Определить отношение заряда частицы к ее массе.
67. Альфа-частица, пройдя ускоряющую разность потенциалов, стала двигаться в однородном магнитном поле о индукцией В= 50 мТл по винтовой линии с шагом h=5 см и радиусом 1 см. Определить ускоряющую разность потенциалов, которую прошла a-частица.
68. Заряд движется в вакууме прямолинейно со скоростью 10 м/с во взаимно перпендикулярных магнитном и электрическом полях. Каково должно быть отношение напряженностей этих полей, чтобы имело место такое движение? Как направлена скорость заряда относительно магнитного и электрического полей? Задачу пояснить чертежом.
69. Протон прошел ускоряющую разность потенциалов U=300 В и влетел в однородное магнитное поле (В=20 мТл) под углом 45° к линиям магнитной индукции. Определить шаг h и радиус R винтовой линии, по которой будет двигаться протон в магнитном поле.
70. Электрон влетел в однородное магнитное поле с индукцией В=30 мТл под углом a=30° к направлению линий индукции и стал двигаться по винтовой линии радиусом 190 мкм. Найти шаг винтовой линии и скорость, с которой электрон влетел в магнитное поле
71. Рамка площадью S=200 см2 равномерно вращается с частотой n=10об/с относительно оси, лежащей в плоскости рамки и перпендикулярной линиям индукции магнитного поля (В=0.2 Тл). В рамке возникает ЭДС индукции. Определить среднее значение ЭДС индукции за время, в течение которого магнитный поток, пронизывающий рамку, изменится от нуля до максимального значения?
72. Рамка, содержащая N=200 витков площадью S = ЗОО cм2 равномерно вращается в однородном магнитном поле с индукцией B=1,5×10-2 Тл. Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Определить период вращения, если максимальная ЭДС индукции, возникающая в рамке, равна 14,4 В.
73. Плоский проводящий контур, имеющий вид квадрата со стороной а=20см, находится в однородном магнитном поле, перпендикуляр-ном к его плоскости. Найти амплитудное значение индукционного тока, возникшего в контуре, если магнитное поле, пронизывающее контур, будет меняться по закону B = B 0 sinwt, где B 0=10 мТл, w=100 рад/с. Сопротивление единицы длины контура rэ=50 мОм/м. Индуктивностью контура пренебречь.
74. В однородном магнитном поле с индукцией В=0,1 Тл равномерно вращается квадратная рамка со стороной а=20 см, состоящая из N =100 витков медного провода сечением S 0=1 мм2 . Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Определите частоту вращения рамки, если максимальное значение индукционного тока, возникшего в рамке, равно 2 А.
75. На длинный прямой соленоид, имеющий диаметр сечения d =5 см и содержащий n=20 витков на один сантиметр длины, плотно надет круговой виток из медного провода сечением S 0=1,0 мм2. Найти индукционный ток в витке, если ток в обмотке соленоида увеличивают с постоянной скоростью К=100 А/с по закону I = Kt. Индуктивностью витка пренебречь.
76. Обмотка соленоида с немагнитным сердечником содержит 1100 вит-ков. Длина сердечника 60 см, площадь его поперечного сечения 100 см2. На соленоид надето изолированное кольцо того же диамет-ра. Какая ЭДС индукции возникает в кольце, если ток в соленоиде будет равномерно возрастать на 0,3 А за каждую секунду?
77. В магнитное поле помещена квадратная рамка из алюминиевого про-вода с поперечным сечением S 0=1 мм2. Плоскость рамки перпендику-лярна линиям индукции магнитного поля. Сторона рамки а=10 см. Какое количество теплоты выделится в рамке за время Dt=2 с, если магнитное поле, пронизывающее рамку, будет возрастать пропор-ционально времени В= Kt , где К=10 Тл/c?
78. В электрической цепи, содержащей резистор сопротивлением R=20 Ом и катушку индуктивностью L=0,06 Гн, течет ток I =20 А. Определить силу тока I в цепи через Dt=0,2 мкс после ее размыкания.
79.  Виток, по которому течет ток I=20 А, свободно установился в однородном магнитном поле с индукцией B=0,02 Тл. Диаметр витка d равен 10 см. Определить работу А, которую нужно совершить, чтобы повернуть виток относительно оси, совпадающей с диаметром витка, на углы a1=p/2, a2=2p.
Виток, по которому течет ток I=20 А, свободно установился в однородном магнитном поле с индукцией B=0,02 Тл. Диаметр витка d равен 10 см. Определить работу А, которую нужно совершить, чтобы повернуть виток относительно оси, совпадающей с диаметром витка, на углы a1=p/2, a2=2p.
80. 
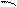 Дроссель с индуктивностью L=8 Гн и омическим сопротивлением R 1=40 Ом и лампа с сопротивление R 2=200 Ом соединены параллельно и подключены к источнику с ЭДС
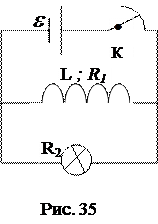
Дроссель с индуктивностью L=8 Гн и омическим сопротивлением R 1=40 Ом и лампа с сопротивление R 2=200 Ом соединены параллельно и подключены к источнику с ЭДС 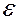 =120 B через ключ (рис.35). Определить разность потенциалов на зажимах дросселя при t1=0,01 с и t2=0,5 с после размыкания цепи.
=120 B через ключ (рис.35). Определить разность потенциалов на зажимах дросселя при t1=0,01 с и t2=0,5 с после размыкания цепи.
Приложение.
Таблица I
Удельное сопротивление материалов rэ при 00 С.
| Металл | Удельное сопротивление, нОм×м | Металл | Удельное сопротивление, нОм×м |
| Медь Алюминий | 1,70 2,53 | Железо Нихром | 9,80 110,00 |
Таблица II
Плотность вещества r.
| Вещество | Плотность, кг/м3 | Вещество | Плотность, кг/м3 |
| Медь Алюминий | 8,9×103 2,7×103 | Железо Ртуть | 7,8×103 13,6×103 |
Таблица III
Диэлектрическая проницаемость (относительная) вещества e.
| Вещество | Проницаемость | Вещество | Проницаемость |
| Парафин Стекло Вода | 2,0 6,0 81,0 | Керосин Масло (трансфор) | 2,0 2,2 |
Таблица IV
Характеристики некоторых частиц, атомов.
| Частица | Масса, кг | Заряд, Кл |
| Электрон -1e0 Протон 1p1 2a4-частица (ядро атома Гелия 2He 4) Дейтон (ядро тяжелого водорода) 1H2 | 9,11×10-31 1,67×10-27 6,64×10-27 3,35×10-27 | -1,6×10-19 +1,6×10-19 +3,2×10-19 +1,6×10-19 |
Список литературы
1. А.А Детлаф., Б.М Яворский., Курс физики (учебное пособие для вузов).- М.: Высшая школа, 2000.
2. Р.Г Геворкян. Курс физики (учеб. пособие для вузов). - М.: Высш. шк.,1979.
3. Г.А Зисман., О.М. Годес. Курс общей физики.(учеб. пособие в 3-х т.). – М.: Наука, 1974.
4. И.В. Савельев. Курс общей физики (учеб. пособие для вузов в 5-ти книгах, 4-ое издание, переработанное) – М.:Наука, 1998.
5. Т.И. Трофимова. Курс физики (учеб. пособие для студентов вузов). - М.: Высш. шк.,2002.
6. В.С. Волькенштейн Сборник задач по общему курсу физики (учеб. пособие). – М.: Наука, 1985.
7. А.Г. Чертов, А.А. Воробьев. Задачник по физике (учеб. пособие для вузов). - М.: Физматлит, 2002.
Оглавление
Рекомендации к выполнению контрольной работы ……………………….3
Основные уравнения электродинамики …………………………………….4
1. Электростатика …………………...………………………………….…4
2. Электрический ток ……………………………………...……………...16
3. Магнитное поле тока …………………………..………………………20
Контрольная работа №3………………..…………………………………….33
Приложение …………………………………………………………………..44
Список литературы ..…………………………………………………………45








