4. Расчёт параметров оптимальной динамической настройки САР с дифференциатором по методике ВТИ (Александровой Н. Д.)
2. Методика оптимизации типовой САР с дифференциатором (САР с дифференцированием промежуточного сигнала)
Исходные данные:
1) Динамика опережающего участка задана в виде инерционного звена второго порядка:
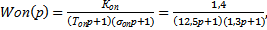 (1.1)
(1.1)
где 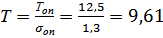 , (1.2)
, (1.2)
2) 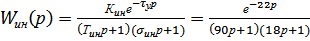 , (1.3)
, (1.3)
3)  Структурная схема САР с дифференциатором в виде направленного графа
Структурная схема САР с дифференциатором в виде направленного графа
f2
 f1 Wв(р)
f1 Wв(р)







 Хзд Wр(р) Wоп(р) Wин(р) y(t)
Хзд Wр(р) Wоп(р) Wин(р) y(t)
Хp
 -Wд(р)
-Wд(р)
 -1
-1
Рис. 1
4) 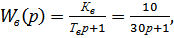 (1.4)
(1.4)
5) 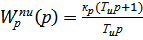 , (1.5)
, (1.5)
6) 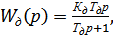 (1.6)
(1.6)
7) 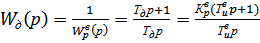 , (1.7)
, (1.7)
8) 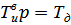 ;
; 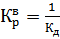 ; (1.8)
; (1.8)
9) Дифференциатор настраиваем на оптимальную отработку крайнего внешнего возмущения f2 по МПК в ЧВ. Основной регулятор настраиваем на оптимальную отработку внутреннего возмущения f1 по МЧК.
10) Т. к. для оптимизации двухконтурной САР необходимо разложить её на 2 одноконтурные, то будем считать, что динамика внутреннего контура не влияет на динамику внешнего.
Алгоритм оптимизации:
1) Декомпозиция двухконтурной САР на 2 одноконтурные. Оптимизацию начинаем с дифференциатора. Внутренний контур представим передаточной функцией 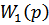 :
:
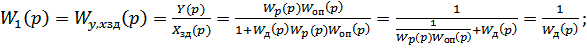 (1.9)
(1.9)
2) 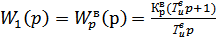 ; (1.10)
; (1.10)
3) Виртуальный ПИ-регулятор настраиваем по МПК в ЧВ на оптимальную отработку f2 по передаточной функции инерционного участка:
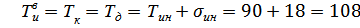 , (1.11)
, (1.11)
Для 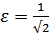 ,
, 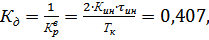 (1.12)
(1.12)
Для 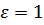 ,
, 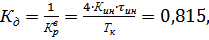 (1.13)
(1.13)
Применимо к дифференциатору, та настройка будет лучше при отработке f2, при которой произведение 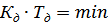 . Т. о. передаточная функция дифференциатора
. Т. о. передаточная функция дифференциатора 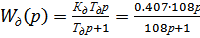 ;
;
4) Оптимизация настройки основного регулятора производится на основе внутреннего контура.
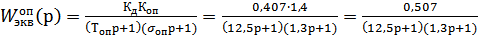 ; (1.14)
; (1.14)
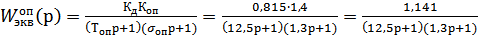 ; (1.15)
; (1.15)
5) Регулятор настраиваем по МЧК для оптимальной отработки f1.
· Для коэффициентов Вышнеградского 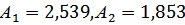 (1.16)
(1.16)

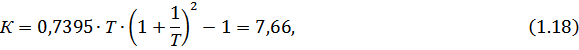
· Для коэффициентов Вышнеградского, взятых по правилу «Золотого сечения» 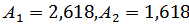 (1.19)
(1.19)

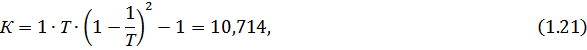
· Для коэффициентов Вышнеградского, взятых по правилу «Золотого сечения» 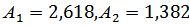 (1.22)
(1.22)

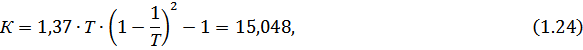
· Для коэффициентов Вышнеградского, взятых по правилу «Золотого сечения» 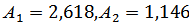 (1.25)
(1.25)

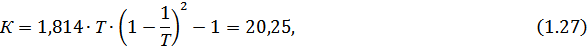
6) Находим абсолютные значения Кр
· 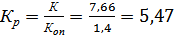 , (1.28)
, (1.28)
· 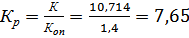 , (1.29)
, (1.29)
· 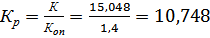 , (1.30)
, (1.30)
· 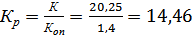 , (1.31)
, (1.31)
7) Находим относительное время регулирования
· 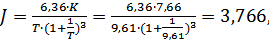 (1.32)
(1.32)
· 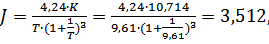 (1.33)
(1.33)
· 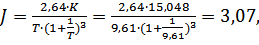 (1.34)
(1.34)
· 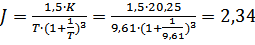 (1.35)
(1.35)
8) Находим абсолютное значение времени Ти1
· 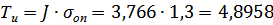 , (1.36)
, (1.36)
· 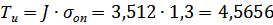 , (1.37)
, (1.37)
· 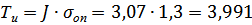 , (1.38)
, (1.38)
· 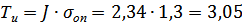 , (1.39)
, (1.39)
3. Определение оптимальных переходных процессов типовой САР с дифференциатором по методике БНТУ
Собираем структурные схемы и определяем оптимальную.
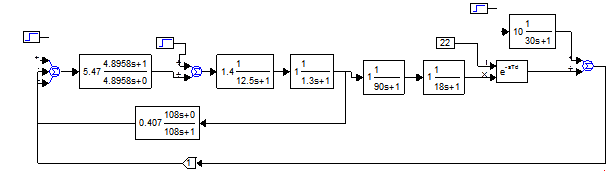
Рис. 3.1 (2,539-1,853)
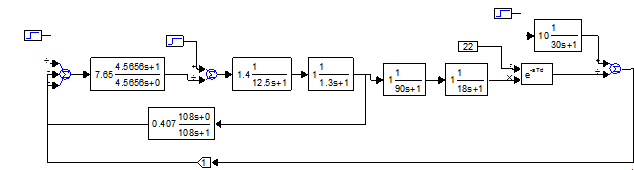
Рис. 3.2 (2,618-1,618)
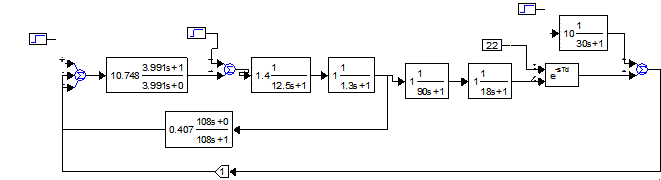
Рис.3.3 (2,618-1,382)
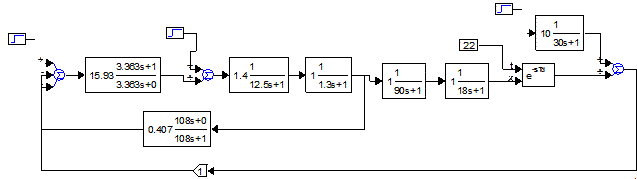
Рис. 3.4 (2,618-1,146)
График отработки внутреннего возмущения:
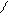



|
|
|
|
Рис. 3.5
Из полученных графиков можно сделать вывод о том, что лучше всего отрабатывает внутреннее возмущение передаточная функция с коэффициентами Вышнеградского 2,618-1,146. Об этом свидетельствуют наименьшие значения ППК: tр=385,06 с, 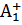 =0,0045.
=0,0045.
4. Расчёт параметров оптимальной динамической настройки САР с дифференциатором по методике ВТИ (Александровой Н. Д.)
Исходные данные:
Динамика опережающего и инерционного участков объекта регулирования заданы в виде инерционного звена первого порядка с запаздыванием (аппроксимация Кумпфмюллера)
Алгоритм расчёта:
1) По передаточной функции опережающего участка, представленной по методике БНТУ в виде инерционного звена второго порядка переводим в передаточную функцию первого порядка с запаздыванием.
Расчёт настройки САР с дифференциатором по ВТИ начинаем с расчёта настройки основного регулятора, используя передаточную функцию опережающего участка.
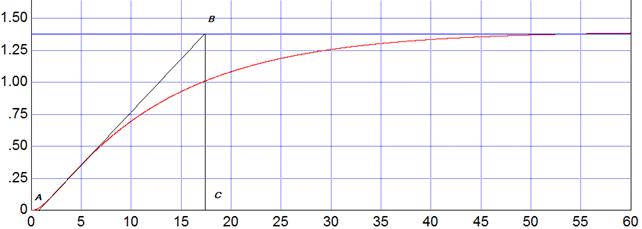
Рис. 4.1
По экспериментальному графику переходных процессов рис. 4.1 принимаем 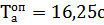 ;
; 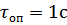 .
.
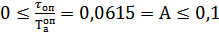 (4.1)
(4.1)
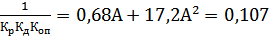 (4.2)
(4.2)
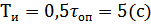 (4.3)
(4.3)
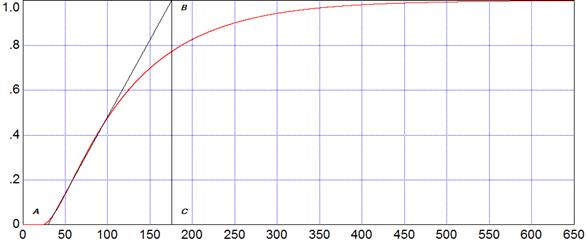
Рис. 4.2
По экспериментальному графику переходных процессов рис. 4.2 принимаем 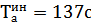 ;
; 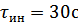 .
.
2) Для расчёта настройки дифференциатора применяем компромиссные настройки (средние между f1 и f2)
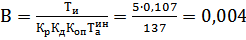 ;
; 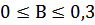 ; (4.4)
; (4.4)
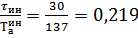 ;
; 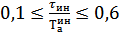 ; (4.5)
; (4.5)
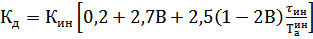 =0,754; (4.6)
=0,754; (4.6)
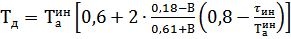 =127,83(с) (4.7)
=127,83(с) (4.7)
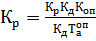 =0,762 (4.8)
=0,762 (4.8)
5. Определение оптимальных переходных процессов САР с дифференциатором по методике ВТИ
Структурная схема САР с дифференциатором, настроенная по методу ВТИ имеет вид:

Рис.5.1
График отработки задающего воздействия:
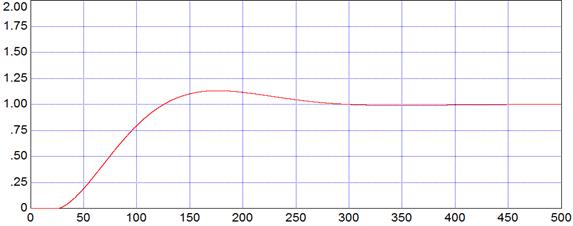
Рис. 5.2
График отработки внутреннего возмущения:
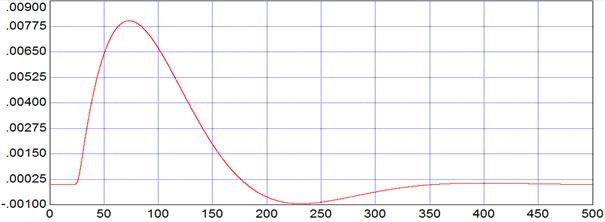
Рис. 5.3
График отработки крайнего внешнего возмущения:
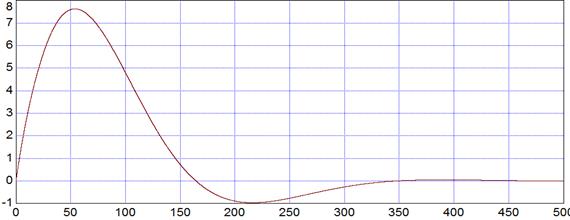
Рис. 5.4
График отработки регулирующего воздействия:
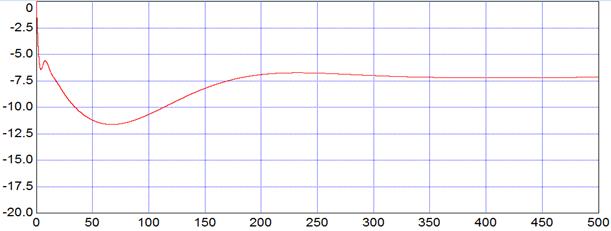
Рис. 5.5
6. Сравнение переходных процессов по методикам БНТУ и ВТИ

|

|
Графики отработки задающего воздействия: 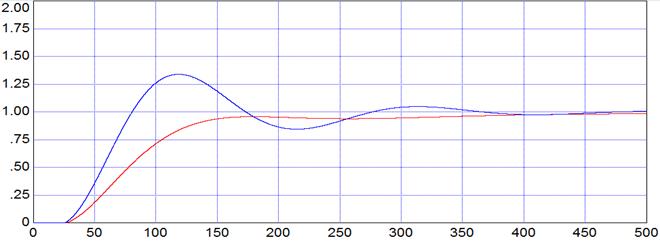
Рис.6.1


|
|
Графики отработки внутреннего возмущения: 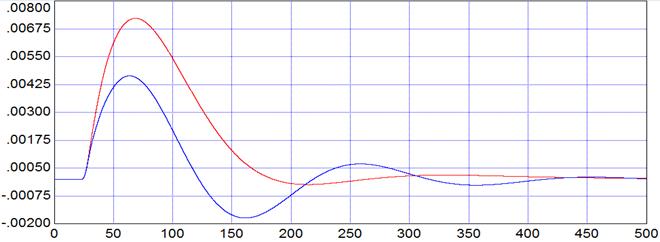
Рис. 6.2


|
|
Графики отработки крайнего внешнего возмущения: 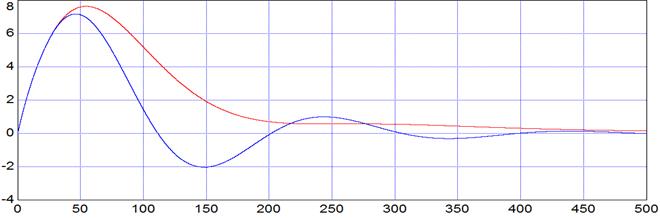
Рис. 6.3

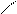
|
|
Графики отработки регулирующего воздействия: 
Рис. 6.4
7. Моделирование типовой САР с дифференциатором с целью улучшения качества переходных процессов по отношению к ВТИ с учётом максимальной величины регулирующего воздействия
Для улучшения качества переходных процессов по БНТУ подберём коэффициенты Вышнеградского по правилу «Золотого сечения»:
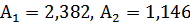 ;
;
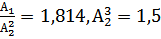 ; (7.1)
; (7.1)
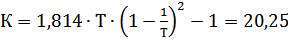 ; (7.2)
; (7.2)
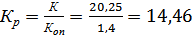 ; (7.3)
; (7.3)
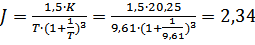 ; (7.4)
; (7.4)
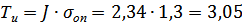 ; (7.5)
; (7.5)
Структурные схемы имеют вид: 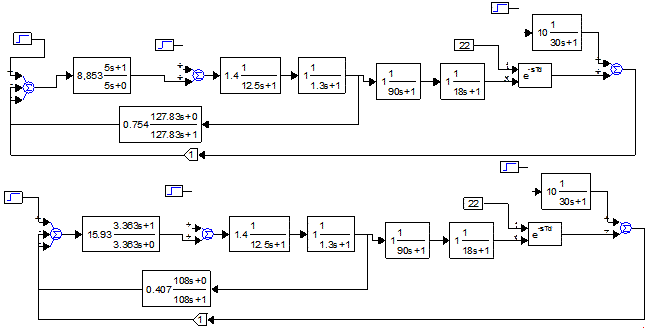
Рис. 7.1

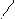
|
|
Графики отработки задающего воздействия: 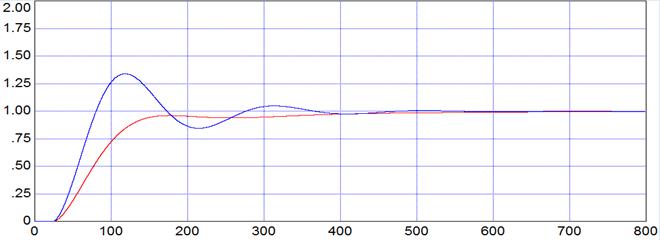
Рис. 7.2
Графики отработки внутреннего возмущения:

|

|
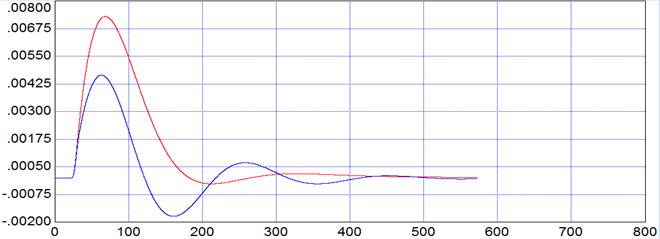
Рис. 7.3
Графики отработки крайнего внешнего возмущения:

|

|
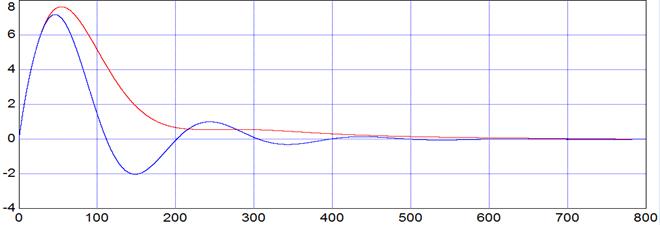
Рис. 7.4


|
|
Графики отработки регулирующего воздействия: 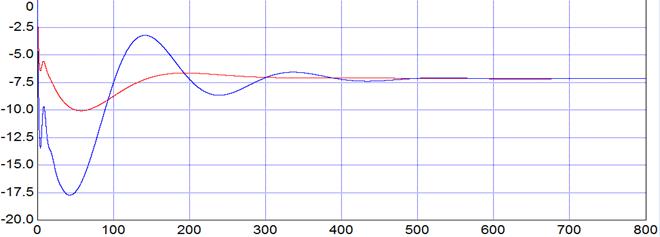
Рис. 7.5
Для анализа графиков составим таблицу ППК
| Метод
При отработке | БНТУ | ВТИ | |
| задающего воздействия хзд | tp | 470 | 536 |
| σм | 34% | -5% | |
| ψ | 0,21 | 1 | |
| А1+ | 1,34 | 0,95 | |
| А2+ | 1,048 | 1,0 | |
| внутреннего возмущения f1 | tp | 493 | 592 |
| ψ | 0,825 | 0,97 | |
| А1+ | 0,004 | 0,007 | |
| А2+ | 0,0007 | 0,0002 | |
| внешнего возмущения f2 | tp | 491 | 650 |
| ψ | 0,85 | 0,92 | |
| А1+ | 7,1 | 7,6 | |
| А2+ | 1 | 0,54 | |
| регулирующего воздействия хрег | А1- | -17,6 | -10,1 |
8. Выводы по результатам предыдущих воздействий
Типовая САР с дифференциатором, рассчитанная по методу БНТУ для коэффициентов Вышнеградского, взятых по правилу «Золотого сечения»:
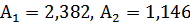 лучше отрабатывает все воздействия в сравнении с САР с дифференциатором, рассчитанной по методике ВТИ. Это следует из анализа прямых показателей качества.
лучше отрабатывает все воздействия в сравнении с САР с дифференциатором, рассчитанной по методике ВТИ. Это следует из анализа прямых показателей качества.








