! О п р е д е л е н и е: Пересечением двух множеств называют множество, состоящее из всех общих элементов этих множеств.
3. О б ъ е д и н е н и е м н о ж е с т в.
Возьмём те же два множества: А = {1, 2, 3, 4, 5, 6} и В = {5, 6, 7, 8, 9}. Составим теперь множество D таким образом, чтобы в него вошли все элементы, которые принадлежат хотя бы одному из множеств А и В.
Здесь следует ознакомить учащихся с приёмом задания объединения множеств: сперва мы выписываем все элементы множества А, а затем те элементы множества В, которые не принадлежат множеству А. Получим: D = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Множество D является объединением множеств А и В, обозначается так:
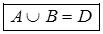
! О п р е д е л е н и е: Объединением двух множеств называют множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств.
4. У п р а ж н е н и я:
а) Верна ли запись:
1) {8, 12, 16, 20} = {12, 20, 16, 18};
2) {m, n, p, q} = {p, m, q, n};
3) {3, 4, 3, 5} = {3, 4, 5}?
б) Запишите множества, равные:
1) {2, 3, 2, 4, 2, 5}; 2) {f, f, f, m, m, m}.
в) Даны множества А = {3, 4, 5}, В = {5, 6, 7, 8}, С = {2, 4, 8} и K = {1, 3, 5, 7}. Найдите:
1) А 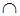 K; 5) А
K; 5) А 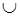 K;
K;
2) А 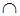 С; 6) А
С; 6) А 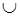 С;
С;
3) А 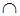 В; 7) А
В; 7) А 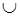 В;
В;
4) А 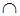 K
K 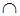 В; 8) А
В; 8) А 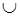 K
K 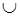 В.
В.
I I . Формирование умений и навыков.
На этом уроке отрабатываются умения задавать множества, правильно оформляя запись, а также находить пересечение и объединение множеств, пользуясь введенными определениями.
Запиши задание в тетрадь
1. № 799.
Р е ш е н и е
х = {2, 3, 5, 7, 11, 13, 17, 19};
у = {10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}.
х 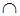 у = {11, 13, 17, 19};
у = {11, 13, 17, 19};
х 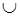 у = {2, 3, 5, 7, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}.
у = {2, 3, 5, 7, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}.
2. Найдите пересечение и объединение множеств букв, которые используются при записи слов «типография» и «фотография».
Р е ш е н и е
А = {т, и, п, о, г, р, а, ф, я} – множество букв, используемых в записи слова «типография»;
В = {ф, о, т, г, р, а, и, я} – множество букв, используемых в записи слова «фотография».
А 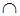 В = {т, и, о, г, р, а, ф, я},
В = {т, и, о, г, р, а, ф, я},
А 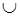 В = {т, и, п, о, г, р, а, ф, я}.
В = {т, и, п, о, г, р, а, ф, я}.
П р и м е ч а н и е. Обращаем внимание учащихся, что в этом случае А 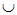 В = А.
В = А.
3. № 801 (а).
Р е ш е н и е
х = {1, 2, 3, 4}; у = {1, 2, 3, 6}.
х 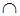 у = {1, 2, 3}; х
у = {1, 2, 3}; х 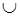 у = {1, 2, 3, 4, 6}.
у = {1, 2, 3, 4, 6}.
П р и м е ч а н и е. Подчёркиваем необходимость «упорядоченной» записи множеств, так как в этом случае будет удобнее отыскивать общие элементы множеств.
4. № 802 (а).
Р е ш е н и е
а) Чтобы число принадлежало пересечению множеств А и В, оно должно являться одновременно квадратом натурального числа и кубом натурального числа.
1= 12; 1 = 13, значит, 1 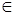 А
А 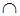 В;
В;
4 = 22, но не является кубом натурального числа, значит, 4 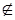 А
А 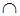 В.
В.
64 = 82, 64 = 43, значит, 64 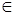 А
А 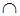 В.
В.
V. Итоги урока.
Контроль: Письменно ответьте на В о п р о сы:
1)Какие способы задания множеств существуют?
2) Какие два множества являются равными?
3) Как называется множество, в котором нет ни одного элемента?
4) Что называется пересечением двух множеств?
5) Что называется объединением двух множеств?
Домашнее задание.
1. № 800, № 801 (б), № 802 (б).
2. Укажите наибольший и наименьший элементы пересечения множества двузначных чисел, кратных 9, и множества нечётных двузначных чисел.
Четкую фотографию выполненных заданий прислать до 27 марта на адрес:
https://vk.com/id587584299








