Основные понятия теории множеств. Пересечение и объединение множеств
Четкую фотографию выполненных заданий прислать до 27 марта на адрес:
https://vk.com/id587584299
Цели: ознакомиться с основными понятиями теории множеств, операциями над множествами (пересечение и объединение множеств); сформировать умения задавать множества и проводить над ними основные операции.
Ход урока (самоподготовка)
I. Объяснение нового материала..
Читаем конспект, делаем для себя пометки.
I б л о к.
1. О с н о в н ы е п о н я т и я.
Одно из основных понятий современной математики – множество. Это понятие обычно принимается за первичное и поэтому не определяется через другие.
Когда в математике говорят о множестве (чисел, точек, функций и т. д.), то объединяют эти объекты в одно целое – множество, состоящее из этих объектов (чисел, точек, функций и т. д.). Основатель теории множеств, немецкий математик Георг Кантор (1845–1918), выразил эту мысль следующим образом: «Множество есть многое, мыслимое как единое, целое».
! Множество – это совокупность объектов, объединённых между собой по какому-либо признаку.
Слово «множество» в обычном смысле всегда связывается с большим числом предметов. Например, мы говорим, что в лесу множество деревьев, но если перед домом два дерева, в обычной речи не говорят, что перед домом «множество деревьев».
Математическое же понятие множества не связывается обязательно с большим числом предметов. В математике удобно рассматривать и «множества», содержащие 3; 2 или 1 предмет и даже «множество», не содержащее ни одного предмета (пустое множество). Например, мы говорим о множестве решений уравнения до того, как узнаем, сколько оно имеет решений.
Произвольные множества обозначают большими латинскими буквами А, В, С, ... Пустое множество, то есть множество, которое не имеет элементов, обозначается символом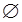 
.
О предметах, составляющих множество, говорят, что они принадлежат этому множеству, или являются его элементами. Элементы множества обозначают малыми латинскими буквами а, b, с, ... или одной какой-нибудь буквой с индексом, например а1, а2, ... , ап.
Предложение «предмет а принадлежит множеству А», или «предмет а – элемент множества А», обозначают символом а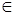 
А.
2. С п о с о б ы з а д а н и я м н о ж е с т в:
1) Множество может быть задано непосредственным перечислением всех его элементов (в произвольном порядке). В таком случае названия всех элементов множества записываются в строчку, отделяются между собой запятыми и заключаются в фигурные скобки.
Н а п р и м е р: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} – множество цифр десятичной системы счисления.
Необходимо различать объекты, обозначаемые символами а и {а}. Символом а означается предмет, символом {а} – множество, состоящее из одного элемента а (единичное множество). Перечислением всех элементов можно задать лишь конечное множество. Такие множества, как, например, множество всех натуральных (N) или всех целых чисел (Z), нельзя задать таким способом, так как мы не можем перечислить все N и все Z – таких чисел бесконечное множество.
2) Имеется другой (универсальный) способ задания множества в том смысле, что этим способом может быть задано не только конечное, но и бесконечное множество. Множество может быть задано указанием характеристического свойства, то есть такого свойства, которым обладают все элементы этого множества и не обладает ни один предмет, не являющийся его элементом.
Н а п р и м е р: {x | x – делятся на 10};
A = {a | a – число, которое меньше, чем 100}.
3. У п р а ж н е н и я:
а) Назовите известные вам множества людей (например, команда).
б) Запишите множества, элементами которых являются:
1) планеты Солнечной системы;
2) столицы государств;
3) все двузначные числа;
4) числа, делящиеся на 7.
в) Пусть А – множество чисел, на которые делится 100 без остатка. Верна ли запись:
1) 5 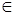А; 2) 12 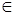А; 3) 7 
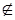А; 4) 4 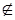А?
г) Пусть даны множества А = {а а – число, кратное двум} и В =
= {b b – число, кратное шести}.
В ы п и ш и т е:
1) два элемента, принадлежащих множеству А, но не принадлежащих множеству В;
2) два элемента, принадлежащих и множеству А, и множеству В;
3) два элемента не принадлежащих ни множеству А, ни множеству В.
II б л о к.
1. Р а в е н с т в о м н о ж е с т в.
Очень важной особенностью множества является то, что в нём нет одинаковых элементов, вернее, что все они отличны друг от друга. Это значит, можно записать сколько угодно одинаковых элементов, но выступать они будут как один. То есть множество не может содержать одни и те же элементы в нескольких вариантах. Предположим, что мы записали множество {7, 9, 7, 11, 7}. В этом множестве элемент 7 повторяется несколько раз, но мы его будем рассматривать как один. Поэтому наше множество будет {7, 9, 11}.
Рассмотрим два множества: {а, b, с} и {b, а, с}. Эти множества состоят из одних и тех же элементов, хотя они записаны в разном порядке. Такие множества называются равными. Итак, два множества равны, если содержат одни и те же элементы.
2. П е р е с е ч е н и е м н о ж е с т в.
Рассмотрим два множества: А = {1, 2, 3, 4, 5, 6} и В = {5, 6, 7, 8, 9}. Составим новое множество С, в которое запишем общие элементы А и В. Общими у них являются элементы 5 и 6, значит, С = {5, 6}. Множество С является пересечением множеств А и В, обозначается так:
