В зависимости от выбора рабочей точки на проходной динамической характеристике транзистора различают три основных режима работы усилительного каскада: А, В и АВ.
Режимы работы УПТ А, В и АВ
В зависимости от выбора рабочей точки на проходной динамической характеристике транзистора различают три основных режима работы усилительного каскада: А, В и АВ.
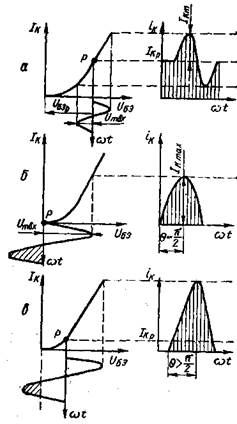
Режим А: для работы каскада на базу подается такое напряжение смещения, чтобы рабочая точка Р, определяющая исходное состояние схемы при отсутствии входного сигнала, располагалась примерно на середине прямолинейного участка характеристики (рис. 13.15, а). В этом режиме UБЭр ≥ Um BX, а IKp > IKт . Поэтому в режиме A при подаче на вход каскада синусоидального напряжения в выходной цепи будет протекать ток, изменяющийся по синусоидальному закону. Это обусловливает минимальные нелинейные искажения сигнала. Однако этот режим является наименее экономичным и к.п.д. усилительного каскада в режиме А составляет лишь 20− 30%.
Рис. 13.15. Графики, иллюстрирующие работу усилительного каскада в режимах:
а– класса А; б–класса В; в–класса АВ
В режиме В (рис. 13.15, б) рабочая точка выбирается так, чтобы ток покоя был равен нулю. При подаче на вход сигнала ток в выходной цепи каскада протекает лишь в течение половины периода изменения напряжения сигнала. В этом случае выходной ток имеет 
форму импульсов с углом отсечки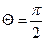 
(углом отсечки принято называть половину той части периода, в течение которого проходит ток). Режим В характеризуется высоким к. п. д. усилителя (60-70%), так как постоянная составляющая выходного тока значительно меньше, чем в режиме А1. Однако режим В характеризуется большими нелинейными искажениями сигнала.
Режим АВ является промежуточным между режимами А и В (рис. 13.15, в)2.
Основы булевой алгебры
В основе математического описания работы вычислительных устройств лежит алгебра логики или булева алгебра.
Переменные и их функции могут принимать только 2 значения: «0» и «1». Над переменными могут производиться 3 действия:
- логическое сложение – функция И;
- логическое умножение – функция ИЛИ;
- логическое отрицание – функция НЕ
Логическая функция И – КОНЪЮНКЦИЯ- У=Х1 Х2.
Логическая функция ИЛИ – ДИЗЪЮНКЦИЯ- У=Х1vХ2.
Логическая функция НЕ – ИНВЕРСИЯ- У=Х.
А также: 1. И-НЕ – отрицание конъюнкции (операция Шефера – У=Х1 Х2);
2. ИЛИ-НЕ – отрицание дизъюнкции (операция Пирса – У=Х1vХ2).
Составляется также ТАБЛИЦА ИСТИННОСТИ:
| Х1 | Х2 | У | ||||
| ИЛИ | И | НЕ | И-НЕ | ИЛИ-НЕ | ||
| 0 0 1 1 | 0 1 0 1 | 0 1 1 1 | 0 0 0 1 | 1 1 0 0 | 1 1 1 0 | 1 0 0 0 |
Согласно ЕСКД они обозначаются так: