Применение широкополосных сигналов
Широкополосные системы находят практическое применение прежде всего для борьбы с замираниями в коротковолновых радиоканалах. В узкополосных системах, когда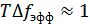 
, длительность сигнала на выходе оптимального фильтра определяется интервалом корреляции сигнала
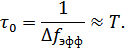
Это означает, что при многолучевом распространении сигналы отдельных лучей, имеющих различные запаздывания, взаимно перекрываются (рис. 12.10, а), и разделить их практически невозможно.
На рис. 12.10, а) в качестве примера показаны огибающие напряжений на выходе согласованных фильтров при приеме двоичной последовательности 1011, когда сигнал является узкополосным и образован тремя лучами. Сплошными линиями показаны напряжения, соответствующие первому лучу, а пунктиром – напряжения, относящиеся к двум другим лучам. Из рисунка видно, что в момент отсчета максимального значения напряжения первого луча на противоположном фильтре существуют напряжения от других лучей. Происходит перекрытие сигналов, поступающих на решающее устройство одновременно с двух фильтров, и вероятность ошибки резко возрастает. Это обстоятельство ограничивает скорость передачи информации, т.к. для нормальной работы необходимо, чтобы длительность элемента сообщения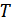 
во много раз превышала максимальное запаздывание лучей относительно друг друга 
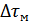. Иная картина наблюдается в случае широкополосных сигналов, когда
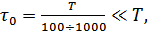(рис. 12.10, б). Сигналы на выходе в этом случае не перекрываются, если 
. Это условие является менее жестким, и поэтому представляется возможным значительно повысить скорость работы по сравнению с узкополосными системами. Разделение лучей в широкополосных системах устраняет интерференцию между ними, т.е. одну из причин, вызывающих замирания сигналов. Более того, здесь можно посредством дополнительной обработки сложить все разделенные лучи и таким образом использовать многолучевость для повышения помехоустойчивости.
Рисунок 12.10. Отклики на выходе согласованных фильтров в двоичной системе:
а) многолучевых узкополосных;
б) широкополосных сигналов
Другой важной областью применения шумоподобных сигналов является многоадресные системы связи с вызовом произвольного абонента. В такой системе связи обеспечивается связь по радио речевыми сигналами в одном частотном канале без помощи центрального коммутатора подобно обычной телефонной связи. Каждому абоненту присваивается определенный адрес в виде двоичной кодовой комбинации. Передача адреса осуществляется так, что «единице» соответствует одна псевдослучайная последовательность, а «нулю» – другая. Для вызова абонента кроме адреса вызываемого абонента обычно передается и собственный адрес, что упрощает процесс установления двусторонней связи.
Низкочастотный речевой сигнал (после приема адресов) квантуется и передается в дискретном виде также с помощью псевдослучайных последовательностей аналогично передаче адресов. Система связи обеспечивает хорошую скрытность передачи и прием речевых сигналов при малых отношениях сигнал/шум.
Известные в настоящее время многоадресные системы связи обеспечивают связь нескольких тысяч абонентов в одном частотном канале; причем одновременно может состояться несколько десятков переговоров.
Применение шумоподобных сигналов в радиолокации явилось своего рода технической революцией, т.к. появился реальный путь разрешения противоречия между требованием большой дальности радиолокатора и его разрешающей способности (точности). При обычных сигналах для повышения точности необходимо уменьшение длительности импульса, а для сохранения дальности необходимо сохранение той же энергии импульса, т.е. соответствующего увеличения пиковой мощности передатчиков. Мощность же радиолокационных передатчиков уже достигает десятков тысяч киловатт, т.е. практического предела.
Зондирующие импульсы большой длительности в виде шумоподобных сигналов позволяют получить сигнал с большой энергией и хорошей разрешающей способностью благодаря сжатию сигнала в приемнике (основной максимум корреляционной функции остается узким) при тех же пиковых мощностях передатчика. Кроме рекуррентных n-последовательностей в радиолокации нашли применение и другие псевдослучайные последовательности (коды Баркера, Шермана, Френка и др.), автокорреляционные функции которых имеют один большой максимум при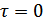 
и малый уровень боковых лепестков.
Наконец, необходимо отметить возможность использования шумоподобных сигналов для повышения эффективности систем связи в ряде областей, например, в дальней космической связи. Имея набор шумоподобных сигналов с хорошими корреляционными свойствами, можно построить эффективную систему связи, в которой осуществляется прием сигналов в целом (один из наиболее помехоустойчивых методов приема). В космической связи это позволило уменьшить мощность бортовых передатчиков и увеличить дальность связи.
Заключение
Фундаментальными работами В.А. Котельникова и К. Шеннона было положено начало современной теории связи. В трудах советских российских и зарубежных ученых эта теория получила дальнейшее развитие.
Современная система теории электрической связи использует термины и методы из различных научных областей, и прежде всего – математики, физики, теории цепей, вычислительной техники. Основные понятия, используемые в курсе ТЭС: математические модели сообщений, сигналов, помех и каналов в системах связи.
Следует подчеркнуть, что ТЭС достигла в последнее время значительных успехов в связи с переходам к цифровым методам передачи различных сообщений и цифровой обработки сигналов на большей части тракта передачи при широком использовании микропроцессорной техники. На этой основе создаются интегральные цифровые сети, в которых достигается не только наиболее полная интеграция по видам связи и услуг, но и интеграция технических средств передачи, обработки, коммутации и контроля.
Информация как совокупность знаний является главнейшим стратегическим ресурсом общества, его основным богатством, определяющим уровень развития общества, его цивилизованность.
Проблемы информатизации предъявляют высокие требования к технике связи. Для техники связи это прежде всего: высокие скорости (порядка гигабит и более в секунду), малые вероятности ошибок (порядка 10–10...10–11), большие дальности передачи (100 млн. км и более в системах космической связи), малые массы и низкое потребление энергии аппаратурой.
Успешное решение отмеченных выше проблем – ответственная задача ученых и инженеров, работающих в области связи. Часть этой работы, несомненно, ляжет на плечи тех, которым в первую очередь адресуется эта книга – нынешним студентам Университетов Телекоммуникации и Информатики.
Список литературы
1. В.С. Андреев. Теория нелинейных электрических цепей. Учеб. пособие для вузов. – М.: Радио и связь, 1982. – 280 с.
2. С.И. Баскаков. Радиотехнические цепи и сигналы. Учебник для вузов. – М.: Высшая школа, 1988 – 448 с.
3. Л.Е. Варакин. Системы связи с шумоподобными сигналами. – М.: Радио и связь, 1985. – 384 с.
4. А.Д. Витерби, Д.К. Омура. Принципы цифровой связи и кодирования / Пер. с англ. под ред. К.Ш. Зигангирова. – М.: Радио и связь, 1982. – 526 с.
5. Дж. Возенкрафт, И. Джекобс. Теоретические основы техники связи / Пер. с англ. под ред. Р.Л. Добрушина. – М.: Мир, 1969. – 640 с.
6. А.Г. Зюко. Помехоустойчивость и эффективность систем связи. – М.: Связь, 1972. – 352 с.
7. А.Г. Зюко, Д.Д. Кловский, М.В. Назаров, Л.М. Финк. Теория передачи сигналов. учебник для вузов. – М.: Радио и связь, 1986. – 302 с.
8. В.А. Котельников. Теория потенциальной помехоустойчивости. – М.–Л.: Госэнергоиздат, 1956. – 152 с.
9. Б.Р. Левин. Теоретические основы статистической радиотехники. – М.: Радио и связь, 1989. – 653 с.
10. А.А. Макаров, Л.А. Чиненков. Основы теории информации. Учеб. пособие. Новосибирск, 1998. – 24 с.
11. А.А. Макаров, Л.А. Чиненков. Основы теории помехоустойчивости дискретных сигналов. Учеб. пособие. Новосибирск, 1997. – 26 с.
12. Л.М. Финк. Теория передачи дискретных сообщений. – М.: Сов. радио, 1970. – 727 с.
13. А.А. Харкевич. Избранные труды. Т.З. Теория информации.Опознание образов. – М.: Наука, 1972. – 524 с.
14. К. Шеннон. Работы по информации и кибернетике / Пер. с англ. под ред. Н.А. Железнова. – М.: ИЛ. 1963. – 829 с.
Основные обозначения
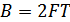– база сигнала
, 
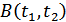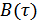– функция корреляции процесса (сигнала)
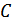– пропускная способность канала (бит/символ или бит/отсчет)
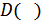– дисперсия случайного процесса
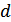– расстояние между сигнальными точками, расстояние по Хэмингу между двоичными последовательностями, минимальное расстояние по Хэмингу между комбинациями линейного блочного кода.
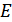– энергия принимаемого сигнала
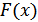– функция распределения вероятностей (ФРВ); интегральная функция распределения
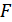– полоса частот сигнала (канала)
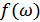– частота
, 
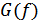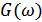– спектральная плотность мощности
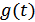– импульсная характеристика линейной цепи
, 
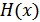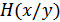– энтропия и условная энтропия дискретной случайной величины (дискретного источника)
, 
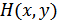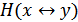– энтропия совместная и взаимная
, 
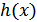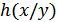– дифференциальная энтропия и условная дифференциальная энтропия непрерывного источника
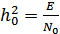– отношение энергии элемента сигнала на входе демодулятора к спектральной плотности мощности белого шума
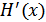– производительность дискретного источника
, 
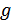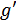– выигрыш и обобщенный выигрыш системы модуляции
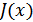– количественная мера информации
, 
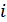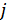– знаки мнимой единицы
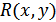– скорость передачи информации от 
к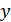 
, 
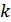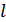– объем алфавита дискретного источника
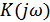– комплексный коэффициент передачи
, 
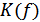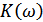– амплитудно-частотная характеристика (АЧХ)
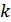– число информационных символов в цифровой комбинации
– длина (общее число символов) кодовой комбинации
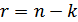– число проверочных (корректирующих) символов в кодовых комбинациях блочного кода
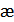– избыточность дискретного источника
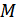– индекс угловой модуляции
, 
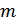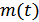– математическое ожидание случайной величины (процесса)
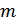– основание кода, коэффициент глубины амплитудной модуляции
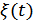– случайная аддитивная помеха, реализация случайного процесса (СП)
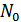– спектральная плотность мощности «белого» шума
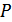– средняя мощность сигнала
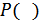– вероятность события, указанного в скобках
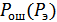– вероятность ошибочного приема символа
, 
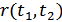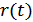– нормированная функция корреляции, коэффициент корреляции
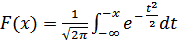– интеграл Лапласа
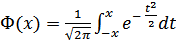– интеграл вероятности
– случайный сигнал на входе приемника (детектора) без учета аддитивных помех
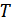– длительность интервала
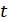– текущее время
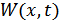– одномерная функция плотности вероятности (ФПВ) случайного процесса
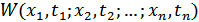– n-мерная ФПВ
– реализация суммы сигнала и аддитивной помехи на входе приемника (детектора)
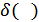– дельта-функция
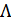– отношение правдоподобия
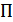– пик-фактор сообщения или сигнала (отношение максимального значения к среднеквадратическому)
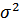– дисперсия случайной величины (процесса)
– интервал между двумя сечениями
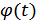– фаза сигнала или угловой модуляции
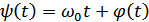– полная фаза сигнала
, 
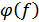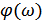– фазо-частотная характеристика (ФЧХ)
, 
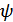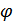– фазовый сдвиг, фаза сигнала
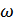– угловая частота
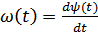– мгновенная частота сигнала
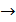– переход
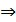– отсюда следует
Точка сверху означает комплексное выражение
Знак * сверху выражения означает комплексное сопряжение
Прямая черта над символом или формулой означает статистическое усреднение по (ансамблю), волнистая – по времени
Знак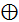 
означает сложение по модулю 2
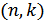– обозначение линейного блочного кода длины с 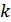информационными символами
Оглавление
Предисловие. 3
Часть I. Теория нелинейных электрических цепей. 4
1. Задачи курса ТЭС.. 4
2. Сигналы связи. 8
2.1. Формирование и преобразование сигналов. Кодирование и декодирование. Модуляция и демодуляция. 8