Формирование шумоподобных сигналов
Для того, чтобы широкополосные сигналы могли быть использованы в системах передачи сообщений, они должны удовлетворять ряду дополнительных требований:
1. Набор шумоподобных сигналов должен быть таким, чтобы их взаимокорреляционные функции были близки к нулю, а корреляционная функция каждого отдельного сигнала имела один достаточно узкий максимум значительной амплитуды.
2. Сигналы должны обладать минимальным пик-фактором, т.е. огибающая сигналов должны быть близка к постоянной. Т.к. пиковая мощность сигнала ограничивается техническими характеристиками передатчика, то максимальной энергией будут обладать сигналы с постоянной огибающей и мощностью, равной пиковой мощности передатчика. Как известно, потенциальная помехоустойчивость при аддитивном шуме зависит только от энергии сигнала и спектральной плотности шума.
3. Возможность независимого воспроизведения сигналов в приемнике.
4. Возможность синхронизации принимаемых и передаваемых сигналов.
Рассмотрим некоторые шумоподобные сигналы, методы их генерации и приема.
В первых широкополосных системах в качестве сигналов использовались реализации шума достаточно большой длительности. Если спектр источника шума равномерен по полосе частот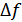 
, то при достаточно большой длительности реализации 
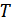интервал корреляции 
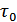обратно пропорционален 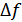, а боковые максимумы автокорреляционной функции достаточно малы. Такие сигналы позволяют построить систему связи с разделением сигналов, временные сдвиги между которыми превышают интервал корреляции .
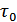Однако использование в качестве сигналов образцов реального шума связано с преодолением значительных трудностей. Т.к. в этом случае должен использоваться корреляционный метод приема, то в приемнике должны храниться точные копии применяемых для передачи сигналов, либо эти опорные сигналы должны поступать по специальному каналу связи из пункта передачи. В связи с этим возникает необходимость точной синхронизации, которую трудно осуществить, когда сигналы имеют вид реализаций естественного шума. При применении взаимокорреляционных (относительных) методов приема, не требующих специального опорного сигнала, снижается помехоустойчивость систем связи. Отметим также, что при передаче реализаций шума плохо используется мощность передатчика, т.к. огибающая высокочастотного колебания, модулированного шумом, имеет значительный пик-фактор, т.е. далека от постоянной.
Ввиду указанных недостатков сигналы в виде реализаций шума не нашли в настоящее время широкого применения. Из возможных способов построения систем, использующих такие сигналы, можно указать систему с модуляцией расстояния между максимумами корреляционной функции (корреляционная функция реализации шума в этом случае должна иметь по крайней мере два максимума, рис. 12.7).
Рисунок 12.7. Использование сигналов в виде реализаций шума
Одним из распространенных методов получения широкополосных сигналов является глубокая модуляция частоты несущего колебания по линейному закону. При этом частота в пределах длительности сигнала 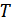изменяется по закону
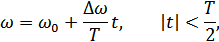
где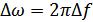 
– девиация частоты,
– несущая частота.
На выходе фильтра, оптимального для такого широкополосного сигнала, получается сигнал (корреляционная функция) вида
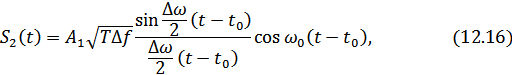
где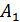 
– амплитуда сигнала на выходе фильтра.
В сигнале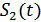 
уже нет частотной модуляции, и его огибающая имеет вид:
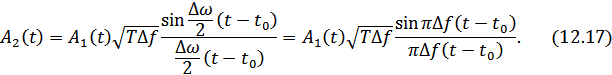
Недостатком сигнала с линейной частотной модуляцией является довольно высокий уровень боковых лепестков огибающей корреляционной функции (12.17), достигающий 22% основного максимума. Для улучшения формы выходного сигнала в приемнике иногда применяется не оптимальный фильтр, а квазиоптимальный, обеспечивающий подавление боковых лепестков выходного сигнала (например, вместо фильтра с прямоугольной огибающей амплитудно-частотной характеристики, оптимального для сигнала с линейной изменяющейся частотой, используется фильтр с колоколообразной огибающей).
Сигналы с линейной частотной модуляцией можно независимо генерировать на приемной и передающей станциях и проще синхронизировать, чем реализации шума. Определенные трудности возникают здесь при необходимости получения набора сигналов с хорошими корреляционными свойствами.
Наибольшее распространение получили шумоподобные сигналы, образующиеся при модуляции гармонического высокочастотного колебания некоторой псевдослучайной последовательностью. Чаще всего используются двоичные кодовые последовательности, т.к. их генерирование и прием наиболее просто осуществляется технически. Такие сигналы имеют, как правило, минимальный пик-фактор.
Псевдослучайной последовательностью называется регулярная последовательность кодовых символов длиной (значностью) 
, корреляционные свойства которой близки к корреляционным свойствам дискретной случайной последовательности (клиппированного шума).
Число символов различного вида в такой последовательности (0 или 1 в двоичной) примерно одинаково, а число групп одинаковых символов убывает с увеличением количества символов в группе.
В настоящее время известно большое число псевдослучайных последовательностей, обладающих хорошими корреляционными свойствами. Рассмотрим свойства и способ формирования так называемых двоичных n -последовательностей. Автокорреляционная функция n-последовательности может быть определена следующим образом:
1. Для периодически повторяющейся последовательности
где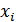 
, 
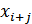– значения элементов кодовой последовательности (в двоичной последовательности это либо «1» либо «–1»), причем
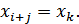
2. Для непериодической последовательности
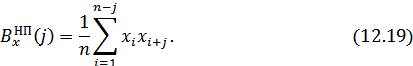
Например, периодическая двоичная последовательность вида (1, –1, –1, 1) имеет корреляционную функцию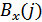 
(рис. 12.8), у которой
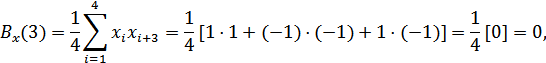
Рисунок 12.8. а) временная характеристика функции 
;
б) функция корреляции периодической последовательности;
в) функция корреляции непериодической последовательности
Если последовательность непериодическая, корреляционная функция имеет значения
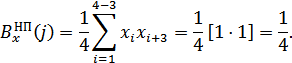
Псевдослучайной последовательностью обычно называют только такие последовательности, для которых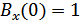 
, а 
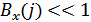при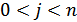 
. Примером такой последовательности является последовательность (1, 1, 1, –1). Значения ее корреляционной функции при 
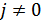равны 0.
Наиболее распространены и хорошо изучены такие псевдослучайные n-последовательности, которые представляют собой последовательности максимальной длины регистра сдвига (линейные рекуррентные последовательности, в которых операции сложения и умножения производятся по модулю 2). Такие последовательности имеют длину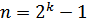 
и корреляционную функцию вида
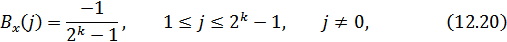
где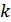 
– число двоичных элементов в регистре сдвига, используемом для формирования данной n-последовательности.
Энергетический спектр периодической n-последовательности определяется выражением
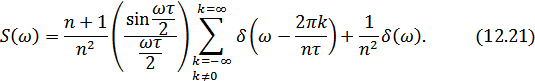
т.е. является дискретным с частотами, кратными основной части
повторения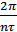 
, где 
– длительность одного элемента последовательности.
Рекуррентные n -последовательности нашли широкое применение в системах связи вследствие простоты их формирования. Для этого используется двоичный (бинарный) регистр сдвига. Двоичный регистр сдвига из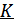 
элементов – это устройство, содержащее 
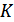последовательно соединенных двоичных ячеек (например, триггеров), которые в моменты времени, определяемые тактовым генератором, могут изменять свое состояние на обратное (ячейки могут иметь два состояния: либо 1, либо –1 или 0). Причем под действием тактового импульса состояния предыдущих ячеек переходят в последующие (рис. 12.9). Кроме того, определенные ячейки через специальные логические устройства (обычно это сумматоры по модулю 2) связаны со входом регистра, в результате чего регистр сдвига из 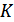ячеек может генерировать последовательность с периодом , не превосходящим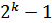 
. Для каждого 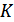существует n-последовательность и она псевдослучайна, т.е. удовлетворяет условиям:
1. Число «единиц» и «нулей» в последовательности отличается не более, чем на единицу, и чем больше длина группы одинаковых символов, тем меньше частота их появления в последовательности.
2. Корреляционная функция 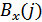имеет единственный максимум, равный 1, при 
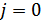, а при 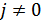не превышает величины 
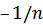и величины 
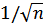, когда последовательность не периодическая.
На рис. 12.9 приведена схема для формирования n-последовательности с периодом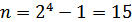 
.
Если начальное состояние регистра 1000 (т.е единица записана только в первую ячейку), то на выходе будет наблюдаться последовательность 000 100 110 101 111. Можно убедиться, что эта последовательность является псевдослучайной (удовлетворяет вышесказанным условиям). Правила выбора обратных связей в регистре сдвига (на рис. 12.9 третья и четвертая ячейка связаны с первой через сумматор по модулю 2) известны в теории линейных рекуррентных последовательностей.
Рисунок 12.9. Структурная схема формирования последовательности 