11.2. Классификация корректирующих кодов

Дата: 2025-06-02; Просмотры: 16

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

В настоящее время известно большое количество корректирующих кодов, отличающихся как принципами построения, так и основными характеристиками. Рассмотрим их простейшую классификацию (рис. 11.2).

Рисунок 11.2. Классификация корректирующих кодов

Все известные в настоящее время коды могут быть разделены на две большие группы:

1) блочные;

2) непрерывные.

1. Блочные коды характеризуются тем, что последовательность передаваемых символов разделена на блоки. Операции кодирования и декодирования в каждом блоке производятся отдельно.

2. Отличительной особенностью непрерывных кодов является то, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.

3. Разновидностями как блочных, так и непрерывных кодов являются разделимые и неразделимые коды. В разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточными и служат исключительно для коррекции ошибок. В неразделимых кодах такое разделение символов провести невозможно.

Наиболее многочисленный класс разделимых кодов составляют линейные коды. Основная их особенность состоит в том, что контрольные символы образуются как линейные комбинации информационных символов.

4. В свою очередь, линейные коды могут быть разбиты на два подкласса: систематические и несистематические. Все двоичные систематические коды являются групповыми. Групповые характеризуются принадлежностью кодовых комбинаций к группе, обладающей тем свойством, что сумма по модулю два для любой пары комбинаций снова дает комбинацию, принадлежащую этой группе. Линейные коды, которые не могут быть отнесены к подклассу систематических, называются несистематическими.

В вертикальных прямоугольниках представлены некоторые конкретные коды, рассматриваемые далее.

11.3. Обнаруживающая и исправляющая способность кодов

Для лучшего понимания сущности обнаружения и исправления ошибок воспользуемся пространственными представлениями.

Для обнаружения ошибок все пространство кодовых слов подразделяется на два подпространства – разрешенных и запрещенных комбинаций (кодовых слов).

Рисунок 11.3. Сущность обнаружения ошибок

Следует заметить, что если из-за воздействия помех одна разрешенная кодовая комбинация преобразуется в другую разрешенную кодовую комбинацию, то такая ошибка, хотя она и присутствует, обнаружена не будет.

Для исправления ошибок все пространство кодовых слов разбивается на 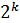подпространств (непересекающихся).

Рисунок 11.4. Сущность исправления ошибок

В каждом подпространстве находится одна разрешенная комбинация (обозначена кружком «○») и некоторое количество запрещенных из общего количества 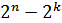(обозначенных точками «•»). Все запрещенные кодовые комбинации распределяются по 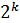подпространствам по принципу «близости» к разрешенной кодовой комбинации данного подпространства (т.е. отличающиеся в одном или двух и т.д. знаках от разрешенной кодовой комбинации).

Исправление ошибок производится в два этапа:

1. Определяется кодовое расстояние между пришедшей кодовой комбинацией и всеми разрешенными кодовыми комбинациями.

2. Решение принимается в пользу той разрешенной кодовой комбинции, для которой кодовое расстояние будет наименьшим (т.е. реализуется критерий идеального наблюдателя).

Для получения некоторых количественных соотношений рассмотрим две комбинаци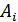и и 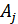, расстояние между которыми условно обозначено на рис. 11.5, а, где промежуточные комбинации отличаются друг от друга одним символом.

Рисунок 11.5. Иллюстрация для определения кодовых расстояний при обнаружении и исправлении ошибок

В общем случае некоторая пара разрешенных комбинаци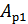й и 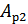, разделенных кодовым расстоянием 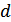, изображена на прямой рис. 11.5, б, где точками указаны запрещенные комбинации. Для того, чтобы в результате ошибки комбинация 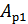преобразовалась в другую разрешенную комбинацию 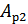, должно исказиться 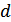символов. При искажении меньшего числа символов комбинация 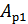перейдет в запрещенную комбинацию и ошибка будет обнаружена. Отсюда следует, что ошибка всегда обнаруживается, если ее кратность, т.е. число искаженных символов в кодовой комбинации

Если 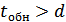, то некоторые ошибки также обнаруживаются. Однако полной гарантии обнаружения ошибок здесь нет, т.к. ошибочная комбинация в этом случае может совпасть с какой-либо разрешенной комбинацией. Минимальное кодовое расстояние, при котором обнаруживаются любые одиночные ошибки, .

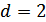Процедура исправления ошибок в процессе декодирования сводится к определению переданной комбинации по известной принятой. Расстояние между переданной разрешенной комбинацией и принятой запрещенной комбинацией 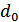равно кратности ошибок 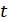. Если ошибки в символах комбинации происходят независимо относительно друг друга, то вероятность искажения некоторых 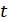символов в n-значной комбинации будет равна:

где 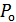– вероятность искажения одного символа.

Т.к. обычно 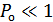, то вероятность многократных ошибок уменьшается с увеличением их кратности, при этом более вероятные меньше расстояния 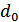. В этих условиях исправление ошибок может производиться по следующему правилу. Если принята запрещенная комбинация, то считается переданной ближайшая разрешенная комбинация. Например, пусть образовалась запрещенная комбинация 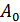(рис. 11.5, б), тогда принимается решение, что была передана комбинация 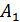. Это правило декодирования для указанного распределения ошибок является оптимальным, т.к. оно обеспечивает исправление максимального числа ошибок. В общем случае оптимальное правило декодирования зависит от распределения ошибок (их статистики). Напомним, что аналогичное правило используется в теории потенциальной помехоустойчивости при оптимальном приеме дискретных сигналов, когда решение сводится к выбору того переданного сигнала, который в наименьшей степени отличается от принятого. Нетрудно определить, что при таком правиле декодирования будут исправляться все ошибки кратности:

Минимальное значение 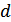, при котором еще возможно исправление любых одиночных, равно 3.

Возможно также построение таких кодов, в которых часть ошибок исправляется, а часть только обнаруживается. Так, в соответствии с рис. 11.5, в, ошибки кратности 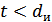исправляются, а ошибки, кратность которых лежит в пределах 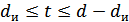, только обнаруживаются. Что касается ошибок, кратность которых сосредоточена в пределах 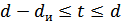, то они обнаруживаются, однако при их исправлении принимается ошибочное решение – считается переданной комбинацией 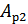вместо 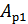или наоборот.

Существуют двоичные системы связи, в которых решающее устройство выдает, кроме обычных символов 0 и 1, еще так называемый символ стирания θ. Этот символ соответствует приему сомнительных сигналов, когда затруднительно принять определенное решение в отношении того, какой из символов, 0 или 1, был передан. Принятый символ в этом случае стирается. Однако при использовании корректирующего кода возможно восстановление стертых символов.

Если в кодовой комбинации число символов 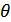оказалась равным 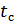, причем

а остальные символы приняты без ошибок, то такая комбинация полностью восстанавливается.

Корректирующая способность кода возрастает с увеличением 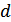. При фиксированном числе разрешенных комбинаций 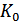увеличение 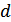возможно лишь за счет роста количества запрещенных комбинаций

что, в свою очередь, требует избыточного числа символов 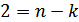, где 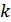– количество символов в комбинации кода без избыточности. Можно ввести понятие избыточности кода и количественно определить ее:

При независимых ошибках вероятность определенного сочетания 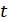ошибочных символов в n-значной кодовой комбинации выражается формулой (11.2), а количество всевозможных сочетаний 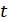ошибочных символов в комбинации зависит от ее длины и определяется известной формулой числа сочетаний:

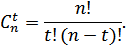
Отсюда полная вероятность ошибки кратности 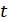, учитывающая все сочетания ошибочных символов, равняется:

Используя (11.7), можно записать формулу, определяющую вероятность отсутствия ошибок в кодовой комбинации, т.е. вероятность правильного приема:

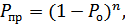
и вероятность правильного корректирования ошибок:

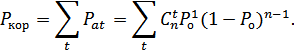
Здесь суммирование производится по всем значениям кратности ошибок 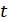, которые обнаруживаются и исправляются. Таким образом, вероятность необнаруженных ошибок равна:

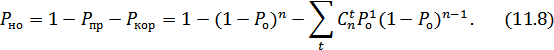
Вероятность 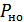, избыточность 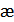и число символов являются основными характеристиками корректирующего кода, определяющими, насколько удается повысить помехоустойчивость передачи дискретных сообщений и какой ценой это достигается.

11.4. Простейшие корректирующие коды

Порядок рассмотрения:

1) название;

2) принцип обнаружения ошибок;

3) код коэффициента обнаружения;

4) вероятность ошибки;

5) вероятность необнаруженной ошибки;

6) избыточность кода.

1. 1) Код с проверкой на четность.

К информационным символам добавляется один проверочный так, чтобы число единиц было четным, например:

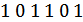
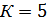
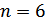
2) Обнаруживает все ошибки нечетной кратности. Принцип обнаружения – проверка на прочность.

3) .

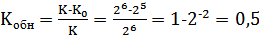4) .

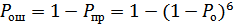Если ошибка двукратная, четырехкратная, шестикратная – ошибка не обнаруживается.

5) .

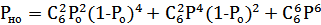Вероятность Вероятность Вероятность

2-хкратной 4-хкратной 6-тикратной

ошибки ошибки ошибки

6) 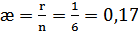. Код разделимый, блочный.

2. 1) Код с постоянным весом.

Вес – число единиц в кодовой комбинации длиной . Код 3:4 (3 единицы, 4 нуля).

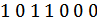
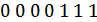
2) Обнаруживает все ошибки нечетной кратности и 50% ошибок четной кратности. Не обнаруживаются такие ошибки четной кратности, когда количество искаженных единиц равно количеству искаженных нулей.

3) .

,

,

.

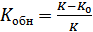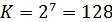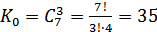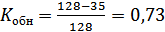4) .

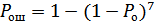5) .

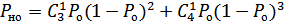Вероятность Вероятность

искажения 1 искажения 0

Ошибки не обнаруживаются, если произойдет 2^х кратная ошибка, т.е. 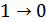и одновременно 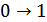(или 2 ед 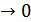и 2 нуля 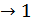; или 3 ед 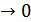, 3 нуля ).

.

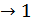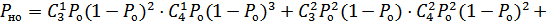
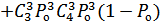6) Избыточность кода:

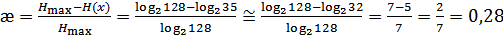
(в приближенной оценке вместо 35 взяли 32).

Код блочный, неразделимый, систематический.

3. 1) Инверсный код.

Имеет 5 информационных и 5 проверочных символов ( , ).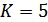

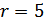2) Если в информационной части четное число единиц, то проверочные символы образуются повторением информационной части.

инф. пров.

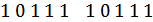
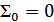
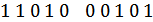
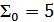
Если нечетное число единиц в информационной части, то проверочные образуются из информационных путем инвертирования. В противном случае обнаруживающая способность кода будет хуже.

3) .

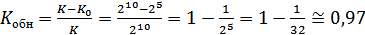Код обнаруживает все одиночные, двойные, тройные ошибки и все ошибки нечетной кратности.

Не обнаруживаются ошибки 4-й кратности, когда в проверочной части искажены те же элементы, что и в информационной.

4) .

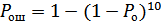5) .

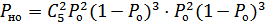Вероятность Вероятность

искажения 2-х элементов искажения тех же элементов

информационной части проверочной части

6) .

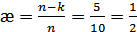Код блочный, разделимый, систематический, 50% информационной части повторяется.

4. Цепной код (непрерывный или рекуррентный).

Строится так, чтобы число проверочных символов равнялось числу информационных, т.е. 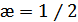, и они чередуются:

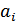– информационные символы;

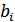– проверочные символы.

; ,

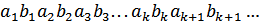
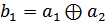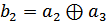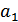и 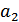– различные информационные символы,

символ « 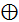» означает сложение по модулю 2.

При ошибочном приеме некоторого корректирующего символа 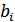соотношение (11.1) не выполняется для .

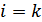В случае ошибочного приема информационного символа 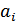соотношение (11.1) не будет выполняться при двух значениях 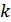: 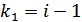и .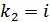

Отсюда правило исправления ошибок при декодировании. В принятой кодовой последовательности для каждого 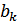проверяется соотношение (11.1). Если оно оказалось невыполненным при двух значениях 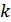( 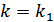и 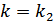) и при этом 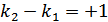, информационный элемент 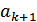заменяется на противоположный.

Избыточность кода 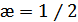, что позволяет исправлять все ошибки, если они возникают достаточно редко. Он обеспечивает правильное декодирование, когда между двумя ошибочно принятыми символами имеется не менее трех правильно принятых. При этом учитываются как информационные, так и корректирующие символы.

11.5. Сложные систематические коды

1. Систематический ( 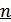, 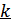) код.

Представляет собой набор n-разрядных кодовых комбинаций, в которых 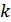разрядов (обычно первые) представляют собой результат примитивного кодирования сообщения. Они называются информационными разрядами. Остальные 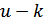разрядов образуются по определенным правилам из информационных, они называются проверочными (корректирующими) и служат для обнаружения и исправления ошибок. Так, например, код (7,4) – это код, в котором семиэлементная кодовая комбинация содержит 4 информационных символа.

Другими словами, процесс кодирования сообщения можно представить последовательностью двух процессов – сначала производится кодирование равномерным n-разрядным кодом без внесения избыточности, а затем к каждой кодовой комбинации приписываются сформированные по определенным правилам 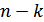корректирующих разрядов.

Приведем пример построения кода (7,4). Как видно из обозначения, 4 разряда кодовой комбинации заняты информационными символами. Обозначение их 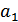, , 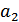, 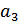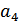. Остальные 3 разряда заняты корректирующими символами, которые обозначим 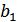, , 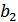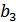. Символы 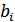определяются уравнениями:

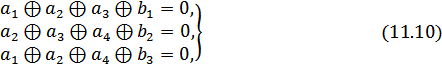
где сложение производится по модулю 2. Так, например, если информационными символами являются 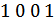, то корректирующими должны быть 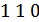. В таком коде .

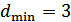Отсюда следует, что, используя такой код, можно всегда обнаруживать ошибку, если ошибочно принято не более двух символов в комбинации, либо исправлять ошибку, если ошибочно принят один символ.

С целью обнаружения ошибок принятая кодовая комбинация подвергается проверке на удовлетворение уравнениям, используемых для формирования корректирующих символов (11.10), т.е. проверкой на четность, поскольку ( ).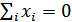

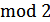Если хотя бы одно из этих уравнений не удовлетворено, то принятая комбинация не принадлежит к числу разрешенных, и, следовательно, в процессе передачи произошла ошибка.

При исправлении ошибок необходимо учитывать, какие из уравнений не удовлетворены, и руководствоваться специальными правилами:

1. Например, если из уравнений (11.10) два оказываются справедливыми, а одно не удовлетворяется, то ошибочно принятым следует считать один из корректирующих символов и принятая комбинация может быть декодирована по информационным символам без каких-либо исправлений.

2. Если не удовлетворены первые два уравнения, то подлежит исправлению (замене 0 на 1 или 1 на 0) символ 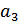, который входит в оба этих уравнения. Если не удовлетворены 1 и 3 уравнения, то исправлению подлежит символ 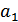. Если не удовлетворены 2-е и 3-е уравнение, исправлению подлежит символ 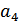. Наконец, если все три уравнения не удовлетворены, то исправлению подлежит символ 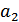. Если в кодовой комбинации ошибочно приняты два или более символов, то такая комбинация не будет правильно декодирована.

Групповой код ( , 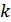) можно однозначно определить, задав всего лишь 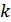входящих в него линейных независимых комбинаций. Они образуют производящую матрицу 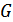, имеющую 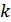строк и столбцов. По ней можно построить все остальные кодовые комбинации, складывая (по разряду и по модулю 2) попарно по три, по четыре и т.д. строки производящей матрицы.

В частности, складывая любую строку саму с собой, получим нулевую комбинацию (состоящую из нулей).

Для кода ( , 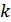) производящая матрица может быть записана в таком виде:

r

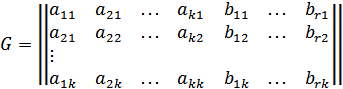
n

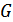– производящая матрица.

Путем разрядного суммирования можно получить любую кодовую комбинацию.

Для декодирования с обнаружением или исправлением ошибок в памяти декодера достаточно хранить проверочную матрицу 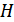, содержащую 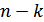строк и столбцов. В каждой строке этой матрицы единицы находятся в тех разрядах, которые входят в соответствующее проверочное уравнение (11.10). В нашем примере:

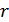
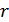(единичная матрица)

2. Циклические коды (систематический блочный код).

Разрешенные комбинации циклического кода можно вычислить последовательно, применяя две операции: циклическую перестановку и суммирование по модулю 2. Циклическая перестановка менее трудоемкая, и это обстоятельство полезно использовать для упрощения процесса вычислений. Расширим производящий момент кода (7,4) до семи членов, применяя нулевые коэффициенты:

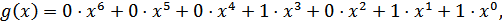
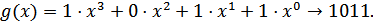
Запишем первую комбинацию: .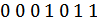

Применив шесть раз операцию циклической перестановки, можно записать следующие шесть комбинаций. Дальнейшее применение перестановки теряет смысл (они будут приводить к повторению уже имеющихся). Просуммируем по модулю два любые две комбинации из уже имеющихся. Получим комбинацию, содержащую четыре единицы и три нуля. Следующие шесть комбинаций получаются в результате шестикратной циклической перестановки ее элементов.

Чтобы получить пятнадцатую комбинацию, нужно найти среди ранее полученных четырнадцати любую пару взаимно противоположных и просуммировать их по модулю 2 ( 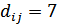). Получим комбинацию, состоящую из семи единиц. Шестнадцатую комбинацию (состоящую из 7 нулей) не используют, ее можно вычислить, прибавив к любой из имеющихся комбинаций ее же по модулю 2.

Рассмотрим еще один способ нахождения разрешенных кодовых комбинаций, который широко применяется на практике.

Пусть 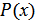– информационный полином, наивысшая степень которого 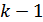(состоит из 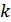элементов). Умножим каждый информационный многочлен на выравнивающий полином 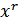(в нашем случае 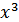), что соответствует приписыванию справа 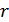нулей. Разделим полученный результат на производящий полином 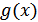, операция деления выполняется по модулю 2.

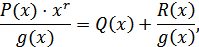
где 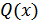– частное от деления, нас не интересует,

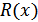– остаток от деления.

Если остаток от деления добавить к 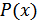, то получим комбинацию, делящуюся без остатка на производящий полином, т.е. разрешенную комбинацию данного кода.

Пример:

, ,

, .

, .

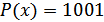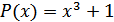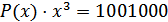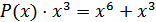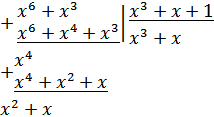
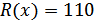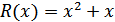Разрешенная кодовая комбинация имеет вид:

, .

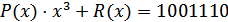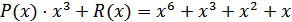В приемнике (декодере) принятая кодовая комбинация делится на производящий полином. При нулевом остатке комбинация принята верно, либо содержит необнаруженную ошибку; остаток от деления указывает, что комбинация принята с обнаруженной ошибкой. По виду остатка может быть определен искаженный элемент в информационной части принятой комбинации (формируется так называемый синдром).

12. Системы передачи сообщений с обратной связью

12.1. Классификация систем с обратной связью

Все системы передачи сообщений могут быть разделены на две группы: прямые системы передачи и системы с обратной связью.

В прямых системах связи повышение достоверности передачи сообщений достигается выбором соответствующего способа передачи и приема сигналов, а также применением корректирующих кодов, исправляющих ошибки.

В последние годы довольно широкое распространение получили системы, в которых для повышения достоверности (помехоустойчивости) передачи сообщений используются обратные каналы связи. Если система связи является двухсторонней (сообщения передаются в оба направления), то каждый из каналов связи может использоваться для повышения помехоустойчивости обратного для него канала методами обратной связи.

Рисунок 12.1. Варианты построения систем с обратной связью

Обратной связью могут быть охвачены различные части системы передачи. Три основных варианта показаны на рис. 12.1.

1. В первом варианте обратная связь охватывает и контролирует только линию связи. По обратному каналу передаются только сведения о качестве принимаемого сигнала. Роль обратной связи при этом состоит в том, чтобы в соответствии с состоянием сигнала на входе приемника измерить параметры передаваемых сигналов: мощность передатчика, скорость передачи сигналов, или вообще прекратить передачу при особо неблагоприятных условиях (например, в системах метеорной связи и т.д.).

2. Обратная связь включена после первого решающего устройства. По обратному каналу передаются сведения о принятых решениях: например, после демодулятора приемника или после регистрации элементов кодовых комбинаций.

3. Обратная связь охватывает всю систему, включая кодирующее устройство передатчика и декодирующее (второе решающее) устройство приемника. По обратному каналу связи передаются сведения о принимаемых кодовых комбинациях.

В системах с обратной связью (варианты 2 и 3) на основании поступающих по обратному каналу сведений производится либо повторная передача сомнительных сигналов, либо передача данных о необходимых исправлениях. Следовательно, если в прямых системах связи избыточность, необходимая для обнаружения и исправления ошибок, должна быть введена в каждую передаваемую кодовую комбинацию, то в системах с обратной связью избыточность, необходимая для исправления ошибки, вводится только тогда, когда эта ошибка обнаружена. Поэтому прямые системы связи иногда называют системами с постоянной избыточностью, а системы с обратной связью – системами с переменной избыточностью. В прямых системах связи постоянная избыточность обусловлена избыточностью применяемого для исправления ошибок корректирующего кода. В системах с обратной связью для исправления ошибок используется только переменная избыточность (неправильно принятые сообщения повторяются); обнаружение же ошибок может осуществляться как за счет постоянной избыточности, т.е. применения обнаруживающего ошибки корректирующего кода, так и без постоянной избыточности, когда ошибки обнаруживаются путем анализа характера искажений принимаемых сигналов (поэлементная проверка).

Известно, что для обнаружения ошибок всегда требуется значительно меньшая постоянная избыточность, чем для исправления ошибок. Поэтому системы с обратной связью могут работать с меньшей удельной избыточностью (избыточностью, отнесенной к одной исправленной ошибке), чем прямые системы связи и, таким образом, являются статистически более согласованными.

Необходимость в специальном канале связи технически усложняет системы с обратной связью. Кроме того, эффективность систем с обратной связью несколько снижается за счет ошибок, возникающих в канале обратной связи. Для исправления ошибок в сигналах обратной связи, как правило, используется канал передачи сообщений, который для этих сигналов уже является каналом обратной связи. В то же время применение обратной связи не требует применения сложных методов кодирования сообщений для повышения достоверности передачи, а, следовательно, по сравнению с прямыми системами связи с исправлением ошибок упрощается техническая реализация кодирующих и декодирующих устройств.

По способу использования канала обратной связи системы с обратной связью (второй и третий вариант) могут быть разделены на:

- системы с информационной обратной связью (ИОС) или системы со сравнением;

- системы с решающей обратной связью (РОС) или системы с переспросом.

Информационная обратная связь

В системах с информационной обратной связью приемная сторона по обратному каналу только информирует передатчик, какое сообщение принято или каким определяющими признаками оно обладает. На основании этой информации передатчик либо подтверждает правильность принятых сообщений, либо вносит те или иные изменения в процесс передачи сообщения, например, повторяет ошибочно принятые сообщения, изменяет применяемый код и т.д.

Простейшим по реализации методом ИОС является метод полной обратной ретрансляции принятых сообщений. Передатчик сравнивает ретранслированные по обратному каналу кодовые комбинации сообщения с фактически переданными. В случае их несовпадения передается сигнал для стирания принятой комбинации, а затем повторно передается нужная комбинация. В качестве сигнала для стирания используется специальная кодовая комбинация, не применяемая для передачи сообщений. В такой системе связи ошибка не исправляется только в том случае, если ошибка в прямом канале компенсируется ошибками в канале обратной связи. Вероятность такой ошибки равна 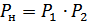, где 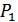– вероятность ошибки в прямом канале, 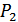– вероятность ошибки в канале обратной связи.

Особой опасностью в системах с ИОС является искажение или ложный прием сигнала стирания. В первом случае сигнал стирания принимается как комбинация сообщения и повторно принимается повторяемая кодовая комбинация, ложно принятая за сигнал стирания, и стирается предшествующая кодовая комбинация сообщения. Чтобы уменьшить вероятность такого рода групповых ошибок, сигнал стирания кодируется так, чтобы обеспечить как можно большее кодовое расстояние по отношению к кодовым комбинациям сообщения.

Другим недостатком метода полной ретрансляции является большая нагрузка канала обратной связи, т.к. сообщения должны быть полностью переданы как по прямому, так и по обратному каналам. Поэтому более совершенным методом ИОС является метод передачи по каналу обратной связи только определяющих признаков (квитанций) группы принятых комбинаций сообщения. Квитанция всегда значительно короче группы комбинаций сообщения, т.к. она несет только признаки, отличающие данную группу комбинаций сообщения от соседних групп. Принцип исправления ошибок при передаче укороченных квитанций тот же, что и при полной ретрансляции. Принятая квитанция сравнивается с хранящейся в передатчике, и в зависимости от результатов сравнения либо передается следующая группа комбинаций сообщения, либо передается сигнал стирания и повторяется искаженная группа комбинаций сообщения. Уменьшение нагрузки обратного канала связи имеет значение особенно в том случае, когда сообщения передаются как по прямому, так и по обратному каналам. При этом для обратного канала прямой канал используется в качестве канала обратной связи. Естественно, что чем длиннее квитанции, тем меньше средняя скорость передачи сообщений по этим каналам связи.

Решающая обратная связь

В системах с решающей обратной связью (с переспросом) решение об отсутствии ошибок в принятой комбинации сообщения осуществляется приемником.

Обнаружение ошибок в системах с переспросом осуществляется либо путем проверки принятых комбинаций в процессе декодирования, либо путем поэлементной проверки элементов принятой комбинации в первом решающем устройстве. Довольно часто оба способа обнаружения ошибок используются совместно.

Для обнаружения ошибок путем проверки принимаемых кодовых комбинаций передаваемые сообщения кодируются корректирующим кодом (кодом с избыточностью). Выбор кода производится в соответствии со свойствами канала связи. Кодовая комбинаций сообщения считается принятой правильно, если она относится к разрешенной комбинации данного корректирующего кода и неправильно принятой, если она принадлежит к неразрешенным комбинациям.

Для обнаружения ошибок путем поэлементной проверки принимаемых сигналов применение корректирующего кода не обязательно. Одним из возможных способов поэлементной проверки является способ сравнения принимаемой элементарной посылки с контрольным импульсом (рис. 12.2). Длительность и амплитуда контрольного импульса выбирается в соответствии с параметрами канала связи и требуемой помехоустойчивостью.

Рисунок 12.2. Способ сравнения принимаемой посылки с контрольным импульсом

Контрольный импульс с амплитудой 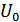и длительностью 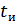располагается в средней части принимаемых элементарных посылок. Ошибка считается обнаруженной, если огибающая сигнала попадает в зону, ограниченную контрольным импульсом.

Поэлементная проверка может применяться как самостоятельно, так и в сочетании с корректирующими кодами. В последнем случае обеспечивается значительное усиление эффективности корректирующих кодов.

В случае обнаружения ошибки по каналу обратной связи передается сигнал переспроса, для которого используется специальная кодовая комбинация. По этому сигналу передатчик повторяет неправильно принятую комбинацию, которой обычно предшествует сигнал предупреждения о повторении. Применение системы с переспросом особенно целесообразно при организации дуплексной связи, когда в каждом направлении передаются сообщения, а при необходимости передача сообщений прекращается и посылается сигнал переспроса.

Вероятность ошибочного приема комбинации сообщения в системах с переспросом определяется обнаруживающей способностью используемого корректирующего кода. Как и в системе с информационной обратной связью, в системах с переспросом возможны групповые ошибки, возникающие при ложном приеме сигнала переспроса или пропуске этого сигнала. Поэтому к кодированию сигнала переспроса предъявляются особо жесткие требования.

В заключение необходимо отметить одно обстоятельство, относящееся как к системам связи с ИОС, так и к системам связи с РОС. Т.к. сигналы по каналам связи распространяются с конечной скоростью, то после передачи очередной комбинации сообщения сигнал обратной связи, подтверждающий или отрицающий прием данной комбинации, поступает через значительный промежуток времени. Чтобы не было потери времени, передатчик передает другие комбинации сообщения. В скоростных системах связи до получения сигнала обратной связи может быть передано несколько десятков кодовых комбинаций. Как правило, в этом случае трудно однозначно определить, к какой комбинации сообщения относится сигнал стирания (ИОС) или сигнал переспроса (РОС). Поэтому, например, в системах связи с переспросом передатчик по сигналу переспроса должен повторять не одну, а значительно большее число ранее переданных кодовых комбинаций с учетом времени замедления в канале связи так, чтобы ошибочно принятая комбинация обязательно оказалась в числе повторяемых. Передатчик, а иногда и приемник должны содержать специальные запоминающие устройства, в которых хранятся комбинации сообщения до получения соответствующих сигналов обратной связи.

Время распространения сигналов по кольцу обратной связи (приемник – линия связи – передатчик – линия связи – приемник) называют периодом или циклом повторения. Чем больше период повторения системы связи, тем больше времени затрачивается на исправление обнаруженной ошибки.