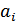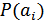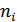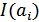Пусть источник сообщений вырабатывает четыре сообщения , и с вероятностями , , .

Дата: 2025-06-02; Просмотры: 16

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Все сообщения выписываются в кодовую таблицу (табл. 10.1) в порядке убывания их вероятностей. Затем они разделяются на две группы так, чтобы суммы их вероятностей по возможности были одинаковы. В данном примере в первую группу входит сообщение 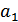с вероятностью 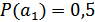и во вторую – сообщения 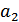, 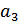и 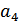с суммарной вероятностью, также равной 0,5.

Комбинациям, которые соответствуют сообщениям первой группы, присваивается в качестве первого символа кода 0, а комбинациям второй группы – 1. Каждая из двух групп опять делится на две группы с применением того же правила присвоения символов 0 и 1. В идеальном случае после первого деления вероятности каждой группы должны быть равны 0,5, после второго деления 0,25 и т.д. Процесс деления продолжается до тех пор, пока в группах не останется по одному сообщению.

Таблица 10.1 – Кодовая таблица.

		Группы			Комби- нации
		I	II	III
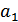
	0,5}	0			0	1	1
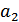
	0,25	1}	0		10	2	2
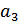
	0,125	1	1}	0	110	3	3
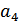
	0,125	1	1}	1	111	3	3

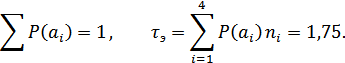
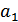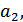
Для сравнения рассмотрим кодирование тех же четырех сообщени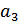й , и 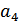с применением обычного равномерного кода. Количество комбинаций при этом 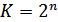, где – число элементов в комбинации. Так как 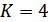, то 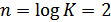, длительность кодовой комбинации .

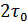В рассматриваемом примере средняя длительность комбинаций благодаря примененному статическому кодированию уменьшалось в 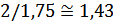раза. Во столько же раз увеличилась и производительность источника (10.25).

10.10. Энтропия непрерывного источника и ее свойства

Энтропия дискретного сигнала определяется выражением (10.2). Для непрерывной случайной величины воспользуемся этим же выражением, заменив вероятность 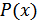на 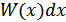. В результате получим:

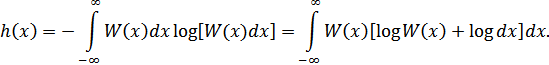
Но логарифм бесконечно малой величины ( 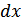) равен минус бесконечности, в результате чего получаем:

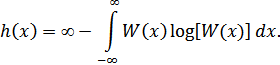
Таким образом, энтропия непрерывной случайной величины бесконечно велика. Но т.к. в последнем выражении первое слагаемое ( 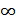) от величины или от 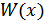не зависит, при определении энтропии непрерывной величины это слагаемое отбрасывают, учитывая только втрое слагаемое (некоторую «добавку» к бесконечности). Эта добавочная энтропия определяется формулой:

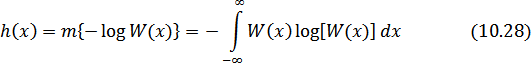
и называется дифференциальной энтропией непрерывной случайной величины. В дальнейшем слово «дифференциальное» в определении энтропии будем иногда отпускать.

Как и для дискретных сообщений, существуют следующие разновидности дифференциальной энтропии непрерывной величины:

1. Условная энтропия случайной величины 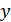относительно случайной величины :

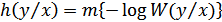
или

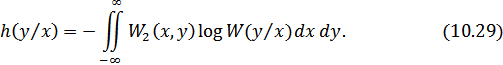
2. Совместная энтропия двух непрерывных случайных величин:

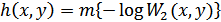
или

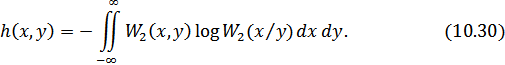
Для независимых и .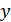

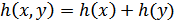Для совместной дифференциальной энтропии непрерывной случайной величины справедливы соотношения (10.18) и (10.19).

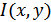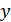3. Взаимная информация , содержащаяся в двух непрерывных сигналах и , определяется формулой (10.21).

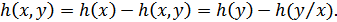
Для независимых и .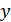

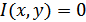4. Если случайная величина ограничена в объеме 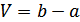, то ее дифференциальная энтропия максимальна при равномерном законе распределения этой величины:

Рисунок 10.5. Равномерный закон распределения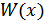

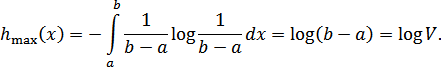
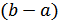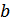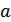Т.к. эта величина зависит только от разности и не зависит от абсолютных величин и , то 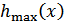не зависит от мат. ожидания случайной величины .

5. Если случайная величина не ограничена в объеме (т.е. может изменяться в пределах от 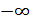до 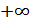), а ограничена только по мощности, то дифференциальная энтропия максимальна в случае гауссовского закона распределения этой величины. Определим этот максимум.

В соответствии с (10.28):

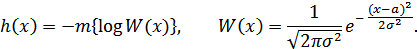
Отсюда:

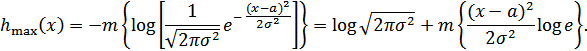
Но математическое ожидание 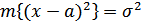, отсюда получим:

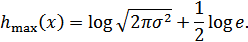
Или окончательно:

Следовательно, энтропия не зависит только от мощности 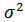. Эта важная формула будет использоваться позднее для определения пропускной способности непрерывного канала связи.

Заметим, что, как и ранее, 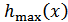не зависит от математического ожидания 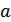случайной величины . Это важное свойство энтропии. Оно объясняется тем, что мат. ожидание является неслучайной величиной.

10.11. Пропускная способность непрерывного канала связи

Если – сигнал на входе канала связи, а 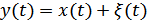– сигнал на его выходе ( 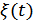– аддитивная помеха), то скорость передачи информации по непрерывному каналу связи будет определяться выражением (10.24), в котором величину надо заменить на :

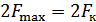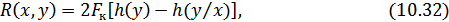
где, как и ранее 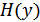– это энтропия выходного сигнала, 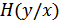– энтропия шума (почему она так называется, будет видно из дальнейшего изложения).

Пропускная способность равна максимально возможной скорости передачи по каналу связи, когда источник сигнала полностью согласован с характеристиками канала связи:

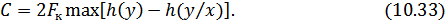
Максимум 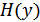достигается в случае гауссовского закона распределения величины 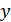. При этом:

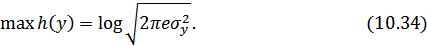
При учете влияния помехи необходимо рассматривать наихудший случай, когда помеха распределена также по гауссовскому закону. Условная вероятность 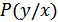– это фактически плотность вероятности 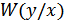случайной величины 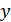при якобы известном заранее значении , хотя величина является случайной. Но, т.к. 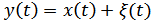, можно записать:

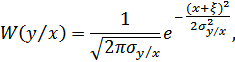
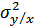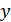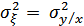где – дисперсия величины при известном , т.е. дисперсия помехи . Определим условную энтропию :

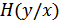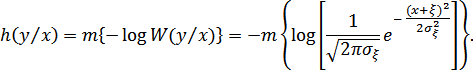
В этом выражении предполагается, что известно заранее. Таким образом, величина в приведенном выражении является математическим ожиданием величины 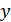. Однако известно, что энтропия непрерывного случайного процесса от мат. ожидания не зависит. Тогда получаем:

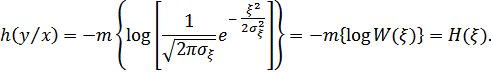
Отсюда видно, почему условная энтропия 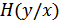называется энтропией шума.

Для гауссовского закона распределения помехи максимальное значение энтропии шума в соответствии (10.31) будет равно

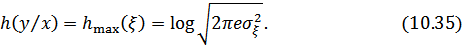
Подставляя (10.34) и (10.35) в (10.33), получаем:

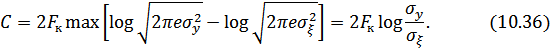
Перенося число 2 под знак логарифма, получим:

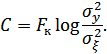
В этом выражении 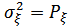– мощность помехи, а 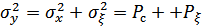, где 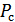– мощность сигнала на выходе канала связи. С учетом этого получаем окончательную формулу для вычисления пропускной способности непрерывного канала связи (формулу Шеннона):

В заключение отметим следующее.

Для достижения скорости передачи информации по непрерывному каналу связи, близкой к пропускной способности канала связи, сигнал по статической структуре должен быть близок к флуктуационной помехе (белому шуму) с гауссовским законом распределения.

10.12. Эпсилон-энтропия источника непрерывных сообщений

Сигнал на выходе источника (И) непрерывных сообщений (например, микрофона, телефона, датчика температуры и пр.) представляет собой непрерывный случайный процесс, энтропия которого в любом из сечений в общем случае равна бесконечности, как это было показано в разделе 10.10. Такое количество информации не может быть передано по реальному каналу связи, пропускная способность которого всегда ограничена. Это и не нужно, т.к. скорость восприятия информации любым потребителем на выходе канала всегда ограничена его физическими возможностями. Поэтому непрерывный сигнал на выходе канала связи даже без помех отличается от сигнала на входе, т.к. содержит не всю информацию о нем (причем под каналом связи можно понимать любое преобразование одного ансамбля сигналов в другое: модуляцию, усиление, дискретизацию и пр.). Уже преобразование непрерывного сообщения в сигнал соответствующим устройством (микрофоном или другим датчиком сигнала) связано с потерей части информации, а сигнал отображает сообщении лишь с некоторой точностью:

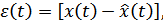
где – сигнал на входе преобразователя,

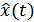– сигнал на выходе преобразователя (Пр) или оценка входного сигнала преобразователем, который всегда представляет собой некоторое решающее устройство, работающее по определенному правилу и заданному критерию качества.

Рисунок 10.6.

Критерий качества, как известно, определяется потребителем информации. Например, среднеквадратическое отклонение:

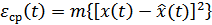
или дисперсия ошибки

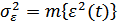
Эпсилон-энтропией 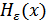(ε-энтропией) называется минимальное количество информации, которое должно содержаться в выходном сигнале 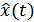о входном сигнале , чтобы этот сигнал можно было восстановить с заданной точностью .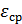

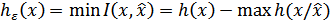
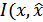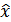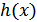где ) – взаимная информация и ,

и 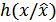– соответственно дифференциальная энтропия сигнала и условная энтропия , когда 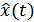известно; 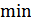и 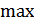берутся по всевозможным условным ФПВ .

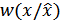В общем случае, когда сигнал (или сообщение) является гауссовским с дисперсией 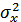, ошибка 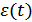также является гауссовской с дисперсией 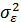, а с учетом аддитивного характера ошибки 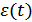условная энтропия 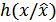полностью определяется дифференциальной энтропией 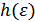. Соответственно, .

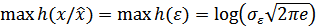Тогда 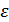– энтропия одного сечения гауссовского источника ( 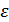– энтропия одного отсчета).

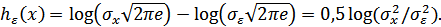
Величина 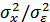показывает отношение мощности (дисперсии) сигнала к мощности (дисперсии) ошибки, при котором среднеквадратическое отклонение сигналов и 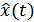не превышает .

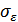Следовательно, производительность источника непрерывных сообщений можно определить как количество информации, которое необходимо передавать в единицу времени, чтобы восстановить сообщение с заданной точностью.

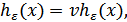
где 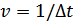– скорость передачи отсчетов на выходе источника,

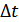– интервал между отсчетами.

Для стационарного сигнала с ограниченным спектром 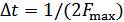, тогда .

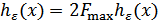Кроме того, если источник является гауссовским, то

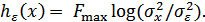
Количество информации, выдаваемое гауссовским источником за время 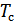, равно 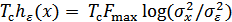, что совпадает с формулой для объема сигнала, когда динамический диапазон сигнала

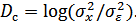
Это значит, что объем сигнала на выходе источника равен количеству информации, которое содержится в сигнале, для его воспроизведения с заданной точностью.

Для канала с пропускной способностью 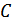, на выходе которого подключен источник с производительностью 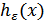, теорема К. Шеннона для канала с шумами принимает вид:

Если при заданном критерии точности источника (например, 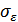) его эпсилон-производительность меньше пропускной способности канала 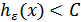, то существует способ кодирования (преобразования сигнала), при котором неточность воспроизведения сколь угодно близка к 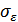; при 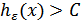такого способа не существует.

Теорема К. Шеннона определяет предельные возможности согласования источника непрерывных сообщений с каналом связи. Практически это достигается применением помехоустойчивых видов модуляции и кодирования.

11. Корректирующие коды

11.1. Принципы помехоустойчивого кодирования. Кодовое расстояние

В теории помехоустойчивого кодирования важным является вопрос об использовании избыточности для корректирования возникающих при передаче ошибок. Здесь удобно рассмотреть блочные коды, в которых всегда имеется возможность выделить отдельные кодовые комбинации. Напомним, что для равномерных кодов число возможных комбинаций равно 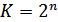, где – значимость кода. В обычном не корректирующем коде без избыточности число комбинаций K выбирается равным числу сообщений алфавита источника 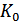, и все комбинации используются для передачи информации. Корректирующие коды строятся так, чтобы число комбинаций 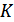превышало число сообщений источника 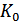. Однако в этом случае лишь 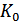комбинаций из общего числа используется для передачи информации. Эти комбинации называются разрешенными, а остальные 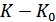комбинаций носят название запрещенных. На приемном конце на декодирующем устройстве известно, какие комбинации являются разрешенными и какие – запрещенными. Поэтому, если переданная разрешенная комбинация в результате ошибки преобразуется в некоторую запрещенную комбинацию, то такая ошибка будет обнаружена, а при определенных условиях исправлена. Известно, что ошибки, приводящие к образованию другой разрешенной комбинации, не образуются.

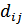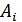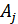Различие между комбинациями равномерного кода принято характеризовать расстоянием, равным числу символов, которыми отличаются комбинации одна от другой. Расстояние между двумя комбинациями и определяется количеством единиц в сумме этих комбинаций при сложении по модулю два.

Например:

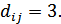
Для любого кода 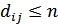минимальное расстояние между разрешенными комбинациями в данном коде называется кодовым расстоянием 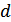, или расстоянием по Хэмингу.

Введем коэффициенты, характеризующие обнаруживающую и исправляющую способность кодов ( , ).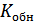

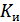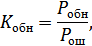
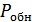– вероятность обнаружения ошибок,

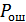– общая вероятность ошибок.

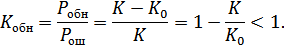
Принцип направления ошибок следующий. Мы разбиваем все множество комбинаций на ряд непересекающихся подпространство по количеству разрешенных комбинаций. Все запрещенные комбинации находятся в соответственных подпространствах разрешенных комбинаций. Если передавалась комбинация 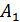и она незначительно исказилась помехами и попала в подпространство 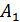, то считаем, что искажений не было. Коэффициент исправления:

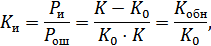
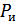– вероятность исправления ошибок.

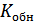в 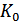раз больше .

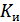Кратность ошибки – число искаженных элементов в одной комбинации. Если в комбинации 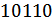искажено два элемента, то говорят, что ошибка двукратная. Кратность ошибок в значительной степени определяется каналом. Есть каналы, в которых ошибки случайны и независимы (в таких каналах с увеличением кратности ошибок вероятность увеличивается), а есть каналы, в которых ошибки пакетируются.

Рисунок 11.1. Модели каналов

а) с независимыми ошибками;

б) с кратными ошибками (пакетирование)

Для правильности выбора кода необходимо знать статистику ошибок в канале.