Здесь и – собственная энтропия источников x и y соответственно.
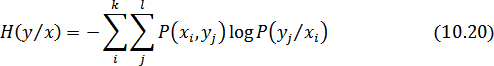
– условная энтропия источника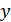 
относительно источника 
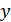. Она показывает, какую энтропию имеют сообщения , когда уже известно сообщение .
Если источники независимы, то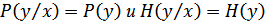 
. В этом случае
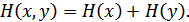
Если источники частично зависимы, то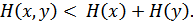 
Если источники полностью зависимы ( и 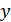содержат одну и ту же информацию), то 
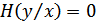и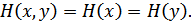 
10.7. Взаимная информация источников сообщений
На рис. 10.3 показана (условно) собственная энтропия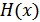 
и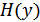 
, условные энтропи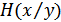и 
и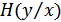 
и совместная энтропия 
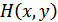. Из этого рисунка, в частности, следует соотношение (10.18) и (10.19).
Рисунок 10.3. Графическое представление собственных условных, совместных и взаимной энтропий
Заштрихованная часть рисунка называется взаимной информацией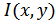 
. Она показывает, какое в среднем количество информации содержит сообщение о сообщении 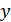(или наоборот). Как следует из рис. 10.3:
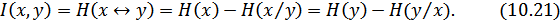
Рисунок 10.4. Графическое представление влияния потерь при передаче и приеме информации
Если сообщения и 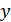полностью независимы, то взаимная информация отсутствует и 
.
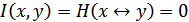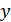Если сообщения и полностью зависимы ( и 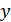содержат одну и ту же информацию), то 
.
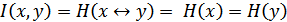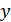Понятие взаимной информации очень широко используется в теории передачи информации. Требования к взаимной информации различны в зависимости от того, с какой информацией мы имеем дело. Например, если и – это сообщения, публикуемые различными газетами, то для получения возможно большей суммарной (совместной) информации взаимная (т.е. одинаковая в данном случае) информация должна быть минимальной. 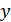Если же и – это сообщения на входе и на выходе канала связи с помехами, то для получения возможно большей информации ее получателем необходимо, чтобы взаимная информация была наибольшей. Тогда условная энтропия 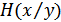– это потери информации в канале связи (надежность канала).
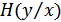– энтропия шума (помех), равная 
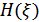, т.е. 
.
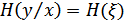10.8. Скорость передачи и пропускная способность канала связи
В дискретной системе связи при отсутствии помех информация на выходе канала связи (канала, передающего информацию) полностью совпадает с информацией на его входе, поэтому скорость передачи информации численно равна производительности источника сообщений:
При наличии помех часть информации оказывается меньшей, чем производительность источника. Одновременно в сообщении на выходе канала добавляется информация о помехах (рис. 10.4).
Рисунок 10.4. Влияние помех при передаче информации
Поэтому при наличии помех необходимо учитывать на выходе канала не всю информацию, даваемую источником, а только взаимную информацию.
На основании формулы (10.21) имеем:
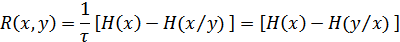
или
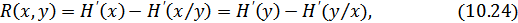
где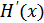 
– производительность источника,
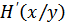– «ненадежность» канала (потери) в ед. времени,
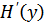– энтропия выходного сообщения в ед. времени,
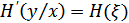– энтропия помех (шума) в ед. времени.
Пропускной способностью канала связи (канала передачи информации)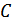 
называется максимально возможная скорость передачи информации по каналу:
Для достижения максимума учитываются все возможные источники на входе и все возможные способы кодирования.
Таким образом, пропускная способность канала связи равна максимальной производительности источника на входе канала, полностью согласованного с характеристиками этого канала, за вычетом потерь информации в канале из-за помех.
В канале без помех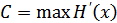 
, т.к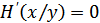 
. При использовании равномерного кода с основанием 
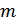, состоящего из 
элементов, длительностью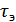 
, в канале без помех:
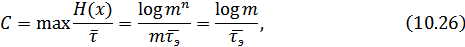
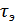– длительность элемента.
При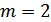 
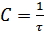бит/с.
Для эффективного использования пропускной способности канала необходимо его согласование с источником информации на входе. Такое согласование возможно как для каналов без помех, так и для каналов связи с помехами на основании двух теорем, доказанных К.Шенноном.
Первая теорема (для канала связи без помех):
Если источник сообщений имеет энтропию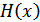 
(бит на символ), а канал связи – пропускную способность 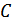(бит в секунду), то можно закодировать сообщение таким образом, чтобы передавать информацию по каналу со средней скоростью, сколь угодно близкой к величине 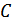, но не превзойти ее.
К.Шеннон предложил и метод такого кодирования, который получил название статического или оптимального кодирования. В дальнейшем идея такого кодирования была развита в работах Фано и Хаффмана и в настоящее время широко используется на практике для «сжатия сообщений».
Вторая теорема (для каналов связи с помехами):
Если пропускная способность канала равна 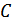, а производительность источника 
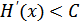, то путем соответствующего кодирования можно передавать информацию по каналу связи со скоростью, сколь угодно близкой к 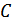, и с вероятностью ошибки, сколь угодно близкой к нулю. При 
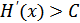такая передача невозможна.
К сожалению, теорема К.Шеннона для канала связи с шумом (помехами) указывает только на возможность такого кодирования, но не указывает способа построения соответствующего кода. Однако известно, что при приближению к пределу, устанавливаемому Теоремой Шеннона, резко возрастает время запаздывания сигнала в устройствах кодирования и декодирования из-за увеличения длины кодового слова . При этом вероятность эквивалентной ошибки на выходе канала стремится к величине
Очевидно, что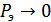 
, когда и 
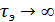, и, следовательно, имеет место «обмен» вероятности ошибки на скорость и задержку передачи.
10.9. Статическое кодирование дискретных сообщений
Кодирование по методу Шеннона-Фано-Хаффмана называется оптимальным, т.к. при этом повышается производительность дискретного источника, и статическим, т.к для реализации оптимального кодирования используются априорные вероятности появления на выходе источника каждого элемента сообщения (учитывается статистика сообщений).
Производительность и избыточность дискретного источника согласно определениям равны, соответственно:
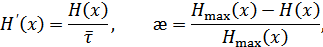
откуда получаем:
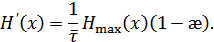
Из этой формулы видно, что для увеличения производительности нужно уменьшить избыточность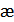 
и среднюю длительность сообщений 
.
Известно, что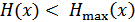 
, если априорные вероятности различных элементов сообщения различны ( 
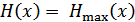при равной вероятности этих элементов). Но при неравной вероятности сообщений нужно применить оптимальное (статическое) кодирование, при котором уменьшается средняя длительность сообщений.
Идея такого кодирования заключается в том, что, применяя неравномерный неприводимый код, наиболее часто встречающиеся сообщения (буквы или слова) кодируются короткими комбинациями этого кода, а редко встречающиеся сообщения кодируются более длительными комбинациями.
Рассмотрим принципы оптимального кодирования на примере.