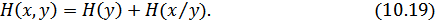В реальных условиях выбор конкретного сообщения производится с некоторой априорной вероятностью . Чем меньше эта вероятность, тем больше информации содержится в данном сообщении.
Вероятностный подход и положен в основу определения меры количества информации.
При определении количества информации исходят из следующих требований:
1. Количественная мера информации должна обладать свойством аддитивности: количество информации в нескольких независимых сообщениях должно равняться сумме количества информации в каждом сообщении.
2. Количество информации о достоверном событии (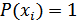 
) должно равняться нулю, так как такое сообщение не увеличивает наших знаний о данном объекте или явлении.
Указанным требованиям удовлетворяет логарифмическая мера, определяемая формулой:
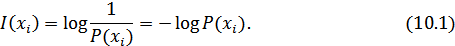
Чаще всего логарифм берется с основанием 2, реже – с основанием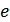 
:
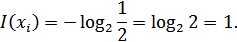
При применении натуральных логарифмов одну натуральную единицу информации содержит сообщение, вероятность выбора которого равняется 
:
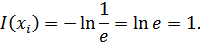
Учитывая, что в практике передачи и преобразования информации широко применяются двоичные символы, двоичная логика, двоичные источники сообщений и двоичные каналы передачи, наиболее часто используется двоичная единица информации (бит).
Хотя при определении количества информации под сообщениями можно понимать любые фразы или телеграфные сообщения, здесь элементарными сообщениями мы будем называть отдельные буквы или слова. При использовании двухуровневых дискретных сигналов, например, мы будем пользоваться элементарными двоичными сигналами «0», «1», считая их буквами.
Таким образом, алфавит двоичного источника состоит всего из двух букв, из которых можно строить длинные комбинации, называемые кодовыми словами.
10.2. Энтропия дискретного источника с независимым выбором сообщений
В теории информации чаще всего необходимо знать не количество информации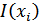 
, содержащееся в отдельном сообщении, а среднее количество информации в одном сообщении, создаваемом источником сообщений.
Если имеется ансамбль (полная группа) из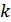 
сообщений 
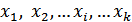с вероятностями 
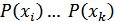, то среднее количество информации, приходящееся на одно сообщение и называемое энтропией источника сообщений 
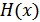, определяется формулой:
или
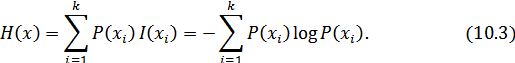
Размерность энтропии – количество единиц информации на символ. Энтропия характеризует источник сообщений с точки зрения неопределенности выбора того или другого сообщения.
Рассмотрим свойства энтропии:
1. Чем больше неопределенность выбора сообщений, тем больше энтропия. Неопределенность максимальна при равенстве вероятностей выбора каждого сообщения:
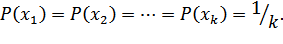
В этом случае
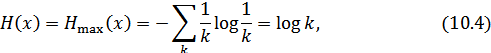
т.е. максимальная энтропия равна логарифму от объема алфавита). Например, при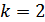 
(двоичный источник) 
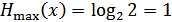бит.
2. Неопределенность минимальна, если одна из вероятностей равна единице, а остальные – нулю (выбирается всегда только одно заранее известное сообщение: например, одна буква):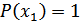 
; 
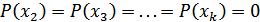. В этом случае 
.
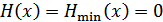Эти свойства энтропии иллюстрируются следующим образом.
Пусть имеется двоичный источник сообщений, т.е. осуществляется выбор из двух букв ( ):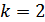 
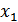и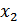 
, 
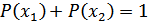. Тогда:
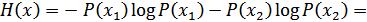
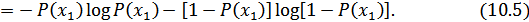
Зависимость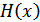 
от вероятностей выбора (10.5) для двоичного источника приведена на рис. 10.1.
Рисунок 10.1. Зависимость 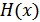от вероятности выбора для двоичного источника
3. Укрупним алфавит. Пусть на выходе двоичного источника имеется устройство, которое группирует буквы в слова из 
букв. Тогда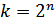 
слов (объем алфавита). В этом случае
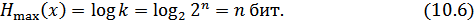
Таким образом, укрупнение алфавита привело к увеличению энтропии в раз, т.к. теперь уже слово включает в себя информацию букв двоичного источника. Тем самым доказывается свойство аддитивности энтропии.
4. Энтропия дискретного источника не может быть отрицательной.
Термин «энтропия» заимствован из термодинамики и применительно к технике связи предложен К. Шенноном, в трудах которого были заложены основы теории информации (математической теории связи).
10.3. Энтропия дискретного источника с зависимыми сообщениями
Ранее при определении энтропии предлагалось, что каждое сообщение (буква или слово) выбирается независимым образом. Рассмотрим более сложный случай, когда в источнике сообщений имеются корреляционные связи. В так называемом эргодическом источнике выбор очередной буквы сообщения зависит от каждого числа предшествующих букв. Математической моделью такого источника является Марковская цепь n-го порядка, у которой вероятность выбора очередной буквы зависит от предшествующих букв и не зависит от более ранних, что можно записать в виде следующего равенства:
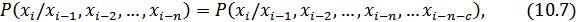
где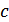 
– произвольное положительное число.
Если объем алфавита источника равен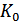 
, а число связанных букв, которое необходимо учитывать при определении вероятности очередной буквы, равно порядку источника , то каждой букве может предшествовать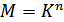 
различных сочетаний букв (состояний источника), влияющих на вероятность появления очередной буквы 
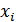на выходе источника. А вероятность появления в сообщении любой из 
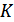возможных букв определяется условной вероятностью (10.7) с учетом предшествующих букв, т.е. с учетом 
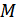возможных состояний. Эти состояния обозначим как 
.
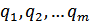Рассмотрим два простых примера.
Пример 1. Пусть имеется двоичный источник (объем алфавита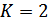 
), выдающий только буквы 
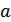и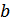 
; порядок источника 
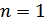. Тогда число состояний источника 
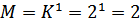(назовем эти состояния 
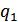и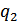 
). В этом случае вероятности появления букв 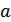и 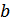будут определяться следующими условными вероятностями:
где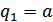 
– 1-ое состояние источника,
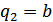– 2-ое состояние источника.
Т.е.
Пример 2. Пусть по-прежнему 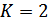(буквы 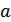и 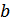), однако число связанных букв 
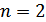. Тогда 
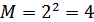(четыре возможных состояния): 
, 
, 
, 
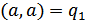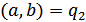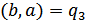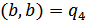. В этом случае имеем дело со следующими условными вероятностями:
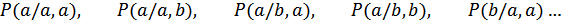
и т.д. Вероятности состояний определяются равенствами:
Энтропия эргодического дискретного источника определяется в два этапа:
1. Вычисляем энтропию источника в каждом из 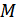состояний, считая эти состояния известными.
Для состояния :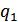
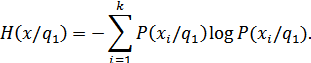
Для состояния :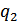
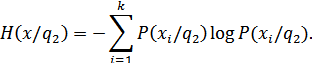
Для состояния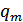 
:
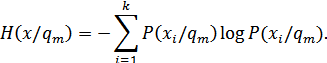
2. Далее находим 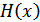путем усреднения по всем состояниям 
:
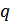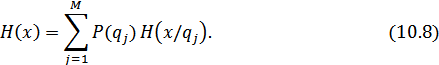
Окончательно получаем:
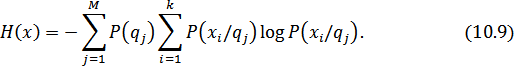
При наличии корреляционных связей между буквами в эргодическом источнике энтропия уменьшается, т.к при этом уменьшается неопределенность выбора букв, и в ряде случаев часть букв можно угадать по предыдущим или ближайшим буквам
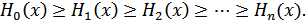
10.4. Избыточность источника
Как было показано ранее, энтропия максимальна при равновероятностном выборе элементов сообщений и отсутствии корреляционных связей. При неравномерном распределении вероятностей и при наличии корреляционных связей между буквами энтропия уменьшается.
Чем ближе энтропия источника к максимальной, тем рациональнее работает источник. Чтобы судить о том, насколько хорошо использует источник свой алфавит, вводят понятие избыточности источника сообщений:
или
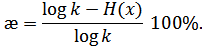
Наличие избыточности приводит к загрузке канала связи передачей лишних букв сообщений, которые не несут информации (их можно угадать и не передавая).
Однако преднамеренная избыточность в сообщениях иногда используется для повышения достоверности передачи информации – например, при помехоустойчивом кодировании в системах передачи информации с направлением ошибок (как и других) – около 50%. Благодаря избыточности облегчается понимание речи при наличии дефектов в произношении или при искажениях речевых сигналов в каналах связи.
10.5. Производительность источника
Производительность источника определяется количеством информации, передаваемой в единицу времени. Измеряется производительность количеством двоичных единиц информации (бит) в секунду. Если все элементы сообщения имеют одинаковую длительность 
, то производительность
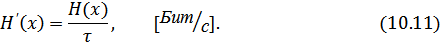
Если же различные элементы сообщения имеют разную длительность, то в приведенной формуле надо учитывать среднюю длительность 
, равную математическому ожиданию величины :
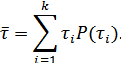
Однако в последней формуле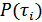 
можно заменить на 
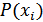(вероятность i-го сообщения), т.к. эти вероятности равны. В результате получаем:
А производительность источника будет равна:
Максимально возможная производительность дискретного источника равна:
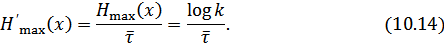
Для двоичного источника, имеющего одинаковую длительность элементов сообщения ( ,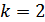 
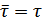), имеем
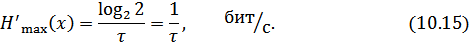
При укрупнении алфавита в слова по букв, когда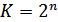 
, 
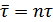, имеем:
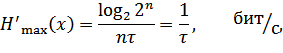
что совпадает с (10.15).
Таким образом, путем укрупнения алфавита увеличить производительность источника нельзя, так как в этом случае и энтропия, и длительность сообщения одновременно возрастают в одинаковое число раз ( ).
Увеличить производительность можно путем уменьшения длительности элементов сообщения, однако возможность эта ограничивается полосой пропускания канала связи. Поэтому производительность источника можно увеличить за счет более экономного использования полосы пропускания, например, путем применения сложных многоуровневых сигналов:
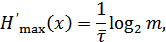
где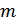 
– основание кода.
10.6. Совместная энтропия двух источников
Пусть имеется два дискретных источника с энтропиям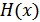и и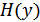 
и объемами алфавитов 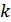и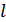 
(рис. 10.2).
Рисунок 10.2. Совместная энтропия двух источников
Объединим оба эти источника в один сложный источник и определим совместную энтропию. Элементарное сообщение на выходе системы содержит элементарное сообщение 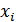и сообщение 
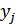. Алфавит сложной системы будет иметь объем 
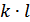, а энтропия будет равна
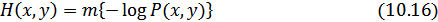
или
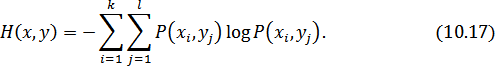
По теореме умножения вероятностей:
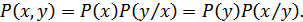
Подставляя эти соотношения в (10.16), получим:
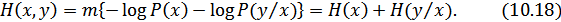
Аналогично можно получить:
