Вычислим вероятность ошибки в каналах с рэлеевскими замираниями.

Дата: 2025-06-02; Просмотры: 16

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Пусть 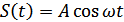, мощность помехи 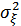. В случае рэлеевских замираний амплитуда сигнала 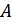является случайной величиной, и ее плотность вероятности равна:

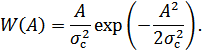
Здесь 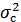– дисперсия замираний, характеризующая разброс амплитуд сигнала в процессе замираний.

Найдем .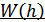

По определению

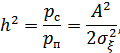
откуда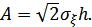

Здесь мы имеем дело с флуктуационной зависимостью 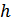от 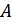. В соответствии с известным правилом определения плотностей вероятностей функционально-связанных величин, можно записать

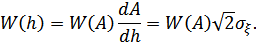
Преобразуя, получим:

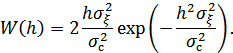
Введем понятие среднего значения отношения сигнал/шум:

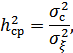
и подставив это выражение в предыдущее, получим:

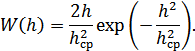
Отсюда видно, что величина 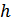подчиняется, как и величина 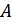, рэлеевскому закону распределения. Этого и следовало ожидать, т.к. 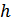и 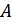связаны линейной зависимостью.

Теперь получим общее выражение для вероятности ошибки в канале с рэлеевскими замираниями:

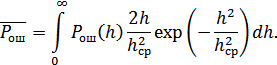
Рассмотрим несколько частных случаев.

1. Для приема сигналов ДЧМ некогерентным приемником получим:

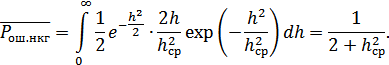
2. Для случая приема сигналов ДЧМ когерентным приемником получим:

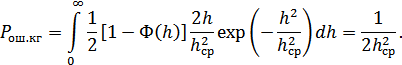
Сравнивая два последних выражения, видим, что, как и в каналах с постоянными параметрами, в каналах с замираниями переход от некогерентного приема к когерентному дает энергетический выигрыш, примерно равный двум. Если сравнить помехоустойчивость систем связи с каналами без замираний и системы с замираниями, то можно сделать вывод, что в каналах с замираниями для достижения малой вероятности ошибок мощность сигнала должна быть увеличена по сравнению с каналами без замираний в сотни раз. Поэтому в каналах с замираниями для уменьшения вероятности ошибок используют другие методы повышения помехоустойчи-вости (например, разнесенный прием). Кроме того, ошибки в таких каналах часто «пакетируются», т.е. встречаются интервалы времени, внутри которых вероятность ошибок резко увеличивается.

9.14. Прием сигналов ДОФМ

Дискретная фазовая модуляция обеспечивает наиболее высокую помехоустойчивость приема дискретных сигналов. Однако при практической реализации схемы приемника возникают трудности с получением опорного напряжения. Как видно из рис. 9.26, для получения опорного напряжения используется генератор, синхронизируемый входным сигналом.

Рисунок 9.26. Структурная схема приемника ДФМ (двухканальная)

Но схему можно упростить, если использовать один общий коррелятор (рис. 9.27).

Рисунок 9.27. Структурная схема приемника ДФМ (одноканальная)

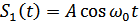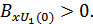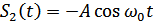Если содержит , на выходе интегратора имеем напряжение, равное Если же содержит сигнал , то на выходе интегратора имеем напряжение, равное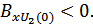

Напряжение на выходе интегратора сравнивается с пороговым напряжением, равным нулю, и в зависимости от результата сравнивания выдает сигналы или .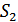

Под действием случайных помех фаза опорного генератора может скачком изменяться на 180°, тогда опорное напряжение будет по фазе совпадать не с сигналом 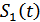, а с сигналом 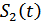. А т.к. при ДФМ 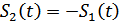, то неправильная фаза опорного генератора приводит к появлению «обратной работы», когда сигналы 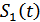принимаются как 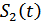и наоборот (для двоичного сигнала это означает, что сигналы «1» превращаются в «0», а «0» в «1» ).

Для устранения опасности «обратной работы» применяется «относительная» фазовая модуляция (ДОФМ). Если при обычной дискретной фазовой модуляции прием осуществляется путем сравнения фаз приходящего сигнала с фазой опорного генератора, то при ДОФМ осуществляется сравнение фазы каждой посылки с фазой предыдущей посылки. Если фаза очередной посылки совпадает с фазой предыдущей посылки, то приемник выдает «1», если же фазы противоположны, приемник выдает «0». Возможен когерентный и некогерентный прием ДОФМ. При когерентном приеме в приемнике используется опорный генератор, а снятие (устранение) относительности осуществляется путем детектирования сигналов (рис. 9.28). Для этой цели сигнал с выхода синхронного детектора подается на ячейку памяти ЯП и схему сравнения полярностей ССП. На другой вход системы ССП подается сигнал с ячейки памяти, задержанный на время, равное длительности элементарной посылки принимаемых сигналов.

Рисунок 9.28. Структурная схема приемника ДОФМ (ССП)

Таким образом, схема сравнения полярностей сравнивает полярности принимаемой посылки и предыдущей посылки. При совпадении полярностей схема выдает «1», при несовпадении – «0».

Особенностью ДОФМ является сдваивание ошибок, возникающих из-за помех, т.к. любая искаженная посылка поступает на схему сравнения полярностей дважды: сначала непосредственно, а затем – через ячейку памяти. При малой вероятности ошибок эта вероятность вдвое больше, чем вероятность ошибки при приеме сигналов дискретной фазовой модуляции.

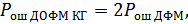
или

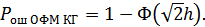
Схема приемника ДОФМ для некогерентного приема приведена на рис. 9.29. В этой схеме вместо опорного генератора используется линия задержки, задерживающая входной высокочастотный сигнал на время, равное длительности элементарной посылки. В отличие от предыдущей схемы, опорное напряжение в данной схеме содержит кроме высокочастотного напряжения предыдущей посылки также составляющую помехи, в результате чего эта схема обеспечивает меньшую помехоустойчивость, чем схема когерентного приема.

Рисунок 9.29. Структурная схема приемника ДОФМ (ССФ)

Вероятность ошибки при этом определяется формулой:

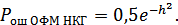
Иногда для некогерентного приема ДОФМ применяют квадратурную схему приема (для сигналов ДЧМ такая схема приведена на рис. 9.21).

Максимальная помехоустойчивость приемника (рис. 9.29) при флуктуа­ци­он­ных помехах имеет место в том случае, когда в качестве фильтров ФНЧ используются оптимальные фильтры. При этом обеспечивается .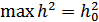

9.15. Помехоустойчивость передачи непрерывных сообщений

Пусть наблюдается колебание

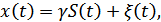
где – точно известный сигнал,

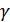– амплитудный множитель, подлежащий оцениванию,

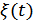– гауссовский шум с нулевым средним и спектральной плотностью 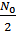, постоянной в полосе 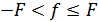(квазибелый шум). Найдем правило оценивания параметра 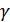, оптимальное по критерию максимального правдоподобия.

Возьмем отсчетов наблюдаемого колебания на интервале наблюдения 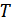с шагом 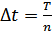, при этом отсчеты шума являются некоррелированными. Совместная плотность распределения вероятности взятых отсчетов равна:

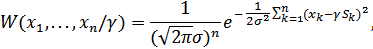
где 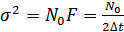. Устремляя 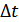к нулю ( 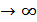), запишем функцию правдоподобия:

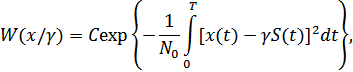
где 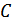– константа, не существенная для задачи оценивания.

Для нахождения правила оценивания следует продифференцировать функцию правдоподобия или ее логарифм и приравнять к нулю. Полученное при этом уравнение правдоподобия:

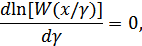
для данного случая имеет вид:

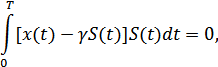
откуда:

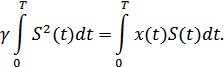
Решением этого уравнения относительно 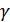является 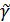, определяемая выражением:

где 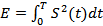– энергия сигнала, известная по условия задачи.

Качество полученной МП-оценки можно оценить, подставив в (9.57) выражение :

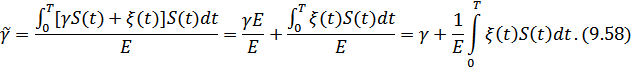
Второе слагаемое представляет собой ошибку оценивания. Таким образом, оценка тем точнее, чем больше энергия сигнала (для гармонического сигнала увеличение энергии эквивалентно увеличению длительности интервала наблюдения) и чем меньше спектральная плотность мощности помехи.

Из выражения (9.58) видно, что оценка несмещенная, т.к. 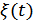имеет нулевое математическое ожидание.

Полученный алгоритм оценивания может быть реализован в виде структурной схемы.

Рисунок 9.30. а) структурная схема оценивания амплитуды сигнала

б) синхронный детектор АМ-колебаний

Полученное правило оценивания амплитуды сигнала можно использовать и при медленном изменении этого параметра; вместо интеграла можно применить ФНЧ, и при гармоническом сигнале схема рис. 9.30, а) превращается в схему синхронного детектора амплитудно-модулированных колебаний (рис. 9.30, б).

10. Основы теории информации

10.1. Информационные характеристики сигнала

Системы связи служит для передачи сообщений от производителя к получателю. Однако не всякое сообщение содержит информацию.

Информация – это совокупность сведений об объекте или явлении, которые увеличивают знания потребителя об этом объекте или явлении.

В математической теории связи (теории информации) исходят из того, что в некотором сообщении 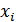количество информации 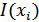зависит не от ее конкретного содержания, степени важности и т.д., а от того, каким образом выбирается данное сообщение из общей совокупности возможных сообщений.