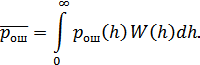В ряде случаев согласованные фильтры оказываются практически трудно реализуемыми. Поэтому часто применяются фильтры, которые согласованы с сигналом только по полосе – квазиоптимальные фильтры.
Квазиоптимальный фильтр обеспечивает при заданной форме амплитудно-частотной характеристики максимальное отношение сигнал/шум. Квазиоптимальный фильтр согласован с сигналом не по форме, а лишь по ширине полосы пропускания.
Можно показать, что для прямоугольного радиоимпульса максимальное отношение сигнал/шум обеспечивается при ширине полосы, равной:
a) 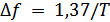 – при использовании идеального полосового фильтра с прямоугольной АЧХ;
– при использовании идеального полосового фильтра с прямоугольной АЧХ;
b) 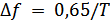 – при использовании одиночного колебательного контура;
– при использовании одиночного колебательного контура;
c) 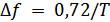 – при использовании фильтра с характеристикой вида гауссовой прямой.
– при использовании фильтра с характеристикой вида гауссовой прямой.
Для перечисленных квазиоптимальных фильтров отношение сигнал/шум (по мощности) уменьшается по сравнению с согласованным фильтром соответственно на 18%, 19% и 9%. Если квазиоптимальный фильтр дополнить схемой гашения колебаний в конце посылки, то такой фильтр по своим свойствам будет приближаться к согласованному.
Приведенные выше значения оптимальной полосы и энергитического проигрыша справедливы для приема одиночного импульса.
При передаче сообщений на фильтр воздействует последовательность импульсов илм шумов. В этом случае при узкой полосе пропускания после окончания элемента сигнала в фильтре существуют остаточные колебания, которые действуют как дополнительная помеха при приеме следующих элементов сигнала. Переходные процессы требуют увеличения полосы пропускания примерно до величины 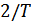 (для фильтра с прямоугольной характеристикой), что приводит к энергетическому проигрышу по сравнению с оптимальным фильтром примерно в два раза. Кроме того, в реальных условиях частота сигшнала и АЧХ фильтра не стабильны, что требует дополнительного расширения полосы пропускания фильтра и приводит к дальнейшему уменьшению отношения сигнал/шум.
(для фильтра с прямоугольной характеристикой), что приводит к энергетическому проигрышу по сравнению с оптимальным фильтром примерно в два раза. Кроме того, в реальных условиях частота сигшнала и АЧХ фильтра не стабильны, что требует дополнительного расширения полосы пропускания фильтра и приводит к дальнейшему уменьшению отношения сигнал/шум.
9.8. Оптимальная фильтрация непрерывных сообщений
При передаче непрерывных сообщений решается задача воспроизведения формы. Задача оптимальной фильтрации: необходимо так обработать поступающую на вход смесь сигнала и помехи 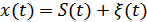 , чтобы получить на выходе применика сообщение
, чтобы получить на выходе применика сообщение 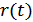 , наименее отличающееся от переданного
, наименее отличающееся от переданного 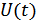 с точки зрения критерия качества.
с точки зрения критерия качества.
При рассмотрении критерия качества передачи непрерывных сообщений было установлено, что мерой качества переданного сообщения может быть среднеквадратическое отклонение:

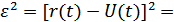
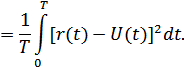
Следовательно, критерием оптимального приема непрерывных сообщений можно считать минимум 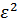 .
.
Передача непрерывных сообщений может производиться как немодулированными, так и модулированными сигналами. При использовании немодулированных сигналов, отображающих это сообщение или сигнал, связанных линейной зависимостью 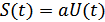 , можно считать, что получение сообщения на выходе приемника является оптимальным. Однако чаще передача сообщений производится модулированными сигналами, при этом информация о переданном сообщении заложена в изменении одного или нескольких параметров некоторого сигнала-переносчитка, т.е.:
, можно считать, что получение сообщения на выходе приемника является оптимальным. Однако чаще передача сообщений производится модулированными сигналами, при этом информация о переданном сообщении заложена в изменении одного или нескольких параметров некоторого сигнала-переносчитка, т.е.:
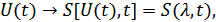
где 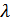 – модулируемый параметр сигнала.
– модулируемый параметр сигнала.
Применительно к двум способам передачи сообщений различают две задачи:
1. Требуется воспроизвести с 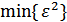 сигнал
сигнал  :
:

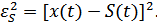
2. Требуется воспроизвести с 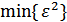 сообщение
сообщение 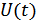 , переносимое сигналом
, переносимое сигналом 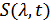 .
.

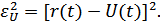
При использовании немодулированных сигналов:
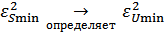
При модулированных сигналах это условие не выполняется.
Рисунок 9.18. Структурная схема приема непрерывных сообщений
Операции усиления не являются принципиальными, изменяется лишь масштаб. Помехоустойчивость приема сообщений определяется в основном флуктуациями сигналов (ФВЧ) и детектированием.
Особенность и сложность фильтрации непрерывных сообщений в том, что конкретная форма реализации на приеме неизвестна, а заданы лишь энергетические спектры сигнала и помехи и вид модуляции.
9.9. Оптимальная фильтрация непрерывных сигналов
Практически эта задача была решена Котельниковым и Винером в предположении, что сигналы и помехи – стационарные процессы.
По той же теории линейной оптимальной фильтрации коэффициент передачи фильтра 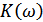 , минимизирующий
, минимизирующий 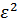 , определяется:
, определяется:
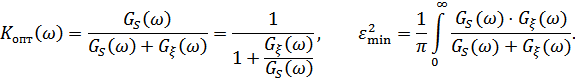
1. Ошибка может быть 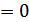 при условии, что
при условии, что 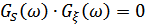 , т.е. спектры сигнала и помехи не перекрываются, при этом
, т.е. спектры сигнала и помехи не перекрываются, при этом 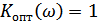 в пределах
в пределах 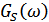 , т.е. АЧХ – прямоугольная.
, т.е. АЧХ – прямоугольная.
Рисунок 9.19. Сигнал по спектру чист от помех. Помеха полностью отфильтровывается
При перекрытии спектра 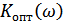 должен быть таким, что различные частотные состаявляющие сигнала пропускаются с тем большим ослаблением, чем меньше отношение
должен быть таким, что различные частотные состаявляющие сигнала пропускаются с тем большим ослаблением, чем меньше отношение 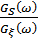 .
.
При малых отношениях с/ш восстановление сигнала практически невозможно ( 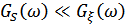 ).
).
С учетом изложенного: при передаче сообщения, модулированного сигналами, фильтр, обеспечивающий 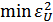 , ставится в приемнике после демодулятора. А до демодулятора используются фильтры, обеспечивающие
, ставится в приемнике после демодулятора. А до демодулятора используются фильтры, обеспечивающие 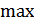 отношение сигнал/помеха.
отношение сигнал/помеха.
Линейный фильтр – оптимальный только для сигнала 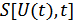 , а не для самого сообщения
, а не для самого сообщения 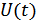 . Передаваемый сигнал
. Передаваемый сигнал  нелинейно связан с
нелинейно связан с 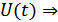 оптимальная фильтрация непрерывных сообщений является задачей нелинейной фильтрации.
оптимальная фильтрация непрерывных сообщений является задачей нелинейной фильтрации.
Устройство нелинейной фильтрации изменяет свои параметры, используя результаты обработки принятого сигнала за некоторый промежуток времени 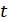 , т.е. является следящим за изменениями модулируемого параметра сигнала.
, т.е. является следящим за изменениями модулируемого параметра сигнала.
9.10. Отношение с/ш на входе приемника непрерывных сообщений
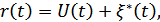
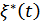 – эквивалентная (эффективная) помеха на выходе приемника.
– эквивалентная (эффективная) помеха на выходе приемника.
Влияние помех на передаваемый сигнал будет проявляться в виде дополнительного изменения модулируемого параметра, т.е. в виде паразитной модуляции.


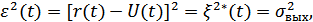
т.е. ошибка на выходе приемника – мощность помехи на выходе приемника.
Пусть на вход действует сигнал  и аддитивная помеха
и аддитивная помеха 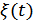 .
.
 имеет мощность
имеет мощность 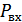 .
.
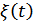 имеет спектральную плотность
имеет спектральную плотность 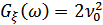 .
.
Определим с/ш на входе:
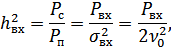
где 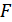 – полоса пропускания приемника, определяемая шириной спектра сигнала,
– полоса пропускания приемника, определяемая шириной спектра сигнала,
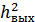 – с/ш на выходе приемника. Зависит не только от
– с/ш на выходе приемника. Зависит не только от 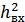 , но и от вида модуляции и способа приема.
, но и от вида модуляции и способа приема.
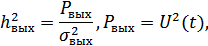
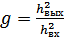 – энергетический выигрыш.
– энергетический выигрыш. 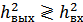 .
.
Есть способы модуляции приема, при которых 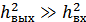 (применяются).
(применяются).
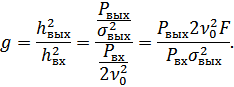
Энергетический выигрыш 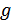 может использоваться в качестве меры помехоустойчивого приемника. Однако эта мера не всегда объективна, т.к. зависит от ширины ПП, а следовательно и от вида модуляции. Для объективной сравнительной оценки различных способов модуляции вводят обобщенный энергетический выигрыш
может использоваться в качестве меры помехоустойчивого приемника. Однако эта мера не всегда объективна, т.к. зависит от ширины ПП, а следовательно и от вида модуляции. Для объективной сравнительной оценки различных способов модуляции вводят обобщенный энергетический выигрыш 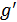 , позволяющий сравнивать не при одинаковых
, позволяющий сравнивать не при одинаковых 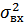 , а при одинаковой величине спектральной плотности помехи
, а при одинаковой величине спектральной плотности помехи 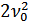 .
.
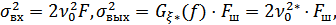
где 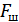 – ширина спектра сообщения,
– ширина спектра сообщения,
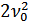 – спектральная плотность эквивалентной помехи на выходе приемника.
– спектральная плотность эквивалентной помехи на выходе приемника.
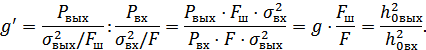
Выясним физический смысл 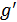 .
.
Пусть на входе – сигнал длительностью 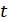 . Умножим числитель и знаменатель
. Умножим числитель и знаменатель 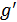 на
на 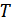 :
:
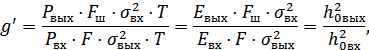
где 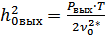 – отношение энергии сигнала на выходе к спектральной плотности помехи,
– отношение энергии сигнала на выходе к спектральной плотности помехи,
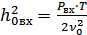 – отношение энергии сигнала на выходе к спектральной плотности помехи.
– отношение энергии сигнала на выходе к спектральной плотности помехи.
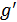 показывает, во сколько раз возрастает отношение энергии сигнала/помехи на выходе по сравнению со входом.
показывает, во сколько раз возрастает отношение энергии сигнала/помехи на выходе по сравнению со входом.
Задача определения помехоустойчивого приема непрерывных сигналов сводится к определению 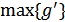 .
.
9.11. Обеляющий фильтр
При построении оптимальных решающих устройств (оптимального приемника Котельникова и согласованного фильтра) предполагалось, что аддитивной помехой является нормальный белый шум. Рассмотрим, что изменяется, если шум будет по прежнему нормальным, но не белым.
Задачу выбора оптимальной решающей схемы и вычисления вероятности правильного приема символа при нормальном шуме с неравномерным спектром можно свести к аналогичной задаче при белом шуме следующего метода, впервые предложенного В.А. Котельниковым.
Для случая не белого шума определили схемы оптимального приемника. Пусть теперь на вход приемного устройства поступает сигнал  и нормальный шум
и нормальный шум 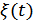 с энергетической спектральной плотностью
с энергетической спектральной плотностью 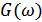 . Если пропустить эту смесь сигнала и шума через линейный фильтр
. Если пропустить эту смесь сигнала и шума через линейный фильтр 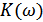 , частотная характеристика которого
, частотная характеристика которого 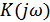 с точностью до постоянного коэффициента удовлетворяет условию
с точностью до постоянного коэффициента удовлетворяет условию
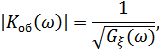
то на выходе фильтра шум становится не только нормальным (т.к. фильтр линейный), но и окажется белым, т.к. его энергетический спектр будет:
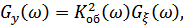
но 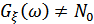 , следовательно
, следовательно 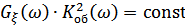 (белый шум), но
(белый шум), но 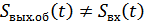 , значит на передаче нужно ввести предискажения:
, значит на передаче нужно ввести предискажения:
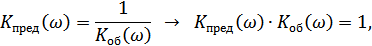
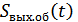 – сигнал на выходе обеляющего фильтра,
– сигнал на выходе обеляющего фильтра,
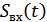 – сигнал на входе обеляющего фильтра.
– сигнал на входе обеляющего фильтра.
Рисунок 9.20. Примеры использования обеляющего фильтра на передаче при:
а) использовании СФ
б) использовании коррелятора
9.12. Прием сигналов с неизвестной фазой (некогерентный прием)
В приемнике Котеликова местные генераторы опорных сигналов 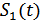 и
и 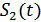 должны генерировать сигналы с точностью до фазы принимаемых сигналов. Для этого фаза принимаемого
должны генерировать сигналы с точностью до фазы принимаемых сигналов. Для этого фаза принимаемого 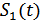 и
и 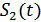 измеряется и используется для синхронизации опорных генераторов. Такой приемник называется приемником с известной фазой (когерентным приемником), в отличие от приемника с неизвестной фазой (некогерентного приемника).
измеряется и используется для синхронизации опорных генераторов. Такой приемник называется приемником с известной фазой (когерентным приемником), в отличие от приемника с неизвестной фазой (некогерентного приемника).
Прием сигнала с неизвестной фазой используется в следующих случаях:
1. Формирование сигналов 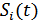 в передатчике производится без учета фазы несущего колебания, в результате чего фаза несущего колебания в каждом сигнале
в передатчике производится без учета фазы несущего колебания, в результате чего фаза несущего колебания в каждом сигнале 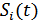 является случайной.
является случайной.
2. В канале связи наблюдаются случайные скачки фазы с большой дисперсией.
3. Реализация когерентного приема экономически нецелесообразна из-за необходимости использования синхронизируемых опорных генераторов сигналов 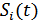 .
.
Посмотрим, что произойдет при наличии случайного сдвига фаз. Пусть сигнал 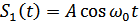 , а опорный сигнал приемника
, а опорный сигнал приемника 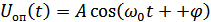 . После перемножения и интегрирования этих сигналов получим:
. После перемножения и интегрирования этих сигналов получим:
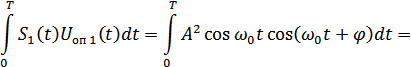
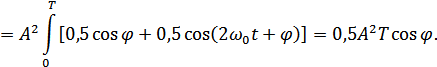
Отсюда видно, что при наличие сдвига 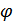 функция взаимной корреляции умножается на
функция взаимной корреляции умножается на 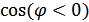 . Только при
. Только при 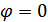
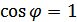 и приемник будет оптимальным и когерентным. При наличие свига фаз помехоустойчивость приемника уменьшается.
и приемник будет оптимальным и когерентным. При наличие свига фаз помехоустойчивость приемника уменьшается.
Рассмотрим в качестве примера оптимальный некогерентный приемник двух сигналов ДЧМ. На приемнике разделение сигналов двух частот осуществляется с помощью квадратурной схемы приема и двух ветвей обработки сигналов 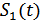 и
и 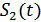 . Для этого каждая ветвь иметь два перемножителя, генератор опорного напряжения частоты, фазовращатель на 90°. Далее с помощью интеграторов, квадраторов и сумматоров определяется значение амплитуды сигнала.
. Для этого каждая ветвь иметь два перемножителя, генератор опорного напряжения частоты, фазовращатель на 90°. Далее с помощью интеграторов, квадраторов и сумматоров определяется значение амплитуды сигнала.
С выводов аналоговых сумматоров сигналы подаются на схему сравнения, которая реализует правило решения: если 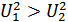 , то сигнал
, то сигнал  , иначе
, иначе 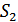 .
.
Если интеграторы в схеме (рис. 9.19) являются оптимальными, то для сигналов с неизвестной фазой (и одинаковой энергией) реализуется оптимальное правило решения вида:
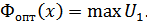
Приведенная схема нечувствительна (инвариантна) по отношению к фазам приходящих сигналов (или фазам опорных генераторов Г1 и Г2). Чтобы в этом убедиться, рассмотрим работу верхней половины схемы, когда на ее вход поступает сигнал 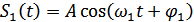 , где
, где 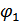 – случайная (неизвестная) фаза сигнала. Помехи на входе приемника учитывать не будем.
– случайная (неизвестная) фаза сигнала. Помехи на входе приемника учитывать не будем.
Квадратурная схема
Рисунок 9.21. Квадратурная структурная схема НКГ приемника ДЧМ
Найдем величину 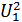 на выходе первого сумматора, если два опорных напряжения излучаются по закону
на выходе первого сумматора, если два опорных напряжения излучаются по закону 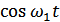 и
и 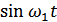 (сдвинуты на 90°, т.е. находятся в квадратуре). Вычислим сначала напряжение на выходе первого и второго интеграторов:
(сдвинуты на 90°, т.е. находятся в квадратуре). Вычислим сначала напряжение на выходе первого и второго интеграторов:
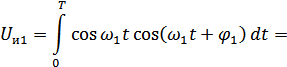
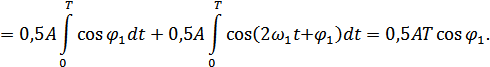
Аналогично получим:
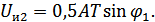
Отсюда:
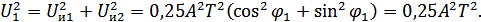
Таким образом, на выходе первого сумматора получим сумму квадратов напряжений, пропорциональную энергии сигнала  . От фазы сигнала эта величина не зависит. В этом и заключается преимущество подобного способа приема.
. От фазы сигнала эта величина не зависит. В этом и заключается преимущество подобного способа приема.
Следует заметить, что на первом входе решающей схемы при поступлении на вход приемника сигнала 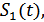 кроме найденной величины
кроме найденной величины 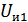 , будет поступать так же помеха
, будет поступать так же помеха 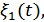 прошедшая вместе с сигналом весь тракт обработки сигнала
прошедшая вместе с сигналом весь тракт обработки сигнала  . На втором входе решающего устройства будет существовать помеха
. На втором входе решающего устройства будет существовать помеха 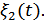
При наличии помехи на входе приемника при обработке сигналов с помехой происходит сложное их взаимодействие. Мы не будем рассматривать этот вопрос. Заметим только, что в процессе анализа помеха 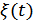 разлагается на квадратурные составляющие, синфазные с опорными напряжениями
разлагается на квадратурные составляющие, синфазные с опорными напряжениями 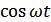 и
и 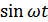 .
.
Оптимальное правило решения для двух сигналов ДЧМ может быть реализованно и с помощью схемы рис. 9.22.
Рисунок 9.22. Структурная схема оптимального НКГ приемника ДЧМ
На входе приемника сигнал  представляет собой сумму
представляет собой сумму 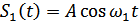 или
или 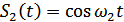 и помеху
и помеху 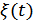 . В схеме приемника имеются оптимальные фильтры СФ1 и СФ2, согласованные с сигналами
. В схеме приемника имеются оптимальные фильтры СФ1 и СФ2, согласованные с сигналами 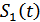 и
и 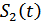 . Далее идут амплитудные детекторы Д1 и Д2, схема вычитания, ФНЧ и РУ, которое, в зависимости от полярности сигнала на его входе, выдает
. Далее идут амплитудные детекторы Д1 и Д2, схема вычитания, ФНЧ и РУ, которое, в зависимости от полярности сигнала на его входе, выдает  или
или 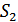 .
.
Пусть на вход приемника поступает сигнал. Тогда на выходе первого фильтра мы будем иметь сумму сигнала 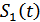 и помехи
и помехи 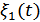 , а на выходе второго фильтра только помеху
, а на выходе второго фильтра только помеху 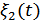 .
.
Реализации помех 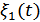 и
и  – различные, т.к. каждая помеха прошла через свой полосовой фильтр. После детектирования сигналов на выходе детектора Д1 мы будем иметь огибающую суммы сигнала и помехи, распределенную по закону Райса:
– различные, т.к. каждая помеха прошла через свой полосовой фильтр. После детектирования сигналов на выходе детектора Д1 мы будем иметь огибающую суммы сигнала и помехи, распределенную по закону Райса:
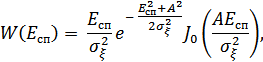
а на выходе Д2 получим огибающую помехи, распределенную по закону Рэлея:
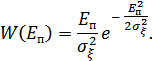
При малой помехе напряжение на выходе первого детектора  будет больше, чем напряжение на выходе второго детектора
будет больше, чем напряжение на выходе второго детектора 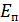 , разность
, разность 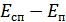 будет положительной, и решающее устройство выдает
будет положительной, и решающее устройство выдает  . Однако, при сильной помехе может случиться, что
. Однако, при сильной помехе может случиться, что 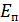 превысит
превысит 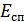 , и схема ошибочно выдаст сигнал
, и схема ошибочно выдаст сигнал 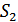 . Сказанное поясняется рис. 9.23, на котором приведены зависимости
. Сказанное поясняется рис. 9.23, на котором приведены зависимости 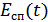 и
и 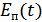 .
.
Рисунок 9.23. Пример превышения помехой уровня сигнала
Как видно из рисунка, на интервале времени 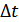
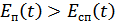 ; вероятность этого события и есть вероятность ошибки на выходе данного приемника.
; вероятность этого события и есть вероятность ошибки на выходе данного приемника.
Рисунок 9.24. ФПВ помехи и суммы сигнал + помеха
На рис. 9.24 приведены графики плотностей вероятности простого и обобщенного законов Рэлея. Допустим, в какой-то момент времени величина 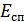 на выходе первого детектора известна. Тогда можно определить вероятность ошибки как вероятность того, что огибающая помехи
на выходе первого детектора известна. Тогда можно определить вероятность ошибки как вероятность того, что огибающая помехи 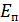 превысит данное значение
превысит данное значение 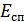 (заштрихованная часть на рис. 9.24).
(заштрихованная часть на рис. 9.24).
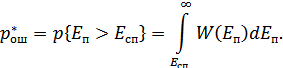
Подставим сюда 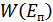 , произведем интегрирование и получим:
, произведем интегрирование и получим:
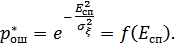
В результате мы получили зависимость вероятности ошибки как функцию 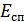 . Величина
. Величина 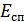 из рис. 9.24 известна. Однако в действительности эта величина случайная, определяемая распределением Райса. Поэтому величину
из рис. 9.24 известна. Однако в действительности эта величина случайная, определяемая распределением Райса. Поэтому величину 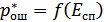 надо усреднить по всем возможным изменениям
надо усреднить по всем возможным изменениям 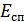 от
от 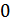 до
до 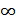 . Тогда:
. Тогда:
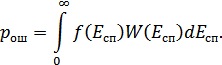
Если сюда подставить формулу распределения Райса и 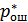 , то после интегрирования получим:
, то после интегрирования получим:
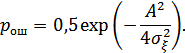
Но 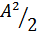 есть мощность сигнала
есть мощность сигнала 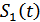 .
.
Введем обозначения:
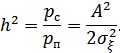
Тогда окончательно получим:
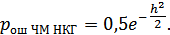
Помехоустойчивость некогерентного приема ниже, чем помехоустойчи-вость оптимального приемника Котельникова.
Если фильтры на входе приемника являются оптимальными, то
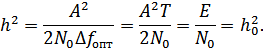
Можно показать, что при дискретной амплитудной модуляции вероятность ошибки при некогерентном приеме определяется формулой:
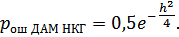
Отсюда видно, что при переходе от ДАМ к ДЧМ имеется энергетический проигрыш (по максимальной мощности), равный двум.
При сравнении помехоустойчивости когерентного и некогерентного приемов можно убедиться, что при когерентном приеме вероятность ошибки значительно меньше, чем при некогерентном. Это объясняется тем, что при некогерентном приеме флуктуационная помеха полностью влияет на помехоустойчивость приема. При когерентном приеме на вероятность ошибки влияет только синфазная составляющая помехи, квадратурная же составляющая подавляется синхронным детектором, в результате чего когерентный прием обеспечивает практически двукратный энергетический выигрыш по сравнению с некогерентным приемом, т.к. мощность огибающей помехи в два раза выше мощности ее квадратурных составляющих.
Рисунок 9.25. Кривые помехоустойчивости различных видов модуляции и способов приема
9.13. Прием дискретных сигналов со случайной амплитудой
В некоторых системах связи амплитуда принимаемого сигнала является случайной из-за мультипликативных помех. В этом случае для нахождения вероятностей ошибки, в зависимости от способа приема сигналов, вначале определяют по известным формулам вероятностей ошибки как для канала с постоянными параметрами. Например, для ЧМ КГ:
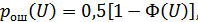
а для ЧМ НКГ:
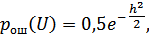
и т.д.
Затем определяется плотность вероятностей, учитывающих случайные изменения амплитуды сигнала. Наконец, находится среднее значение 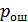 как математическое ожидание
как математическое ожидание 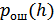 по формуле:
по формуле: