Отношение сигнал/помеха определяется, как обычно, формулой
где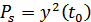 
– мощность сигнала на выходе фильтра в момент 
,
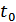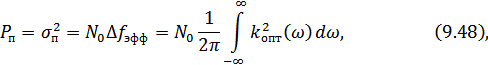
где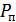 
– мощность (дисперсия) помехи на выходе фильтра,
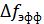– эффективная полоса пропускания оптимального фильтра.
Подставляя в (9.47) выражение (9.37) и (9.48) с учетом (9.38), получим
где
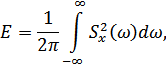
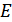– энергия сигнала 
на выходе фильтра.
Из (9.49) видно, что отношение сигнал/помеха численно равно отношению сигнала к спектральной плотности помехи (как в приемнике Котельникова) и не зависит от формы сигнала. А т.к. энергия сигнала равна произведению мощности сигнала на его длительность, то для повышения помехоустойчивости систем связи с использованием согласованных фильтров (СФ) можно увеличивать длительность элементарных сигналов, что и делается в широкополосных системах связи.
При применении в демодуляторе приемника согласованных фильтров в сочетании с когерентным способом приема можно достичь потенциальной помехоустойчивости.
Импульсная характеристика оптимального фильтра (отклик фильтра на дельта-функцию) определяется известным выражением
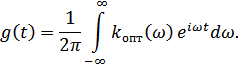
Подставив сюда значение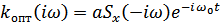 
из (9.46), получим:
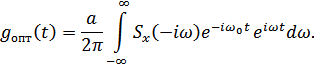
Интегрирование в последней формуле производится по всем частотам от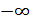 
до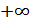 
, поэтому знак перед 
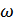в этой формуле можно изменить на противоположный, что не приведет к изменению результата вычисления интеграла. В результате получим:
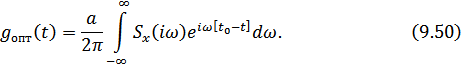
А т.к. на основании преобразования Фурье
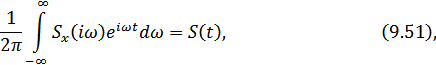
то, сравнивая (9.42) и (9.43), получаем
Таким образом, функция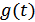 
отличается от только постоянным множителем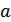 
, смещением на величину 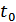и знаком аргумента 
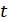(т.е. функция 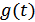является зеркальным отображением , сдвинутым на величину )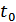
На рис. 9.12 в качестве примера приведен некоторый сигнал , зеркально перевернутый сигнал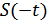 
и функция 
.
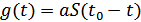Рисунок 9.12. Пример получения 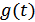СФ
Как уже говорилось, величину 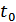обычно берут равной длительности сигнала 
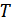. При поступлении на вход системы сигнала 
определяется известным интегралом Дюамеля
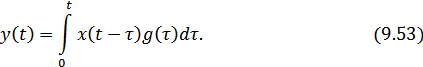
Пусть на вход оптимального фильтра поступает аддитивная смесь, содержащая сигнал , с которым фильтр согласован, и помеха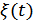 
(это может быть флуктуационная помеха или какой-нибудь детерминированный сигнал, с которым фильтр не согласован): 
.
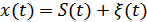Подставляя и учитывая (9.44), получаем:
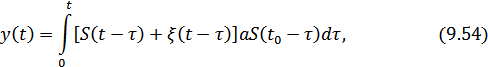
заменяя 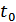на 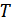, получим:
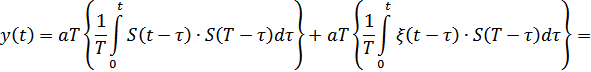
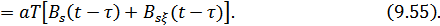
Таким образом, на выходе согласованного фильтра получаем под действием сигнала функцию корреляции сигнала, а под действием помехи – функцию взаимной корреляции сигнла и помехи. Если на входе фильтра только помеха (без сигнала), на выходе получаем только функцию взаимной корреляции помехи и сигнала, с которой фильтр согласован.
В формуле (9.55) 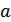– любой произвольный множитель, поэтому произведение 
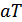можно заменить на произвольный множитель 
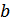. В момент времени 
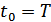(момент отсчета) формула (9.55) дает
Примечание: если на вход согласованного фильтра поступает флуктуационная помеха, то теоретически функция взаимной корреляции должна быть равна нулю, т.к. сигнал и помеха являются независимыми функциями времени. Однако на практике это не так, т.к. при вычислении функции корреляции требуется бесконечно большое время интегрирования. В нашем же случае интегрирование ведется за время, равное 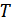, поэтому значение является приближенным. Результаты фильтрации не зависят от формы сигнала, следовательно, фильтр может быть применен и без детектора. Тогда оптимальный приемник полностью известных сигналов может быть реализован в виде двух согласованных фильтров СФ1 и СФ2 и устройства сопротивления.
Рисунок 9.13. Оптимальный приемник на СФ
9.7. Примеры согласованных фильтров. Квазиоптимальные фильтры
Рассмотрим согласованный фильтр для прямоугольного фильтра для прямоугольного импульса длительности 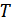. Спектральная плотность такого импульса равна
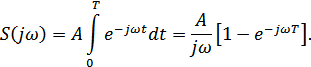
Для согласованного фильтра в случае :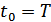
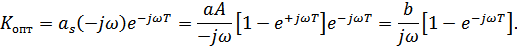
Пользуясь последним выражением, можно легко построить схему фильтра для данного случая. Т.к. из теории электрических цепей известно, что деление на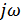 
означает интегрирование сигнала, а множитель 
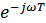означает задержку сигнала на время 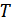, в результате схема фильтра будет содержать интегратор, линию задержки и вычитатель.
Рисунок 9.14. Пример реализации СФ
Таким образом, на выходе фильтра получится треугольный импульс с основанием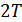 
(это – функция корреляции входного импульса прямоуголной формы). То, что выходной импульс имеет в два раза большую длительность, чем входной, является недостатком оптимального фильтра, т.к. «хвост» выходного сигнала на отрезке времени от 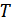до 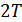будет накладываться на входной сигнал следующего импульса. Поэтому на практике часто применяют упрощенную схему фильтра, содержащую интегрирующую 
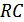-цепь ( 
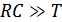) и ключ 
.
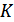Рисунок 9.15. Вид сигналов в различных точках СФ
В момент 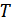окончания входного импульса ключ 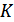замыкается, конденсатор интегратора быстро разряжается через ключ, и схема готова к приему следующего импульса.
Рисунок 9.16. Пример кинематического фильтра для видеоимпульса
Оптимальный фильтр для приема радиоимпульсов с прямоугольной огибающей может быть построен аналогичным образом, однако 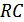-цепочка должна быть заменена колебательным контуром с достаточно высокой добротностью. Фильтры с ключами называются «кинематическими» фильтрами.
Рисунок 9.17. Пример кинематического фильтра для радиоимпульса