1. Дискретная амплитудная модуляция (ДАМ).
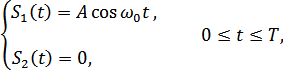
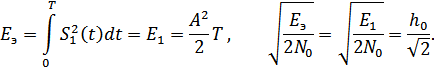
Подставляя это значение в (9.24), получим:
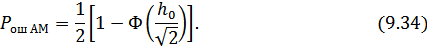
2. Дискретная частотная модуляция (ДЧМ).
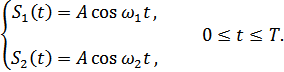
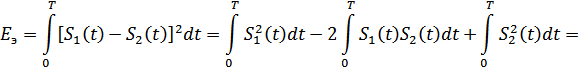
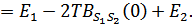
При частотной дискретной модуляции сигналы являются взаимоортогональными, поэтому их функция взаимной корреляции равна нулю. Кроме того, благодаря равной амплитуде сигналов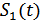 
и 
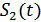
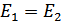. В результате 
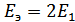, а
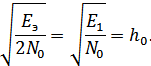
Подставляя эту величину в (9.24), получим:
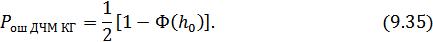
3. Дискретная фазовая модуляция (ДФМ).
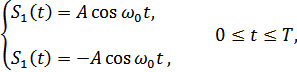
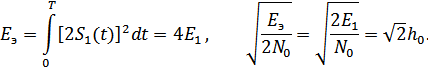
Подставляя эту величину в (9.24), получим:
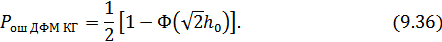
Сравнивая между собой формулы (9.34), (9.35), (9.36), видим, что для достижения заданной вероятности ошибки при ДЧМ требуется величина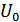 
в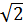 
раз больше, чем при ДФМ, а при ДАМ в 2 раза больше, чем при ДФМ. Отсюда видно, что переход от ДАМ к ДЧМ дает двухкратный выигрыш по мощности, а к ДФМ – четырехкратный выигрыш. Причину этого можно наглядно установить, рассматривая векторные диаграммы сигналов для разных видов модуляции.
Рисунок 9.9. Векторные диаграммы сигналов дискретной модуляции
Из рисунка видно, что при ДАМ расстояние между векторами сигналов 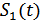и 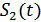равно длине вектора 
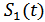, при ДЧМ (взаимоортогональные сигналы) это расстояние равно 
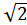, а при ДФМ (противооложные сигналы) это расстояние равно 
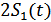. Энергия же пропорциональна квадрату разности сигналов.
Следует заметить, что приведенные здесь данные об энергетике сигналов ДАМ, ДЧМ и ДФМ относились к максимальным (пиковым) мощностям этих сигналов. В этом смысле, например, при переходе от ДЧМ к ДАМ мы имеем двухкратный выигрыш в пиковой мощности.
Однако, сигналы ДАМ имеют пассивную паузу (мощность сигнала в паузе равна нулю), поэтому по потребляемой передатчиком мощности, кроме отмеченного ранее проигрыша, имеется еще и двухкратный выигрыш. С учетом этого обстоятельства при переходе от ДЧМ к ДАМ двухкратный проигрыш по пиковой мощности компенсируется двухкратным выигрышем за счет пассивной паузы сигналов ДАМ., в результате чего по потребляемой мощности эти сигналы оказываются равноценными. Однако, следует помнить, что при ДАМ в приемнике Котельникова трудно установить необходимый порог в сравнивающем (решающем) устройстве, а в приемнике ДЧМ регулировка порога не требуется. Поэтому частотная модуляция применяется чаще, чем амплитудная.
Отметим еще раз, что приемник Котельникова обеспечивает наилучшую (потенциальную) помехоустойчивость. Это достигается благодаря тому, что при приеме учитываются все параметры сигнала, не несущие информации: амплитуда, частота, фаза несущего колебания, а также длительность сигнала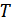 
, т.к. интегрирование (фильтрация) осуществляется в течении этого времени. Решение о принятом сигнале обычно осуществляется в конце каждого интервала 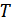, для чего в приемнике должна иметься специальная система синхронизации элементов сигнала.
Рисунок 9.10. Кривые помехоустойчивости дискретной модуляции
9.6. Оптимальная фильтрация дискретных сигналов
Оптимальный приемник является корреляционным; сигнал на его выходе представляет собой функцию корреляции принимаемого сигнала 
и ожидаемого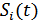 
, благодаря чему обеспечивается максимально возможное отношение сигнал/шум 
.
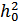Рисунок 9.11. Сущность оптимальной фильтрации
Поскольку опрерация определения функции корреляции является линейной, ее можно реализовать в некотором линейном фильтре, характеристики которого (комплексная передаточная характеристика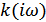 
и импульсная характкристика 
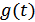) являются такими, что отношение сигнал/шум на его выходе получается максимальным, причем
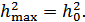
Найдем характеристики фильтра, когда помеха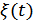 
является флуктуационной со спектральной плотностю 
, 
.
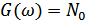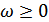Пусть сигнал на входе фильтра имеет комплексный спектр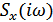 
. Тогда сигнал на выходе фильтра 
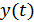можно определить с помощью преобразования Фурье
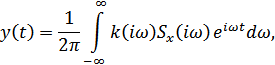
где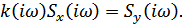 
Нас интересует значение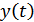 
в момент принятия решения (момент отссчета 
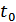), поэтому, заменив 
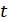на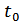 
, получим:
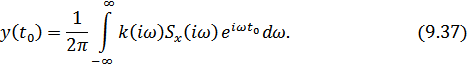
Чтобы получить максимальную величину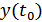 
, нужно найти оптимальную характеристику фильтра 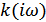. Для этой цели можно воспользоваться известным неравенством Шварца-Буняковского, имеющим вид:
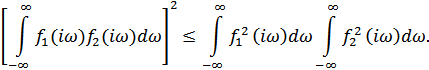
Легко проверить, что данное неравенство превращается в равенство при условии, что
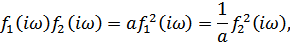
где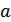 
– любая произвольная постоянная. В нашем случае, применительно к формуле (9.29), величина будем максимальной при условии
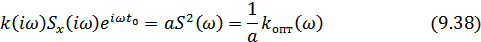
(это условие оптимальности характеристики 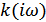, поэтому здесь и в дальнейшем 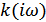заменено на 
).
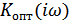Подставляя в левую часть формулы (9.30)
получаем:
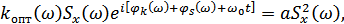
или, сокращая на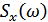 
:
Последнюю формулу можно представить в виде двух составляющих, позволяющих найти амплитудно-частотную характеристику (АЧХ) оптимального (или согласованного) фильтра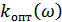 
и фазо-частотную характеристику 
:
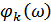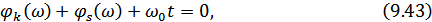
откуда:
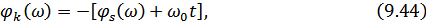
здесь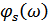 
– фазо-частотный спектр входного сигнала,
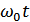– запаздывающий множитель, учитывающий то, что «отсчет» величины сигнала на выходе фильтра производится в момент 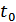, когда возникает максимум выходного сигнала фильтра.
Условие (9.41) имеет простой смысл: фильтр должен лучше пропускать составляющие спектра сигнала, имеющие большую амплитуду, и в меньшей степени пропускать составляющие сигнала, имеющие меньшую амплитуду.
Условие (9.42) также имеет простой смысл: в момент отсчета 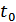все составляющие спектра выходного сигнала имеют нулевую фазу, благодаря чему выходное напряжение в момент 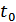имеет наибольшее отношение мощности сигнала к мощности помехи.
Условия (9.43) и (9.44) можно объединить в одно, представив передаточную характеристику в комплексной форме:
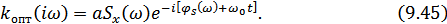
Можно, наконец, последнюю формулу представить в следующем виде:
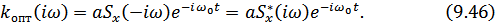
Здесь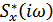 
– колмплексно-сопряженный спектр по отношению к 
.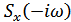