Частные случаи приемника Котельникова

Дата: 2025-06-02; Просмотры: 16
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

1. Оптимальный приемник Котельникова для сигналов с пассивной паузой.

 

 

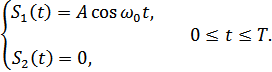
Если

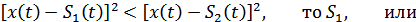
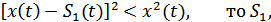
т.к.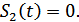

Или, раскрывая квадратную скобку и выполняя элементарные преобразования, можно получить:

 

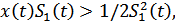
в интегральной форме:

 

 

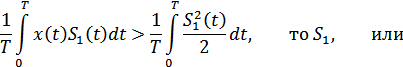
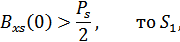
где 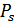– мощность сигнала.

Рисунок 9.6. Структурная схема приемника ДАМ

 

Для реализации идеального приемника Котельникова нужно на приеме знать мощность сигнала. Если 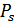меняется, то такой приемник не реализуется.

 

2. Оптимальный приемник Котельникова для сигналов с активной паузой (дискретная частотная и фазовая модуляции).

ДЧМ:

 

 

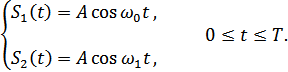
ДФМ:

 

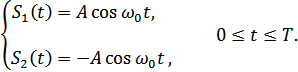
Тогда, если , то .

 

Раскрывая квадратные скобки и выполняя элементарные преобразования с учетом 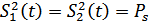, окончательно получим:

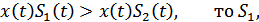
или в интегральной форме

 

 

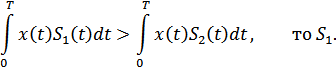
Интегралы представляют собой функции корреляции входного сигнала с одним из опорных, тогда можно записать:

 

Если , .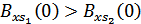

 

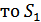Если фаза опорного генератора 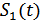совпадает с фазой приходящего сигнала 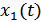, получим когерентный корреляционный приемник.

Рисунок 9.7. Структурная схема корреляционного приемника для ДФМ

 

Для ДФМ схема может быть упрощена (сигналы отличаются знаком амплитуды).

 

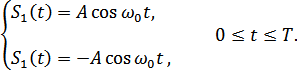
Рисунок 9.8. Структурная схема приемника ДФМ

9.4. Вероятность ошибки в приемнике Котельникова (общий случай и частные случаи)

 

Определим вероятность ошибки в системе передачи двоичных сигналов при приеме на оптимальный приемник. Эта вероятность, очевидно, будет минимально возможной и будет характеризовать потенциальную помехоустой­чи­вость при данном способе передачи.

 

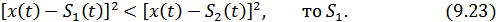
Ошибка произойдет, если при передаче неравенство превращается в противоположное. Приемник принимает 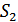при передаче .

 

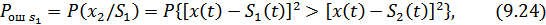
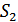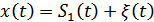получили при передаче . Подставляя в (9.24) , получим:

 

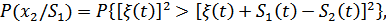
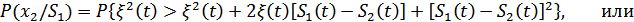
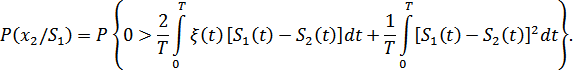
Введя некоторые обозначения, можно получить:

 

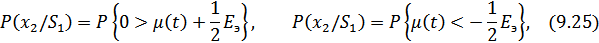
где 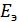– эквивалентная энергия разности сигналов ,

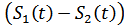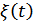– аддитивная помеха.

 

 

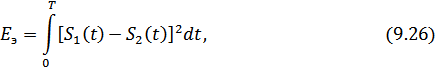
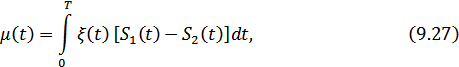
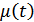– случайная величина, т.к. зависит от .

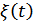Средняя вероятность ошибки определяется следующим выражением:

 

 

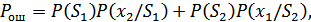
если канал симметричный, т.е.:

 

 

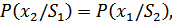
тогда:

 

 

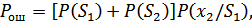
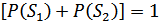– сумма вероятностей для полной группы событий. Тогда:

 

 

Пусть 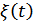распределена по нормальному закону. Тогда и 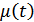распределена по нормальному закону, т.к. линейное преобразование нормального процесса дает нормальный процесс.

 

 

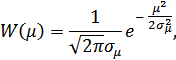
математическое ожидание 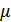равно 0.

Можно показать, что 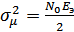, где 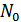– спектральная плотность.

 

 

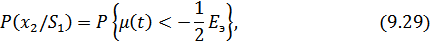
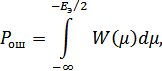
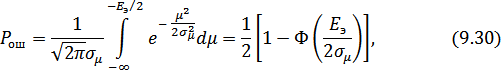
где 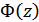– интеграл вероятностей (табулированная функция):

 

 

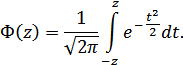
Раскрывая аргумент интеграла вероятности:

 

 

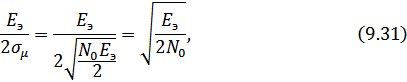
окончательно получаем

 

 

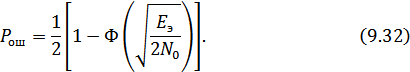
Формула (9.32) является достаточно общей. Для конкретных видов модуляции в канале связи эту формулу видоизменяют, для чего вычисляют соответствующее значение 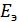. При этом для различных видов модуляции 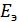определяется через энергию одного из сигналов, а в окончательную формулу вводят величину

 

 

Следовательно, в приемнике Котельникова, который также называется когерентным (в приемнике известна фаза принимаемого сигнала), вероятность ошибки зависит не от отношения мощности сигнала к мощности помехи, а от отношения энергии сигнала к спектральной плотности помехи. Это позволяет, не меняя мощности сигнала, увеличить его энергию за счет увеличения его длительности, что дает дополнительные возможности в построениии помехоустойчивых систем связи. Иначе говоря, в идеальном приемнике Котельникова 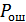зависит от 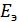и 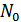(спектральная плотность помехи) и не зависит от полосы пропускания приемника.

 

 

9.5. Частные случаи