Возьмем отсчетов сигнала через одинаковые интервалы , равные интервалу корреляции помехи .
В первом сечении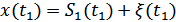 
;
Во втором случае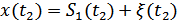 
;
…
В k-ом сечении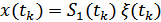 
.
Рисунок 9.4. Сигнал на входе приемника
Рассмотрим отсчетные значения суммы сигнала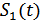 
и помехи 
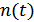в различных сечениях 
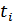. Т.к. расстояние между сечениями равно интервалу корреляции помехи, эти сечения не коррелированны. А т.к. помеха распределена по гауссовскому закону, то эти сечения также и независимы.
Плотность вероятности случайной величины 
в k-ом сечении при известном сигнале 
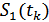определяется выражением
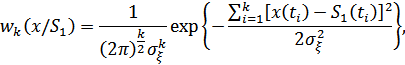
а k-мерная плотность вероятности благодаря независимости сечения будет равна произведению одномерных плотностей вероятностей различных сечений.
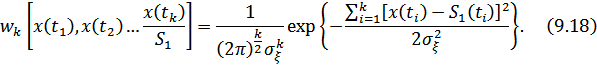
Аналогичное выражение можно записать для сигнала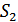 
, заменив в последнем выражении 
на .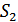
Тогда отношение правдоподобия
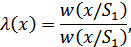
и, согласно правилу решения (9.8), если вычисленное значение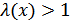 
(у нас 
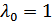), то приемник должен выдать сигнал , в противоположном случае – сигнал 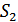. Отсюда получаем оптимальное правило решения в виде неравенства
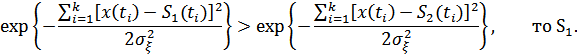
Прологарифмируем это выражение:
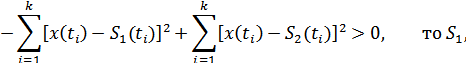
или в другом виде
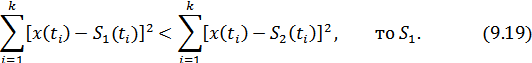
Таким образом, оптимальный приемник (идеальный приемник Котельни-кова) работает следующим образом: определяется среднеквадратическое отклонение поступившего на его вход сигнала 
от обоих ожидаемых сигна-лов и выносится решение пользу того сигнала, где это среднеквадратическое отклонение меньше.
Если при вычислении условных вероятностей расстояние между сечениями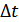 
устремить к нулю, т.е. сделать 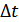меньше интервала корреляции помехи, работа приемника не улучшиться, т.к. соседние сечения будут сильно коррелированы, но и не ухудшится. Поэтому в правиле решения (9.19) можно заменить суммирование интегрированием.
В интегральной форме получим
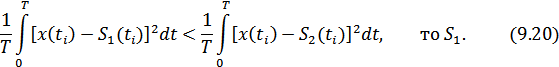
или более компактно (черта означает усреднение по времени)
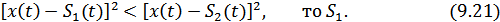
В соответствии с полученным правилом решения структурная схема приемника будет иметь вид, приведенный на рис. 9.5. Схема содержит два генератора опорных сигналов: 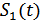и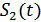 
, которые генерируют точно такие же сигналы, которые могут поступить на вход приемника, а также два вычитающих устройства, два квадратора, два интегратора и схему сравнения, которая, в соответствии с неравенством (9.21), выдает сигналы и .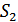
При этом следует подчеркнуть, что приемник Котельникова, как и многие другие приемники дискретных сигналов, выдает на выходе сигналы (решения), форма которых обычно отличается от формы сигналов в линии связ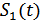и и 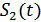. Например, в линии связи эти сигналы могут представлять собой импульсы дискретной частотной модуляции, а на выходе приемника получаем импульсы постоянного тока прямоугольной формы.
Если вероятности передачи сигналов 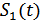и 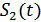не одинаковы, т.е. 
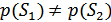, то неравенство (9.21) принимает несколько другой вид
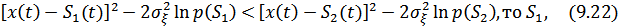
а в структурной схеме перед схемой сравнения добавляются выравнивающие устройства – В (показаны пунктиром).
Может показаться, что приведенная на рисунке схема приемника достаточно проста. Однако применяющиеся в схеме местные генераторы 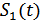и 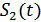должны выдавать сигналы, по форме идентичные передаваемым сигналам, ожидаемым на входе приемника; поэтому эти генераторы должны синхронизироваться приходящими сигналами, а это сделать довольно трудно.
Рисунок 9.5. Структурная схема оптимального приемника Котельникова