Оптимальной решающей схемой будет такая, которая обеспечивает минимум среднего риска. Критерий минимального риска относится к классу так называемых байесовых критериев.

Дата: 2025-06-02; Просмотры: 17
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

В радиолокации широко используется критерий Неймана-Пирсона. При выборе этого критерия учитывается, во-первых, что ложная тревога и пропуск цели не являются равноценными по своим последствиям, и, во-вторых, что неизвестна априорная вероятность передаваемого сигнала. Если пропуск цели является более нежелательным, то можно задать некоторую величину 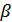допустимой вероятности ложной тревоги и потребовать, чтобы решающая система максимизировала вероятность правильного обнаружения 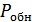(или, что то же самое, минимизировала вероятность пропуска ).

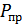Согласно критерию Неймана-Пирсона приемник является оптимальным в том случае, если при заданной вероятности ложной тревоги

 

 

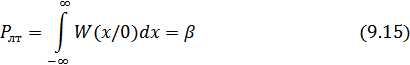
он обеспечивает наибольшую вероятность правильного обнаружения:

 

 

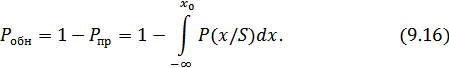
Можно показать, что критерий Неймана-Пирсона приводит к следующему правилу решения: цель считается обнаруженной, если

 

 

где – некоторое число, определяемое допустимой вероятностью ложной тревоги .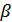

 

 

9.3. Оптимальный приемник полностью известных сигналов. Приемник Котельникова

Рассмотрим систем у передачи информации, в которой передаются два сигнала 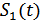и 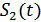одинаковой длительности 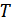, произвольной (но известной) формы, априорные вероятност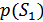и и 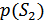; помехи в канале флуктуацион­ные, ФВП которых имеет вид гауссовского закона

 

 

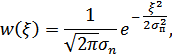
где 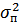– дисперсия (мощность) помех.

Задан критерий оптимального приема: идеальный наблюдатель (или наблюдатель В.А.Котельникова), который минимизирует среднюю вероятность ошибки

 

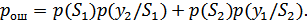
Найдем оптимальное правило решения и структурную схему оптималь­ного приемника (оптимального РУ) для указанных выше условий передачи сигналов 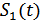и .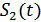

1. Для решения задачи используем общее для приемников двоичных сигналов правило решения (9.7). В рассматриваемом случае

 

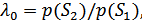
Если 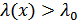, то принимается решение в пользу сигнала , иначе .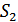

 

Для упрощения решения положим вначале, что 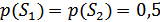; тогда 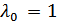. В этом случае критерий идеального наблюдателя совпадает с критерием максимального правдоподобия.

2. Для определения функции правдоподобия 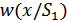и 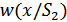, которые при произвольной длительности сигналов 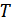будут многомерными. Предположим, что на вход приемника поступает сигнал

 

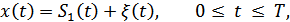
например, рис. 9.4.