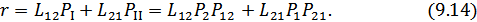Таким образом, критерий идеального наблюдателя сводится к сравнению отношений правдоподобия (9.8). Этот критерий является более общим и называется критерием максимального правдоподобия.

Дата: 2025-06-02; Просмотры: 15

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

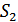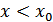Рассмотрим бинарную систему, в которой передача сообщений осуществляется с помощью двух сигналов и . Решение принимается по результату обработки принятого колебания пороговым методом: регистрируется , если , и 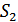, если 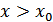, где 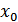– некоторый пороговый уровень . Здесь могут быть ошибки двух видов: воспроизводится , когда передавался 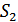, и s2, когда передавался . Условные вероятности этих ошибок (вероятности переходов) будут равны:

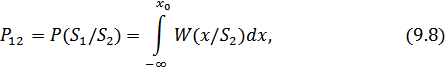
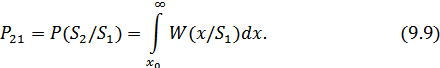
Значения этих интегралов могут быть вычислены как соответствующие площади, ограниченные графиком плотностей условного распределения вероятностей (рис. 9.3).

Рисунок 9.3. ФПВ гауссовского закона при нулевом и ненулевом мат. ожидании

Вероятности ошибок первого и второго вида соответственно:

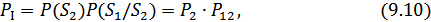
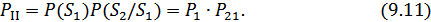
Полная вероятность ошибки при этом

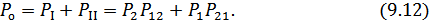
Пусть 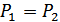, тогда:

Нетрудно убедиться, что в этом случае минимум 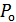имеет место при 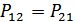, т.е. при выборе порога в соответствии с рис. 9.3. Для такого порога 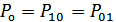. На рис. 9.3 значение 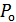определяется заштрихованной пло­щадью. При любом другом значении порога величина 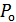будет больше.

Несмотря на естественность и простоту, критерий Котельникова имеет недостатки. Первый заключается в том, что для построения решающей схемы, как это следует из соотношения (9.4), необходимо знать априорные вероятности передачи различных символов кода. Вторым недостатком этого критерия является то, что все ошибки считаются одинаково нежелательными (имеют одинаковый вес). В некоторых случаях такое допущение не является правильным. Например, при передаче чисел ошибка в первых значащих цифрах более опасна, чем ошибка в последних цифрах. Пропуск команды или ложная тревога в различных системах оповещения могут иметь различные последствия.

Следовательно, в общем случае при выборе критерия оптимального приема необходимо учитывать те потери, которые несет получатель сообщений при различных видах ошибок. Эти потери можно выразить некоторыми весовыми коэффициентами, приписываемыми каждому из ошибочных решений. Обозначим потери ошибочных решений первого и второго видов соответственно 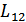и 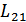. Тогда можно определить средние ожидаемые потери или средний риск: