Если для решения своей задачи приемник использует все параметры сигнала, не несущие информацию, то он называется приемником полностью известного сигнала.
Если эта задача решается наилучшим образом по сравнению с другими приемниками, то такой приемник называется оптимальным или приемником, реализующим потенциальную помехоустойчивость («идеальный приемник»).
Потенциальная помехоустойчивость впервые была определена в 1946 году В.А.Котельниковым в условиях гауссовских помех. Согласно теории потенциальной помехоустойчивости любая система передачи информации с заданным ансамблем сигналов в условиях конкретных помех имеет предельную помехоустойчивость, которая не может быть улучшена путем совершенствования приемника, и поэтому называется потенциальной помехоустойчивостью.
Если для определения информационного параметра используются не все параметры сигнала, не несущие информацию, то это приемник не полностью известного сигнала. Такой приемник также может быть оптимальным (лучшим среди этого класса приемников), но его помехоустойчивость всегда ниже потенциальной. В зависимости от назначения системы связи задачи приемника классифицируются следующим образом.
1. Обнаружение сигнала. При этом приемник решает, есть на его входе сигнал (вместе с помехой), или же на его входе имеется только одна помеха. Сам сигнал заранее известен. На рис. 9.1 в некотором пространстве (система координат 1, 2) изображен вектор сигнала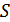 
, на который накладываются векторы помех с различными фазами и амплитудами (в любой момент времени к вектору сигнала добавляется один из векторов помех). Если сигнал 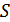на входе приемника отсутствует, векторы помех исходят из начала координат.
Рисунок 9.1. Влияние помех при:
а) обнаружении сигнала;
б) различении сигналов
Для решения вопроса о наличии или отсутствии сигнала на входе приемника все пространство разбивается на два подпространства: подпространство сигнала и подпространство помех. В зависимости от того, в какое подпространство попадает конец результирующего вектора, приемник выполнит решение о наличии или отсутствии сигнала на его входе. Границы подпространств на рисунках показаны пунктиром. Если под действием помехи конец суммарного вектора попадает в подпространство помех, имеет место пропуск сигнала; если, наоборот, конец вектора помехи без сигнала попадает в подпространство сигнала, имеет место ложная тревога.
2. Различение двух сигналов (или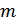 
сигналов). Приемник решает, какой из сигналов ( 
или 
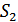) имеется на его входе. Все пространство сигналов и помех разбивается на подпространства по числу сигналов (в данном случае на два). Приемник принимает решение в пользу того сигнала, в подпространстве которого находится конец вектора суммы сигнала и помехи. Если под действием помехи конец суммарного вектора попадет в чужое подпространство, произойдет ошибка.
Следует иметь в виду, что, когда приемник предназначен для приема дискретных сигналов (обнаружение сигналов, различение сигналов), то, как правило, форма выходных сигналов не совпадает с формой сигналов на его входе. Например, если приемник осуществляет различение сигналов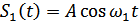 
и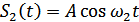 
(дискретная частотная модуляция), то при приеме сигнала 
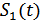на выходе приемника будет импульс напряжения положительной полярности, а при приеме сигнала 
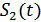– импульс отрицательной полярности (или 0, в зависимости от конкретной реализации схемы приемника).
3. Оценка параметров сигнала – например, его амплитуды или величины запаздывания – применяется в телеметрических системах, в радиолокации; при этом скорость изменения измеряемого параметра сигнала значительно меньше скорости измерения (значение параметра не изменяется в процессе измерения).
4. Восстановление формы переданного сигнала осуществляется при приеме аналоговых сигналов (фильтрация), и в отличие от оценки параметров измеряемый параметр непрерывно меняется в процессе измерения. Таким образом, приемник представляет собой решающее устройство, которое в соответствии с некоторым правилом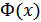 
(правило решения) определяет значение информационного параметра (принимает решение о значении выходного сигнала 
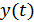, используя входной сигнал 
).
Рисунок 9.2. Сущность восстановления формы сигнала
9.2. Критерии приема дискретных сигналов. Отношение правдоподобия
Выбор критерия оптимальности не является универсальным, он зависит от поставленной задачи и условий работы системы связи.
Пусть на вход приемника поступает сумма сигнала и помехи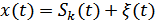 
, где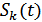 
– сигнал, которому соответствует кодовый символ 
, 
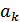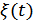– аддитивная помеха с известным законом распределения. Сигнал 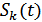в месте приема является случайным с априорным распределением 
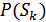. На основании анализа колебания приемник воспроизводит сигнал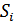 
. При наличии помех это воспроизведение не может быть совершенно точным. По принятой реализации сигнала приемник вычисляет апостериорное распределение 
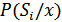, содержащее все сведения, которые можно извлечь из принятой реализации сигнала . Теперь необходимо установить критерий, по которому приемник будет выдавать на основе апостериорного распределения 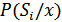решения относительно переданного сигнала 
.
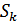1. При передаче дискретных сообщений широко используется критерий Котельникова (критерий идеального наблюдателя). Согласно этому критерию принимается решение, что передан сигнал 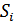, для которого апостериорная вероятность 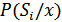имеет наибольшее значение, т. е. регистрируется сигнал 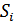, если выполняется неравенство:
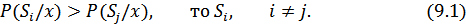
При использовании такого критерия полная вероятность ошибочного решения будет минимальной. Действительно, если по сигналу 
принимается решение о том, что был передан сигнал 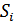, то, очевидно, вероятность правильного решения будет равна 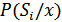, а вероятность ошибки – 
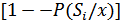. Отсюда следует, что максимуму апостериорной вероятности 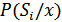соответствует минимум полной вероятности ошибки 
:
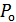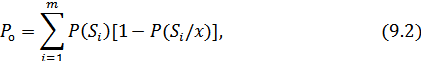
где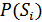 
– априорные вероятности передаваемых сигналов.
На основании формулы Байеса:
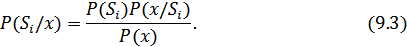
Тогда неравенство (9.1) можно записать в другом виде:
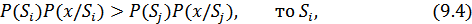
или
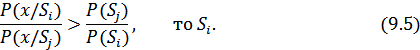
Функцию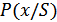 
часто называют функцией правдоподобия. Чем больше значение этой функции при данной реализации сигнала , тем правдоподобнее, что передаваемый сигнал – 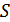. Отношение, входящее в неравенство (9.5)
называется отношением правдоподобия. Пользуясь этим понятием, правило решения (9.5), соответствующее критерию Котельникова, можно записать в виде:
Если передаваемые сигналы равновероятны: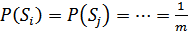 
, то это правило решения принимает более простой вид:
