Сосредоточенные (по спектру) помехи – это помехи от посторонних радиостанций или генераторов высокой частоты. Они имеют узкий спектр по сравнению с полосой пропускания канала связи.
Рисунок 8.58. Представление сосредоточенной помехи
Избавляются от них с помощью заграждающих фильтров или используют широкополосные сигналы.
Мультипликативная помеха
Мультипликкативные помехи – помехи, которые не складываются с сигналом, а умножаются на сигнал:
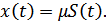
Рисунок 8.59. Возникновение замираний из-за многолучевости
Сигналы в точку приема 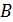 приходят по разным траекториям, т.е. с разной задержкой, а значит, с разными фазами. Если фазы приходящих сигналов совпадают – получается максимум, если приходят в противофазе – минимум. Непостоянства амплитуды сигнала называются замираниями. Замирания подразделяются на медленные и быстрые. Медленные – такие, для которых время замирания велико по сравнению с длительностью элементарного сигнала. С ними борются, используя автоматическую регулировку усиления в аппаратуре связи.
приходят по разным траекториям, т.е. с разной задержкой, а значит, с разными фазами. Если фазы приходящих сигналов совпадают – получается максимум, если приходят в противофазе – минимум. Непостоянства амплитуды сигнала называются замираниями. Замирания подразделяются на медленные и быстрые. Медленные – такие, для которых время замирания велико по сравнению с длительностью элементарного сигнала. С ними борются, используя автоматическую регулировку усиления в аппаратуре связи.
Быстрые замирания – такие, для которых время замираний соизмеримо (или меньше) длительности элементарного сигнала. С ними борются путем применения помехоустойчивого кодирования. Сигнал на входе приемника в общем случае имеет вид:
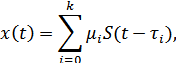
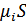 – амплитуда сигнала, прошедшего по
– амплитуда сигнала, прошедшего по 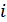 -му пути,
-му пути,
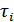 – время запаздывания
– время запаздывания 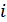 -го луча.
-го луча.
Если 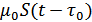 – основная (стационарная) составляющая, то:
– основная (стационарная) составляющая, то:
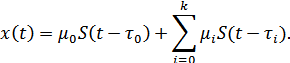
При большом 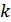 (
( 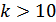 ) считают, что рассеянная составляющая распределена по нормальному закону и рассматривается как флуктуационная помеха. При этом огибающая помехи распределена по рэлеевскому закону. Поэтому замирания с нормальным законом распределения называется рэлеевскими замираниями.
) считают, что рассеянная составляющая распределена по нормальному закону и рассматривается как флуктуационная помеха. При этом огибающая помехи распределена по рэлеевскому закону. Поэтому замирания с нормальным законом распределения называется рэлеевскими замираниями.
8.16. Геометрическое представление сигналов и помех
Совокупность трех чисел 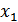 ,
, 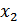 ,
, 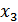 может быть представлена как координаты вектора в трехмерном пространстве. Аналогично
может быть представлена как координаты вектора в трехмерном пространстве. Аналогично 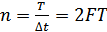 отсчетов, определяющих сигнал, можно представить себе как координаты вектора в воображаемом
отсчетов, определяющих сигнал, можно представить себе как координаты вектора в воображаемом  -мерном пространстве.
-мерном пространстве.
Свойства  -мерного пространства в значительной степени являются обобщением свойств двух- и трехмерного пространств. Длина (
-мерного пространства в значительной степени являются обобщением свойств двух- и трехмерного пространств. Длина ( 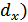 вектора
вектора 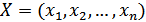 определяется его нормой
определяется его нормой 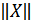 :
:
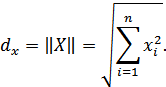
Таблица 8.1 – Параметры векторов в непрепывном и дискретном пространствах.
| Параметры | Эвклидово пространство, n-конечно | Гильбертово пространство, n-бесконечно |
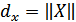 (длины вектора)
(длины вектора)
| 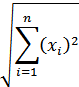
| 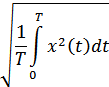
|
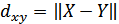 (расстояние между векторами)
(расстояние между векторами)
| 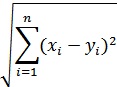
| 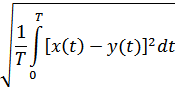
|
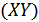 (скалярное произведение)
(скалярное произведение)
| 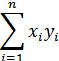
| 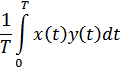
|
Фазовый сдвиг 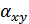 между
между 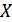 и
и 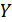 :
:
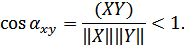
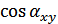 не может быть больше 1:
не может быть больше 1:
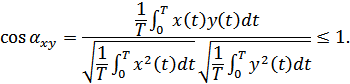
Неравенсво Шварца-Буниковского:
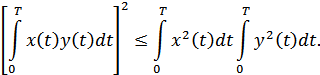
Расстояние между двумя векторами  и
и 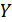 определяется как норма разности векторов:
определяется как норма разности векторов:
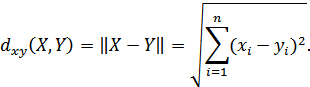
Скалярное произведение двух векторов:
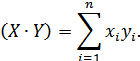
Координаты вектора 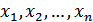 представляют собой проекцию вектора
представляют собой проекцию вектора 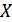 на оси. Если обозначить угол мнежду векторами через
на оси. Если обозначить угол мнежду векторами через 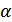 , то получим выражение (фазовый сдвиг):
, то получим выражение (фазовый сдвиг):
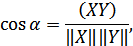
а для проекций 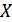 на
на  и обратно
и обратно  на
на  :
:
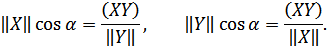
Пространство непрерывных функций (сигналов), заданных на интервале 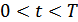 , имеет бесконечное число измерений. Для такого пространства скалярное произведение двух векторов определяется соотношением (функция взаимной корреляции):
, имеет бесконечное число измерений. Для такого пространства скалярное произведение двух векторов определяется соотношением (функция взаимной корреляции):
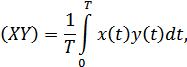
а норма и расстояние между векторами:
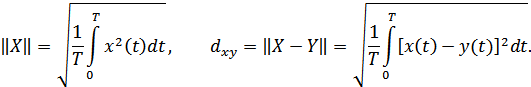
Пространство с бесконечным числом измерений прдставляет собой естественное обобщение  -мерного пространства, полученного путем предельного перехода от дискретной последовательности к функции непрерывного аргумента. Отметим, что нормы векторов равны корням из их мощностей, а скалярное произведение является мерой корреляции этих сигналов. Сигналы конечной длительности
-мерного пространства, полученного путем предельного перехода от дискретной последовательности к функции непрерывного аргумента. Отметим, что нормы векторов равны корням из их мощностей, а скалярное произведение является мерой корреляции этих сигналов. Сигналы конечной длительности 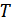 , ограниченные полосой
, ограниченные полосой 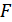 , геометрически представляются различными векторами в n-мерном пространстве. Различие между двумя какими-либо сигналами выражается расстоянием между векторами. Это расстояние зависит от длин векторов и угла между ними, а косинус
, геометрически представляются различными векторами в n-мерном пространстве. Различие между двумя какими-либо сигналами выражается расстоянием между векторами. Это расстояние зависит от длин векторов и угла между ними, а косинус 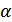 есть не что иное, как коэффициент взаимной корреляции сигналов.
есть не что иное, как коэффициент взаимной корреляции сигналов.
Рисунок 8.60. Векторное представление сигналов и помехи
Полное отсутствие корреляции (т.е. равенство нулю коэффициента корреляции) выражается ортоганальностью векторов ( 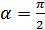 ).
).
Помеха, ограниченная той же полосой, что и сигнал, также определяется вектором в n-мерном пространстве. Этот вектор добавляется к вектору сигнала. В отличие от вектора сигнала, вектор помехи может иметь любые величину и направление (вектор случайный). В результате при наложении помехи на сигнал вокруг конца вектора сигнала образуется «облако», переменная плотность которого выражает вероятность попадания результрующего вектора 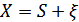 (вектор принятого сигнала) в данный элемент объема. Для флуктуационной помехи это «облако» имеет сферическую форму с эффективным радиусом
(вектор принятого сигнала) в данный элемент объема. Для флуктуационной помехи это «облако» имеет сферическую форму с эффективным радиусом
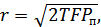
где 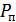 – мощность помехи.
– мощность помехи.
Сообщение (видиосигнал) 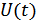 , не содержащее колебаний с частотой выше
, не содержащее колебаний с частотой выше 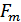 , так же, как и сигнал, может быть представлено в m-мерном пространстве, где
, так же, как и сигнал, может быть представлено в m-мерном пространстве, где 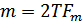 . Совокупность возможных сообщений определяет это пространство (пространство сообщений). На следующем рисунке представлена двухмерная модель этого пространства и двумя различными сообщениями
. Совокупность возможных сообщений определяет это пространство (пространство сообщений). На следующем рисунке представлена двухмерная модель этого пространства и двумя различными сообщениями 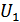 и
и 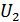 .
.
Рисунок 8.61. Векторное представление сигналов и помехи
При передаче сообщения 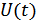 преобразовывается в сигнал
преобразовывается в сигнал  с использованием некоторого переносчика
с использованием некоторого переносчика 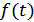 . Математически эту операцию формирования сигнала можно представить в виде
. Математически эту операцию формирования сигнала можно представить в виде
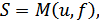
где 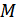 – оператор, в общем случае нелинейный. Теоретически формирование сигнала может быть представлено как преобразование пространства сообщений
– оператор, в общем случае нелинейный. Теоретически формирование сигнала может быть представлено как преобразование пространства сообщений 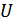 в пространство сигналов
в пространство сигналов 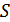 : векторы
: векторы 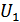 и
и 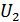 преобразуются в векторы
преобразуются в векторы  и
и 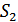 .
.
Мерность пространства сообщений 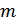 в общем случае не равна мерности сигналов
в общем случае не равна мерности сигналов  . При однополосной передаче
. При однополосной передаче 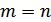 . В случае амплитудной модуляции сигналы имеют вдвое большее число координат, чем сообщений:
. В случае амплитудной модуляции сигналы имеют вдвое большее число координат, чем сообщений: 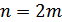 , а при частотной пространство сигналов имеет значительно большее число измерений, чем пространство сообщений.
, а при частотной пространство сигналов имеет значительно большее число измерений, чем пространство сообщений.
При наложении помехи на сигнал создается область неопределенностей, в которую попадают принятые сигналы 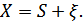 Взаимодействие сигнала и помехи можно выразить оператором
Взаимодействие сигнала и помехи можно выразить оператором 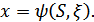
Оператор 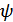 преобразует пространство сигналов
преобразует пространство сигналов 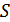 в пространство принятых сигналов
в пространство принятых сигналов 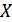 : векторы
: векторы  и
и 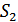 переходят в
переходят в 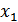 и
и 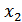 .
.
Приемник по принятым сигналам  воспроизводит переданное сообще-ние
воспроизводит переданное сообще-ние 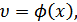 т.е. преобразует пространство сигналов
т.е. преобразует пространство сигналов 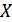 в пространство принятых сообщений
в пространство принятых сообщений 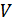 .
.
Если помеха отсутствует, то принятый сигнал преобразуется в сообщение обратным оператором 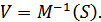 В этом случае принятие сообщения соответствует (тождественно) переданному.
В этом случае принятие сообщения соответствует (тождественно) переданному.
При наличии помех сообщения на приеме воспроизводятся с ошибкой, вместо 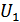 может быть воспроизведено
может быть воспроизведено 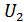 и наоборот. Ошибка произойдет, когда результирующий вектор
и наоборот. Ошибка произойдет, когда результирующий вектор 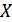 окажится ближе к концу вектора того сигнала, который в данный момент не передается. Можно построить приемник, воспро-изводящий сообщение
окажится ближе к концу вектора того сигнала, который в данный момент не передается. Можно построить приемник, воспро-изводящий сообщение 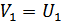 всякий раз, когда конец вектора
всякий раз, когда конец вектора 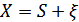 бли-же к концу вектора
бли-же к концу вектора  , чем к концу вектора
, чем к концу вектора 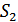 и наоборот. Такой приемник по Котельникову называется идеальным или оптимальным. Очевидно, ошибка при оптимальном приеме будет тем меньше, чем больше расстояние
и наоборот. Такой приемник по Котельникову называется идеальным или оптимальным. Очевидно, ошибка при оптимальном приеме будет тем меньше, чем больше расстояние 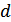 между соседними сигналами.
между соседними сигналами.
9. Основы теории помехоустойчивости
9.1. Задачи приемного устройства
На вход приемного устройства (приемника) любой системы связи обычно поступает смесь переданного сигнала  и помехи
и помехи 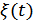 :
:
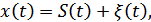
причем сигнал  представляет собой, как правило, сложные колебания, содержащие, кроме времени
представляет собой, как правило, сложные колебания, содержащие, кроме времени 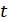 , множество параметров (амплитуду, фазу, частоту и пр.):
, множество параметров (амплитуду, фазу, частоту и пр.): 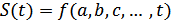 . Один или группа этих параметров используется для передачи информации, а задачей приемника является определение (измерение) этих параметров в условиях мешающего действия помех.
. Один или группа этих параметров используется для передачи информации, а задачей приемника является определение (измерение) этих параметров в условиях мешающего действия помех.








