Встречаются каналы, в которых сигнал в точку приема приходит по различным путям с различными затуханиями и запаздываниями .Такие каналы называются многопутевыми или многолучевыми.
Сигнал на выходе канала можно записать в виде:
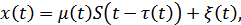
где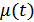 
– затухание сигнала (мультипликативная помеха),
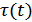– время задержки сигнала,
– сигнал на входе канала,
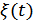– аддитивная помеха,
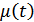и 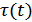могут быть постоянными.
Есл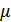и 
и 
фиксированы во времени, то имеем канал с постоянными параметрами. В реальных каналах происходит непрерывное и часто случайное изменение параметров 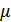и . Такие каналы называются каналами с переменными параметрами.
В канале последовательность входных сообщений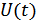 
преобразовывается в последовательность элементов выходного сообщения 
.
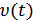В геометрическом представлении это означает преобразование пространства входных сообщений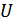 
в пространство выходных сообщений 
.
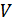При изучении каналов связи иногда удобно рассматривать вместо элементов исходного сигнала последовательность кодовых символов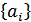 
.
Канал называется дискретным, если пространство входных выходных сигналов дискретны, и непрерывным, если эти пространства непрерывны. Если одно из пространств дискретно, а другое – непрерывно, то канал называется соответственно дискретно-непрерывным или непрерывно-дискретным.
Модели непрерывных каналов связи характеризуются следующими показателями:
1) временем занятия канала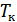 
;
2) шириной полосы пропускания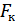 
;
3) динамическим диапазоном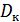 
,
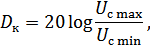
где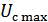 
, 
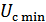– максимальное и минимальное значение сигнала.
Это физические характеристики канала (сигнала). Они взаимосвязаны между собой. Их произведение равно объему канала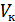 
.
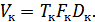
Модель дискретного канала характеризуется следующими показателями:
1. Алфавитом входных и выходных сообщений.
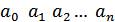– входной алфавит;
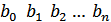– выходной алфавит.
Алфавит выходных сообщений не всегда равен алфавиту входных.
2. Скоростью передачи.
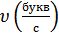или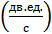 
, [Бод].
3. Априорными вероятностями входных сообщений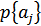 
4. Вероятностями перехода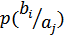 
.
Рассмотрим двоичный дискретный канал (ДДК). Такой канал обычно описывается графиком состояний:
Рисунок 8.41. Граф состояний ДДК
Если передали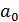 
и получили 
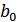, то это верная передача. Если передали 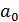, а получили (под воздействием помех) 
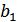, то это ошибка. Аналогичная ошибка – при переходе 
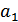в .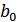
8.14. Классификация дискретных каналов связи
1. Если вероятность перехода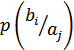 
для каждого 
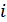и 
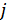не зависит от времени и от того, какие символы предшествовали данному символу, то это однородный канал без памяти (стационарный).
2. Если вероятность перехода зависит от времени, то канал неоднородный (нестационарный). Такие каналы делятся на каналы с памятью и без памяти.
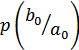– без памяти, 
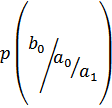– с памятью.
3. Симметричные и несимметричные. В симметричных каналах вероятности переходов попарно равны.
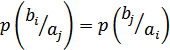– симметричный.
;
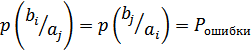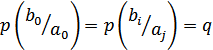– правильный прием.
4. Каналы со стиранием и без стирания. В каналах со стиранием алфавит выходных сообщений на единицу больше, чем алфавит входных.
;
.
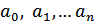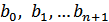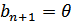– символ стирания.
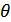выдается приемником тогда, когда решающее устройство приемника не может однозначно решить, какой сигнал поступил на его вход.
Поясним сказанное на примере наиболее простого и, в то же время, наиболее распространенного на практике двоичного канала.
Рассмотрим двоичный канал, построенный следующим образом. Дискретный модулятор при подаче на его вход символа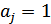 
выдает положительный импульс постоянного напряжения величины 
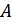(являющийся элементарным сигналом 
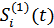), а при передаче символа 
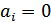– отрицательный импульс постоянного напряжения 
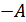(являющийся элементарным сигналом 
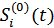). Образованный таким образом сигнал , отображающий последовательность символов 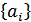, поступает на вход гауссовского канала с полосой пропускания от 0 до 
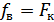. Если 
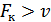, то сигнал на входе решающего устройства:
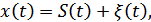
где 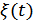– помеха, имеющая нормальное распределение с нулевым срезом:
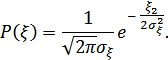
Рисунок 8.42. Временная характеристика двуполярной последовательности импульсов
Рисунок 8.43. Сущность работы РУ без стирания и со стиранием
Пусть решающее устройство (РУ) принимает решение на основе сравнения однократного отсчета каждого принимаемого импульса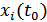 
с пороговым значением 
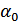: если отсчет 
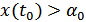превышает порог 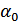, то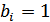 
, если 
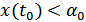, то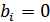 
. В зависимости от значения помехи 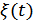в момент отсчета решение может быть правильным или неправильным. При скорости передачи 
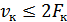интервал между отсчетами 
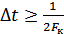и отсчеты помехи независимы. Таким образом, описанный канал является стационарным (в силу стационарности гауссовой помехи) двоичным каналом без памяти.
Очевидно, что переданный символ 0 будет принят решающим устройством как 1, если значение помехи в момент отсчета превысит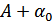 
(рис. 8.43). Поэтому
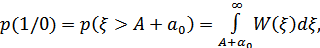
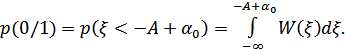
Рисунок 8.44. Зоны перехода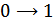 
и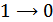 
На рис. 8.44 показаны площади, равные вероятност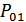и 
и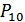 
. В общем случае они не равны. При этом вероятности ошибки:
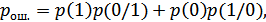
зависит от априорных вероятносте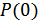й 
и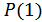 
. Если выбрать пороговое значение 
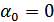, то в силу симметрии распределение 
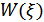относительно оси ординат
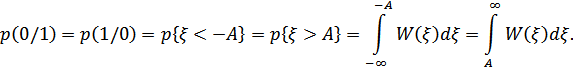
Поэтому для симметричного канала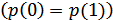 
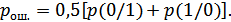
В этом случае при любой статистики входной последовательности:
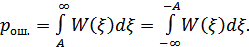
Рисунок 8.45. Определение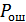 
для симметричного канала
Если, вместо одного порога установить два: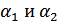 
и принять правило 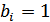, если 
; 
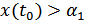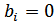, если 
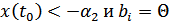, если 
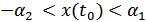, то получим канал со стиранием, в общем случае не симметричный.
Если, однако,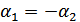 
, то получим симметричный канал со стиранием, причем
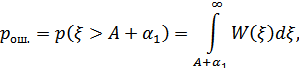
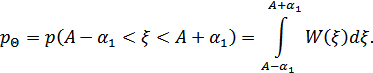
Рисунок 8.46. Определение 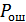для канала со стиранием
Введение стирания позволяет уменьшить вероятность ошибки, но наряду с этим уменьшается вероятность правильного приема
