Поскольку находятся в квадратуре, то будет гипотенузой (рис. 8.33).
Рисунок 8.33. Представление узкополосного СП через квадратурные составляющие
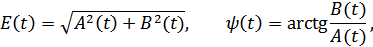
Свойства квадратурных составляющих:
Т.к.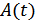 
и 
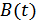являются случайными функциями времени, то законы распределения 
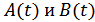совпадают с законом распределения 
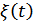, т.е.
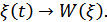
1. 
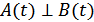, т.е. ортоганальны в совпадающие моменты времени, т.е.
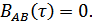
2. 
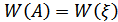и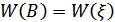 
.
3. 
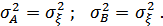
4. 
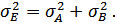Дисперсия огибающей в два раза больше дисперсий составляющих.
Представление случайного процесса квадратурными составляющими имеет большое значение для анализа приемных устройств при когерентном и некогерентном приеме.
8.12. Огибающая и фаза узкополосного гауссовского случайного процесса и суммы гармонического сигнала и узкополосного гауссовского случайного сигнала
1. Огибающая и фаза узкополосного гауссовского случайного процесса.
Рисунок 8.34. Временная и вероятностная характеристики огибающей СП
Если процесс стационарный, то каждую реализацию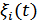 
можно разложить на квадратурные составляющие:
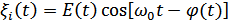
или
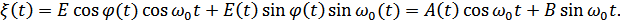
Рисунок 8.35. Разложение огибающей СП на квадратурные составляющие
Считаем, что процесс не содержит постоянной составляющей
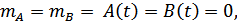
а мощности квадратурных составляющих одинаковы:
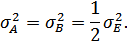
Поскольку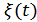 
– нормальный (гауссовский) процесс, то 
, 
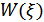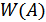и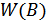 
имеют нормальное распределение:
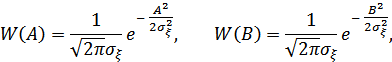
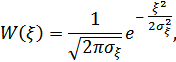
а их функция корреляции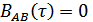 
в совпадающие моменты времени 
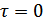. Найдем плотность вероятности огибающей 
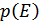и фазы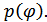 
Рисунок 8.36. Сущность округления огибающей и фазы при нулевой средней
В прямоугольных координатах (рис. 8.36) вероятность того, что случайная величина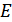 
будет находиться в пределах прямоугольника, ограниченного сторонам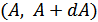и 
и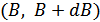 
можно выразить через совместную плотность вероятности:
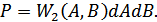
Вероятность этого же события можно записать в полярных координата 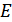и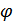 
, т.е.
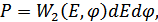
следовательно:
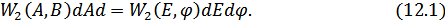
Поскольку речь идет об одной и той же вероятности, то площадь элементарного прямоугольника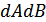 
должна быть равной элементарной площади в полярных координатах:
Кроме того, вследствие статической независимости квадратурных составляющих, а также их 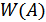и 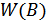, с учетом (12.2):
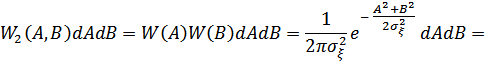
Сопоставляя (12.1) и (12.3), можно получить:
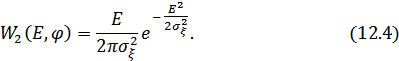
Выражение (12.4) определяет совместную плотность вероятности огибающей 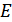и фазы 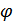. Для определения плотности вероятности огибающей проинтегрируем (12.4) по всем возможным значениям 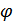в пределах от 0 до 
:
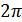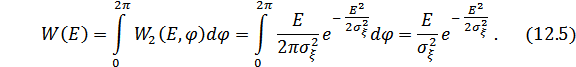
Для определения плотности вероятности фазы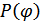 
надо совместную плотность (12.4) проинтегрировать по всем возможным значениям огибающей:
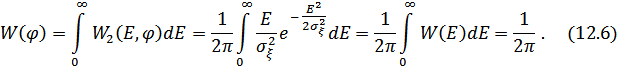
Из (12.6) видно, что плотность вероятности фазы равномерна по всей области возможных значений 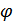от 
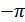до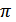 
(рис. 8.37).
Рисунок 8.37. ФПВ огибающей и фазы СП при нулевой средней
Выражение (12.6) может быть безразмерным, если обозначить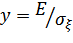 
.
При переходе от 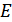к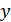 
должно выполняться равенство:
Подставляя в (12.7) значение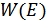 
из (12.5) и учитывая 
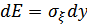, получим:
