1. Математическое ожидание.
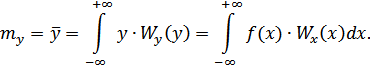
Здесь учтена функциональная связь 
.
2. Дисперсия.
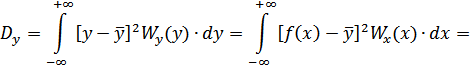
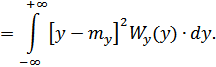
3. Функция корреляции.
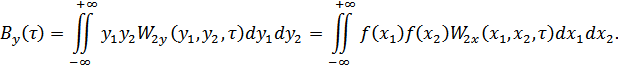
4. Энергетический спектр.
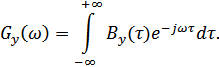
Выводы:
Спектр сигнала на выходе нелинейного элемента отличается от спектра на входе вследствие появления новых частотных составляющих, которые отсутствовали во входном сигнале. Спектр обычно содержит низкочастотные составляющие вблизи нулевой частоты и участки высокочастотных составляющих.
Таким образом, при воздействии случайного процесса на нелинейную систему изменяется спектр процесса, законы распределения вероятностей и все связанные с ними параметры (плотность, мат. ожидание, дисперсия и т.д.).
8.9. Примеры прохождения случайных сигналов через линейные инерционные и нелинейные безинерционные радиотехнические цепи
1. Пусть на вход линейной инерционной цепи с коэффициентом передачи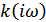 
воздействует «белый» шум с равномерным спектром 
.
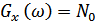Энергетический спектр выходного процесса:
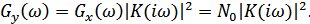
Спектр помехи на выходе цепи в этом случае повторяет по своей форме частотную характеристику цепи с возведенными в квадрат ординатами.
Рисунок 8.23. а) спектр входного сигнала;
б) АЧХ цепи;
в) спектр процесса на выходе ЛИЦ
Мощность шума на выходе при этом равна:
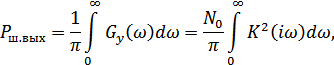
или, вводя эффективную полосу пропускания системы 
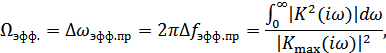
Рисунок 8.24. Сущность округления мощности процесса на выходе ЛИЦ
получаем
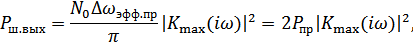
где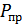 
– мощность процесса в полосе .
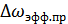Распределение плотности вероятностей случайного процесса (сигнала или помехи) на выходе линейной инерционной системы в общем случае отличается от плотности вероятностей процесса на входе. В одном очень важном случае плотность вероятностей при линейных преобразованиях не изменяется. Это случай гауссовского процесса, т.е. если процесс на входе линейной инерционной системы имеет нормальную плотность вероятностей мгновенных значений, то он остается нормальным и на выходе. Изменяются только параметры процесса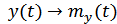 
, 
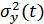(дисперсия или мощность), функция корреляции 
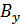(τ) и 
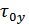в соответствии с 
.
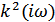2. Теперь рассмотрим прохождение случайного сигнала (процесса) через нелинейную безинерционную цепь.
Сделаем некоторые предварительные замечания:
Рисунок 8.25. Характеристика нелинейной цепи
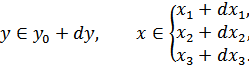
В силу функциональной зависимости:
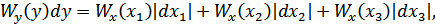
или
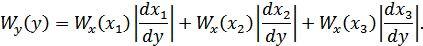
В общем случае:
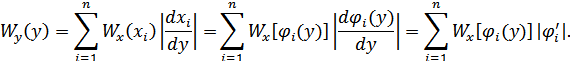
Пример. Рассмотрим определение плотности распределения вероятностей на выходе квадратичного преобразователя с характеристикой:
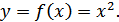
Такое преобразование имеет место, например, в двухполупериодном квадратичном детекторе (рис. 8.26).
Рисунок 8.26. Характеристика квадратичного преобразователя
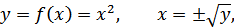
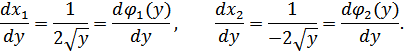
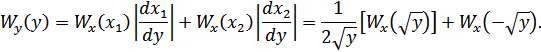
Пусть воздействие имеет нормальное распределение (с нулевым средним):
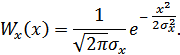
Подставив это выражение вместо плотности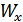 
:
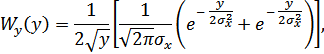
окончательно получим
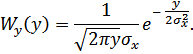
Рисунок 8.27. ФПВ на выходе квадратичного преобразователя
Из рисунка видно, что при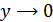 
, 
.
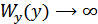8.10. Представление сигнала в комплексной форме. Преобразование Гильберта. Аналитический сигнал
Как детерминированные, так и случайные процессы обычно представляются действительными функциями времени 
. Вместе с тем, часто удобнее представлять их векторами на комплексной плоскости или записывать в символической форме. Напомним смысл широко используемой в теории электрических цепей символической записи синусоидальных колебаний. Практическое значение комплексного представления случайных сигналов: оно позволяет представить любой случайный процесс в виде гармонического колебания со случайной амплитудой огибающей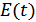 
и фазой 
.
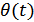Действительная функция:
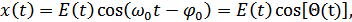
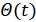– полная фаза,
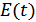– амплитуда (огибающая),
– мгновенная частота,
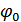– начальная фаза.
В символической форме может быть представлена следующим образом:
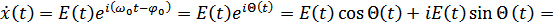
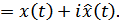
Рисунок 8.28. Сущность округления огибающей СП
Иначе говоря, символическое представление получается добавлением к действительной части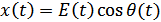 
определенным образом подобранной мнимой части 
.
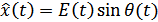Последняя выбирается так, чтобы проекция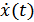 
на ось абсцисс соответствовала исходной действительной функции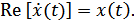 
Рисунок 8.29. Разложение СП на ортогональные составляющие
В нашем случае мнимая часть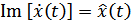 
колебания 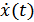находится в квадратуре (сдвинута на угол 
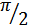) с действительной частью .
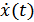Комплексный вектор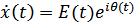 
длиной 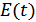вращается с угловой скоростью 
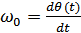против часовой стрелки; конец вектора описывает окружность.
Функции и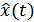 
называются сопряженными по Гильберту. Доказано, что действительная и мнимая составляющая функции связаны между собой парой взаимно однозначных интегральных преобразований Гильберта:
Прямое преобразование Гильберта
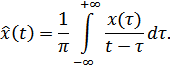
Обратное преобразование Гильберта
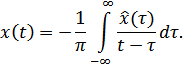
Аналогично для функции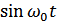 
сопряженной является функция 
.
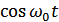Например:
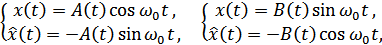
т.е.
Рисунок 8.30. Сущность получения сопряженной по Гильберту функции
Сигнал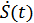 
называется «аналитическим», если 
и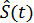 
составляют пару преобразований по Гильберту:
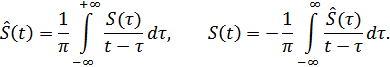
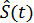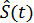Функция называется сопряженной с функцией по Гильберту. При таком выборе и огибающая и фаза сигнала определяются однозначно:
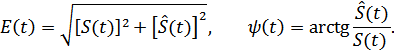
Если эффективная ширина спектра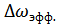 
сигнала мала по сравнению с его частотой , то 
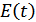и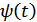 
изменяются медленно по сравнению с функцией . Можно показать, что функции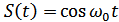 
соответствует сопряженная функция 
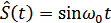, а функции 
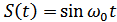соответствует 
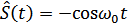. Если исходный сигнал представлен рядом Фурье:
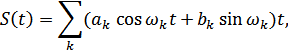
то сопряженный ему ряд:
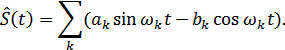
Таким образом, простейшему сигналу в виде гармонического колебания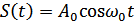 
соответствует аналитический сигнал
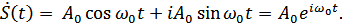
8.11. Комплексное представление узкополосного процесса. Квадратурные составляющие и их свойства
Рисунок 8.31. Эффективная полоса СП
При рассмотрении многих задач удобно выражать сигнал в виде суммы элементарных сигналов, каждый из которых является комплексной функцией времени, либо рассматривать сам сигнал как комплексную функцию:
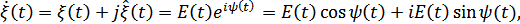
где 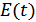и 
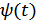– огибающая и фаза сигнала. Действительный сигнал 
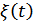в этом случае определяется следующим выражением:
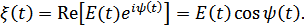
Но
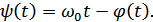
Преобразуя, получим:
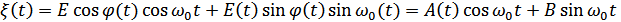
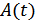
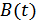
Здесь 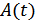и 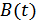– квадратурные составляющие узкополосного случайного процесса.
Вывод:
Любой узкополосный случайный процесс может быть представлен суммой двух гармонических составляющих средней частоты 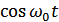и 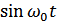со случайными амплитудами и фазами.
Рисунок 8.32. Представление узкополосного СП
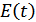и 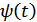в узкополосном сигнале – медленно меняющиеся функции времени по сравнению со средней частотой .
Таким образом, узкополосный случайный процесс можно представить в виде амплитудно-модулированного сигнала со случайной амплитудой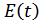 
и случайной фазой 
.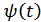