Радиотехнические устройства с точки зрения теории можно подразделить на системы с сосредоточенными параметрами и системы с распределенными параметрами.
Системы с сосредоточенными параметрами (радиотехнические) представляют собой соединения конечного числа элементов цепи. Например, конденсаторов, катушек, сопротивлений. Радиотехническими цепями являются, например, колебательный контур, УНЧ, радиовещательный приемник и т.п.
Системы с распределенными параметрами (радиотехнические) представляют собой соединение бесконечного множества элементов, каждый из которых обладает бесконечно малым параметром. Примерами таких систем является двухпроводная линия, волновод, антенна и т.п.
Мы будем рассматривать только системы с сосредоточенными параметрами.
Элементы радиотехнической цепи можно подразделить на: линейные с постоянными параметрами, линейные с переменными параметрами и нелинейные.
В свою очередь, линейные и нелинейные цепи с постоянными параметрами делятся на инерционные и безинерционные.
Рисунок 8.17. Радиотехнические цепи (РТЦ)
а) линейная безинерционная РТЦ;
б) линейная инерционная РТЦ;
в) нелинейная инерционная РТЦ;
г) нелинейная инерционная РТЦ
Мы будем изучать только линейные инерционные и нелинейные безинерционные цепи.
2. Задачи, решаемые при прохождении случайного процесса через радиотехнические цепи.
Рисунок 8.18. Воздействия и отклики вероятностных и числовых характеристик СП
Решаются 2 типа задач:
1) нахождение плотности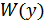 
через 
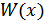и числовых характеристик СП на выходе цепи;
2) нахождение числовых характеристик отклика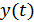 
.
Для линейных инерционных цепей нахождение W(x) – сложная задача, которая, как правило, ограничивается нахождением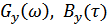 
и, соответственно, 
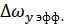и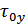 
.
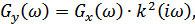
а, зная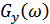 
, легко найти 
:
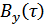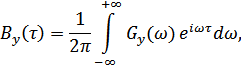
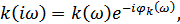
где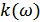 
и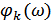 
– амплитудно-частотные и фазо-частотные характеристики соответственно.
Рассмотрим линейную инерционную систему, импульсная реакция которой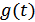 
и коэффициент передачи 
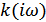известны и связаны между собой преобразованием Фурье.
Временное представление:
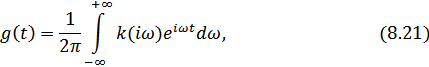
спектральное представление:
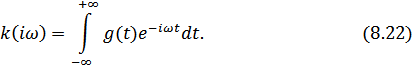
На вход системы поступает стационарный случайный сигнал 
с заданными характеристикам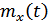и 
и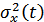 
. На выходе системы получаем некоторый случайный сигнал 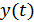. Согласно теореме Дюамеля:
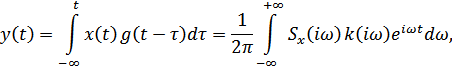
где
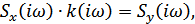
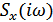– комплексный спектр отклика .
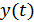В реальном четырехполюснике 
при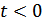 
(в силу принципа причинности) и 
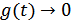при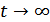 
(из-за наличия активных сопротивлений). Интервал времени, в котором сосредоточена основная часть энергии импульса реакции (рис. 8.19), будем называть временем памяти четырехполюсника:
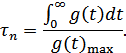
Рисунок 8.19. Графическое определение памяти четырехполюсника
где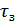 
– время задержки,
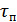– память четырехполюсника.
В большинстве четырехполюсников можно разделить полосы непропускания (где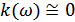 
) и пропускания. При наличии одной полосы пропускания его эффективная полоса определяется:
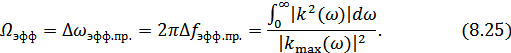
Принцип эквивалентного прямоугольника:
Рисунок 8.20. Графическое определение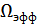 
четырехполюсника
Поскольку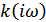 
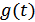и связаны между собой парой преобразования Фурье, то ширина полосы пропускания 
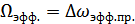и время памяти 
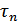четырехполюсника связаны обратно пропорциональной зависимостью:
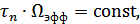
аналогично тому, как это имело место для эффективной полосы энергетического спектра и интервала корреляции случайного процесса.
Четырехполюсники, пропускающие энергию в полосе частот вблизи 
и имеющие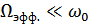 
( 
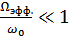), называют узкополосными. Их отклики – узкополосные сигналы. Если ширина полосы пропускания четырехполюсника 
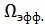намного уже ширины спектра воздействия 
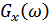, то имеет место так называемая нормализация случайного процесса.
При любом распределении воздействия и при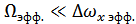 
отклик нормален и интервал корреляции отклика 
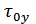оказывается много больше, чем 
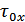воздействия (предельная теорема Ляпунова): 
.
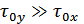Рисунок 8.21. Условие нормализации СП на выходе УПЛИЦ
8.8. Прохождение случайного сигнала через нелинейные безинерционные радиотехнические цепи
Рассмотрим теперь, как воздействует случайный сигнал на нелинейную систему. В общем случае это весьма трудная задача. Дело обстоит значительно легче, когда речь идет об безинерционных нелинейных системах, в которых выходной сигнал 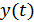в данный момент однозначно определяется входным сигналом в тот же момент времени.
Пусть известна характеристика нелинейного устройства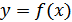 
и статистические свойства входного сигнала 
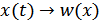. Необходимо определить статистические свойства выходного сигнала 
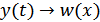. В принципе, эта задача сводится к преобразованию переменных.
Рассмотрим простейший случай одномерной плотности вероятности случайной величины. Плотность вероятности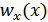 
случайной величины 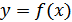известна.
Рисунок 8.22. Определение ФПВ СП на выходе НЭЦ через входные характеристики
Предположим, что существует однозначная обратная функция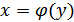 
. Т.к. случайные величины и 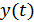связаны однозначной функциональной зависимостью, то из того, что 
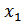заключено в достаточно малом интервале ( 
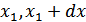) следует, что и 
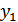будет находиться в интервале ( 
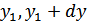), где 
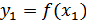, а сами вероятности равны произведению плотности вероятности на 
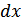или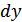 
.
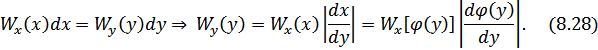
Поскольку плотности вероятностей не могут быть отрицательными, то в формулу (8.28) следует поставить модуль производной.
Далее можно найти числовые характеристики. Их легко вычислить через плотности вероятностей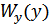 
или через 
.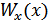