Функция (8.1) случайная, поэтому удобно ввести неслучайную функцию – энергетический спектр.

Дата: 2025-06-02; Просмотры: 17
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Энергетический спектр стационарного случайного процесса определяется как спектр его функции корреляции.

Прямое преобразование Фурье:

 

 

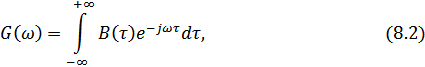
Обратное преобразование Фурье:

 

 

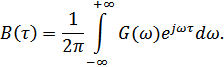
Пара преобразований, связывающая функци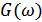и и 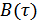, носит наз­вание преобразование (теорема) Винера-Хинчина. Т.к. 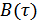и 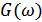– четные функции своих аргументов, то формулы можно записать в другом виде:

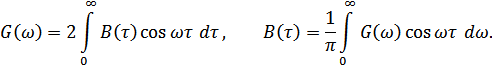
Физический смысл функции 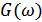легко выяснить, если положить 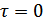, то­гда

 

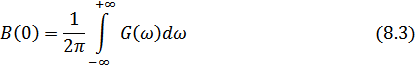
или

 

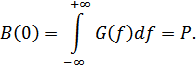
где 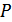– полная мощность процесса.

Поэтому энергетический спектр часто называют спектром мощности СП.

Формула (8.2) показывает, что функция 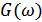выражает спектральную плот­ность мощности процесса и, следовательно, имеет размерность 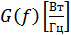, т.е. характеризует распределение мощности СП по частоте, это мощность СП в полосе частот 1 Гц.

Рисунок 8.2. Спектральная плотность мощности (энергетический спектр СП)

 

Мощность случайного процесса в полосе 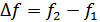или 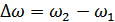определяется следующим образом:

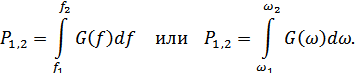
Энергетический спектр можно выразить через текущий спектр реализа­ции с помощью равенства Парсеваля: энергия сигнала определяется интегралом квадрата напряжения или интегралом квадрата модуля его спектральной плот­ности по частоте. Энергия процесса 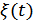, выделяющегося за время 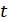, равна:

 

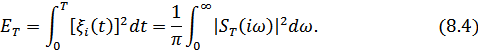
Средняя мощность процесса определяется как предел 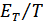при 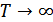, т.е.

 

 

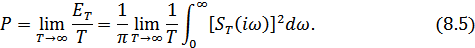
Сопоставляя (8.4) и (8.3), находим:

 

 

Это соотношение устанавливает связь между энергетическим спектром процесса и текущим спектром его реализации.

 

 

8.2. Узкополосные и широкополосные случайные процессы. Белый шум

Энергетические спектры реальных процессов практически ограничены полосой частот 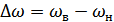, поэтому в дальнейшем удобно разделить случай­ные процессы на узкополосные и широкополосные, в зависимости от положе­ния 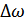на шкале частот. Случайный процесс с непрерывным энергетическим спектром (в частности с равномерным) называется узкополосным, если энерге­тический спектр процесса сосредоточен в основном в относительно узкой по­лосе частот, около некоторой средней частоты , или широкополосным, если указанное условие не выполняется.

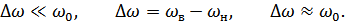
Рисунок 8.3. Энергетические спектры

а) узкополосного СП;

б) широкополосного СП

Условие узкополосности обычно выражается неравенством .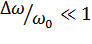

Случайный процесс, у которого спектральная плотность мощности оди­накова на всех частотах, называется «белым» шумом (по аналогии с белым све­том, имеющим сплошной и равномерный спектр в пределах видимой части спектра). Функция спектральной плотности белого шума 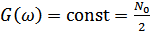, где 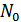– спектральная плотность, представленная на рис. 8.4.

Отметим, что мы пользуемся представлением спектра на всей оси частот 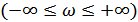. Этот спектр является симметричным относительно частоты .

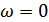Поэтому спектральная плотность в наших обозначениях в два раза меньше реальной спектральной плотности 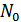, под которой понимается мощ­ность шума, приходящаяся на 1 Гц полосы частот, корреляционная функция белого шума, согласно (8.2):

 

 

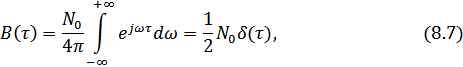
где

 

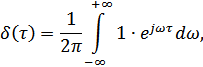
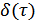– дельта функция.

Рисунок 8.4. Энергетический спектр «белого» шума

 

Таким образом, функция корреляции белого шума выражается функцией, показанной на рис. 8.5. Это означает, что сечения случайного процесса некор­релированы при любом сколь угодно малом временном сдвиге, т.е. интервал корреляции 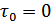, поэтому белый шум называют «чисто» (абсолютным) СП.

Рисунок 8.5. Функция корреляции «белого» шума

 

 

8.3. Эффективная ширина энергетического спектра и ее связь с ин­тервалом корреляции

При описании случайных процессов с неравномерным энергетическим спектром, интенсивность которого убывает с ростом частоты, пользуются по­нятием эквивалентной или эффективной ширины энергетического спектра.

Рисунок 8.6. Графическое определение ширины спектра СП

а) широкополосный СП;

б) узкополосный СП

 

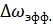– это та полоса частот, в пределах которой сосредоточена основ­ная мощность СП, определяется по 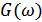по правилу эквивалентного прямоуголь­ника с высото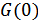й (или 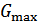) и таким основанием 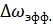, при кото­ром площадь эквивалентного прямоугольника равна площади под кривой 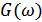. Аналогично определяется и интервал корреляции .

 

 

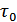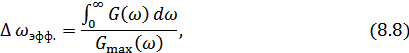
где 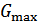– наибольшее значение функции.

С учетом взаимосвяз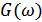и и 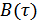величину 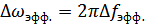можно связать с интервалом корреляции на основе соотношения .

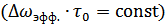Рисунок 8.7. Графическое определение интервала корреляции СП ( )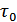

 

 

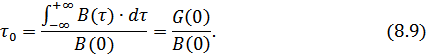
При :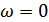

 

 

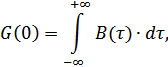
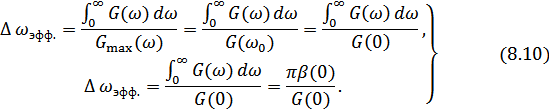
В (8.10) учтено, что при 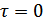из (8.2):

 

 

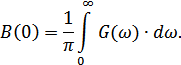
Тогда:

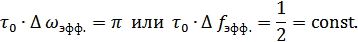
Рисунок 8.8. Графическая иллюстрация постоянства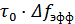

 

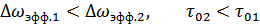
Если временные функции имеют следующий вид:

Рисунок 8.9. Временное представление:

а) широкополосного СП;

б) узкополосного СП

 

то 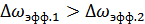, т.к. функция 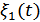изменяется быстрее, чем .

 

 

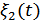8.4. Функция корреляции узкополосного случайного процесса

 

Рисунок 8.10. Сущность определения функции корреляции узкополосного СП

Смещая спектр 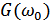влево на , получим спектр узкополосного про­цесса через широкополосный. Функция автокорреляции узкополосного процесса выражается формулой:

 

 

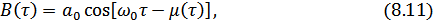
где 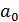и 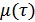– медленно меняющиеся функции, соответствующие ампли­туде и фазе функции корреляции. Скорость изменения этих функций прямо пропорциональна изменению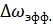

Для вывода этой формулы производят замену переменной 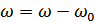. Но мы не будем этого делать. Раскрывая в (8.11) косинус суммы, получаем:

 

 

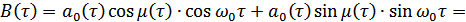
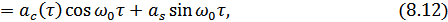
т.е. функция автокорреляции узкополосного СП равна сумме 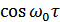и 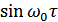, взятых с коэффициентами .

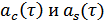Особый интерес представляет функция 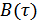, когда 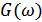симметричен отно­сительно . В этом случае 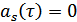, т.к. .

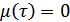Тогда:

 

 

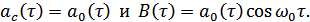
Но 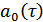– функция автокорреляции, и она может быть вычислена через 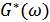, т.е. через спектр, сдвинутый влево на .

 

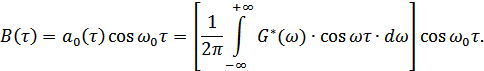
Рисунок 8.11. Энергетический спектр и функция корреляции СП, сдвинутого на

Рисунок 8.12. Графическое определение интервала корреляции 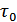узкополос­ного СП

 

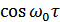Таким образом, функция автокорреляции узкополосного СП, спектр ко­торого симметричен относительно , равна умноженной на корреляци­онной функции 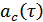, которая соответствует спектру 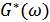, получен­ному из исходного смещением влево на величину .

 

 

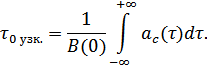
Интервал корреляции узкополосного СП определяется по огибающей :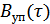

 

 

 

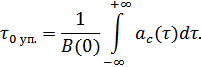
8.5. Функция корреляции «белого» шума, ограниченного полосой час­тот от 0 до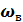

 

Рисунок 8.13. Энергетический спектр «белого» шума, ограниченного

 

Если «белый» шум с равномерным энергетическим спектром пропустить через идеальный ФНЧ с граничной частотой 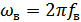, то и на выходе получим шум с ограниченным спектром (рис. 8.13), причем ширина спектра 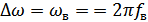. Для определения функции корреляции воспользуемся соотношением:

 

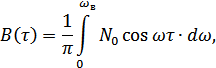
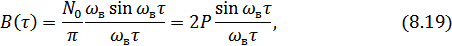
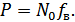
Таким образом, график 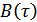имеет вид функции .

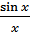Рисунок 8.14. Функция корреляции «белого» шума, ограниченного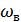

 

График корреляционной функции приведен на рис. 8.14.

При данном виде график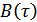а за 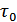можно принять 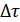между двумя пер­выми нулями, т.е. 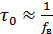. Из этого соотношения видно, что по мере сокращения полосы частот 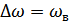, интервал корреляции увеличивается. ограничение спек­тра влечет за собой усиление корреляции между сечениями СП.

 

 

8.6. Функция корреляции «белого» шума, ограниченного полосой час­тот от 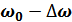до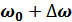

 

Пусть энергетический спектр равномерен в полосе частот 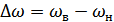и равен 0 на всех других частотах.

 

 

 

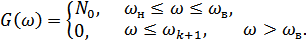
Это случай идеального полосового фильтра.

Рисунок 8.15. Энергетический спектр «белого» шума, ограниченного иде­альным ПФ

 

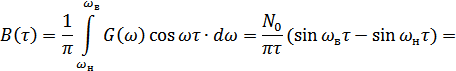
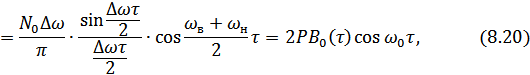
где:

 

 

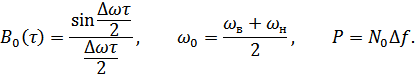
По формуле (8.20) построен график (рис. 8.16).

Огибающая функции (8.20) имеет ту же форму, что и корреляционная функция соответствующего по полосе широкополосного процесса (8.19). Со­поставляя (8.20) и (8.19), а также рисунки 8.15 и 8.16, можно сказать следую­щее: для построения корреляционной функции узкополосного процесса доста­точно найти корреляционную функцию огибающей широкополосного процесса и вписать в нее косинусоидальное заполнение с частотой, равное средней час­тоте процесса.

Рисунок 8.16. Функция корреляции «белого» шума, ограниченного идеальным ПФ

8.7. Прохождение случайных процессов через линейные инерцион­ные радиотехнические цепи

 

1. Классификация радиотехнических цепей.